Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Ground Motion Prediction Equations (GMPEs)
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Today, we’ll look into Ground Motion Prediction Equations, often referred to as GMPEs. These equations help us estimate Peak Ground Acceleration, or PGA, which is essential for seismic design. Can anyone tell me why PGA is important?
I think it's because it helps in designing buildings to withstand earthquakes.
Exactly! It provides a basis for designing structures to minimize seismic risk. The basic formula we use is: log(PGA) = a + bM - c log(R + d). Does anyone know what M and R stand for?
M is the magnitude of the earthquake, and R is the distance from the earthquake epicenter.
Correct! Understanding these variables is crucial for predicting how severe ground shaking will be. Let's remember: M for Magnitude and R for Distance. We can represent these with the mnemonic 'Magnitude Matters'!
Significance of Empirical Constants in GMPEs
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now, let’s dive deeper into the empirical constants in GMPEs. Can anyone tell me what role these constants play?
They are likely used to fit the model to historical data or something like that.
Yes, very good! Each constant represents how PGA changes with respect to magnitude and distance, allowing us to tailor predictions for different tectonic settings. For instance, we have different models based on whether we're dealing with subduction zones or intraplate regions.
So, they help in making the predictions more accurate?
Exactly! Knowing the geological context is crucial. Remember, constants calibrate our model, making it more reliable. Thank you for sharing those insights!
Application of GMPEs in Seismic Design
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
How do we think GMPEs are applied in real-world scenarios, particularly in seismic risk assessment?
I believe engineers use them to assess how buildings will perform during an earthquake, right?
Yes! They help engineers design structures that can handle specific levels of PGA based on their location. By estimating PGA through GMPEs, we can create better building codes and guidelines.
And that means we can reduce potential damage and save lives?
Precisely! Using these equations allows for informed decisions that can protect both property and human life. Remember, proper estimates lead to strong designs!
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In this section, we explore how PGA is estimated through empirical relationships known as Ground Motion Prediction Equations (GMPEs). The section details the mathematical formulation and explains how different constants are derived based on various tectonic settings, enhancing the understanding of seismic assessments.
Detailed
Empirical Relationships and Attenuation Models
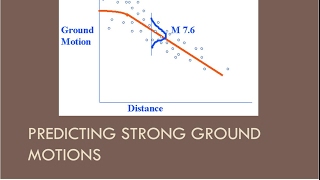
This section explains the estimation of Peak Ground Acceleration (PGA) using Ground Motion Prediction Equations (GMPEs), which are crucial for assessing seismic hazards. The GMPEs relate PGA to two primary variables: earthquake magnitude (M) and hypocentral/epicentral distance (R).
Key Equation
The general form of the GMPE is:
log (PGA) = a + bM - c log (R + d)
Where:
- M = magnitude of the earthquake
- R = hypocentral or epicentral distance
- a, b, c, d = empirical constants determined through historical earthquake data.
Different GMPEs exist tailored for varying tectonic environments, such as subduction zones and intraplate regions. These models help engineers and scientists predict how strong the ground shaking will be at different distances from the earthquake source, thus ensuring safer structural design and risk assessments.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Ground Motion Prediction Equations (GMPEs)
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
PGA is commonly estimated using Ground Motion Prediction Equations (GMPEs) of the form:
log (PGA)=a+bM−clog (R+d)10
where:
- M = magnitude
- R = hypocentral/epicentral distance
- a, b, c, d = empirical constants
Detailed Explanation
Ground Motion Prediction Equations (GMPEs) are mathematical formulas used to estimate the expected Peak Ground Acceleration (PGA) during an earthquake. The equation shown breaks down as follows:
1. Logarithmic Relationship: The equation uses a logarithmic scale, which helps in capturing the wide range of potential values of PGA.
2. Variables Explained:
- M (Magnitude): This reflects the size of the earthquake; larger magnitudes typically yield higher accelerations.
- R (Distance): This is either the hypocentral or epicentral distance from the earthquake source to the measuring site. PGA generally decreases as you move further from the epicenter.
- Constants (a, b, c, d): These are empirical constants determined through analysis of historical earthquake data, helping to calibrate the model based on observed ground motions.
3. Usage: Engineers and seismologists use GMPEs to predict how strong the shaking will be at various distances for different magnitudes, informing the design and safety of structures in earthquake-prone areas.
Examples & Analogies
Think of GMPEs like a weather forecast. Just as meteorologists use data from past weather patterns, temperature, and atmospheric conditions to predict future weather events, seismologists use past earthquake data to predict how much ground shaking will occur in future quake scenarios based on size and distance.
Variability of GMPEs Across Tectonic Settings
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Different models exist for different tectonic settings (e.g., subduction zones, intraplate regions).
Detailed Explanation
In earthquake engineering, it’s important to recognize that the behavior of seismic waves can change depending on the geological and tectonic context.
1. Tectonic Settings: Areas of the Earth's crust can be classified broadly by their tectonic activity. Two significant types are:
- Subduction Zones: Where one tectonic plate moves under another, often resulting in very strong earthquakes.
- Intraplate Regions: Areas located within a tectonic plate, which usually have different seismic characteristics compared to fault lines.
2. Model Variability: Due to these differences, GMPEs are tailored or adjusted based on these settings to make their predictions more accurate. For example, a GMPE used for predicting shaking in a subduction zone will likely account for the characteristics of deep, powerful earthquakes that are not applicable in intraplate regions, where shocks might be weaker and closer to the surface.
Examples & Analogies
Consider driving down different types of roads. For instance, driving on a highway (subduction zone) requires different car handling than on a bumpy dirt road (intraplate region). Just as you adjust your speed and strategy based on road conditions, seismologists adapt GMPEs based on geological environments to accurately predict how an earthquake will affect the ground.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
GMPE: Ground Motion Prediction Equations are the formulas used to estimate PGA based on earthquake characteristics.
-
Variables: M (magnitude) and R (distance) are essential inputs for estimating PGA using GMPEs.
-
Empirical Constants: These values (a, b, c, d) calibrate the GMPEs to fit historical data.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
If an earthquake has a magnitude of 7.0 and is located 10 km away from a structure, GMPEs can help predict the expected PGA at that location.
-
In a soft soil region, GMPEs will likely yield a higher estimated PGA due to increased ground motion amplification compared to rocky areas.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Magnitude and distance, we must consider, for PGA’s prediction, it’s the best critter.
📖 Fascinating Stories
-
Imagine a wise old engineer who always checks the distance and strength of earthquakes before building, ensuring safety through GMPEs.
🧠 Other Memory Gems
-
Mighty Raging Giants: M for Magnitude, R for Distance, G for GMPE, reminding us of the three main elements.
🎯 Super Acronyms
For MAG R
- Magnitude
- Attenuation
- Geology
- R: for Distance - this sums up the GMPE variables.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Peak Ground Acceleration (PGA)
Definition:
The maximum acceleration experienced by the ground during an earthquake, typically measured in g or m/s².
-
Term: Ground Motion Prediction Equations (GMPEs)
Definition:
Empirical relationships used to estimate ground shaking based on earthquake magnitude and distance to the source.
-
Term: Epicentral Distance
Definition:
The distance from the earthquake's epicenter to the site of interest.