Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Lateral Forces
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Today, we'll discuss how we calculate lateral forces at different storeys of a building. Does anyone know why we need to calculate these forces?
I think they help us understand how much stress each floor experiences.
Exactly, stress on the structure is vital to its stability during seismic events. We express the lateral force at each storey using the formula Qᵢ = (Vᵦ * Wᵢ * hᵢ²) / ∑(Wᵢ * hᵢ²). Can someone tell me what each part represents?
I think Vᵦ is the base shear and Wᵢ is the weight of that storey, right?
Yes, correct! And hᵢ is the height of the storey from the base. This formula ensures that we distribute the forces based on the relative height and weight of each floor. Let me give you a memory aid: Think of the word 'WEIGHT' — it hints at weight and how force is distributed by height.
So the higher the storey, the more force it receives?
That's right, because the forces are proportional to the square of the height. Now, can someone summarize the importance of understanding this calculation?
It's essential for ensuring the structure's safety and performance during an earthquake!
Exactly! Safety is our number one priority. Let's review that: the formula calculates lateral forces based on storey weight and height, crucial for seismic design.
Storey Shear and Overturning Moment
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now let's look at storey shear and how it relates to overturning moments. Any initial thoughts on what storey shear means?
Is it the total lateral force acting at a particular storey?
Good point! Storey shear is indeed the total lateral force experienced at any floor level, considering all forces above it. This understanding is crucial because it helps us calculate the overturning moment, which is influenced by the height at which these forces act. Can someone explain why this is significant?
If we know the overturning moment, we can design the structure to prevent it from tipping over.
Exactly! The overturning moment is calculated as the product of lateral force and vertical distance. This allows engineers to ensure stability. Remember: 'STABILIZED' for stabilizing forces against overturning. Can anyone give an example of how we ensure stability in a design?
We can use techniques like adding shear walls or bracing.
Great example! So remember, calculating storey shear and overturning moments helps us determine how to reinforce structures effectively to withstand seismic forces.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
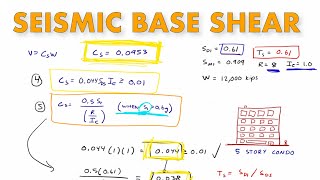
In this section, the vertical distribution of base shear is explored along with the associated lateral forces on each storey of a structure. The calculations involve seismic weight and height that form the basis of lateral load distribution, vital for structural integrity during an earthquake.
Detailed
Vertical Distribution of Base Shear
Understanding the vertical distribution of base shear is crucial for earthquake-resistant design. The lateral force at each storey is determined using the formula:
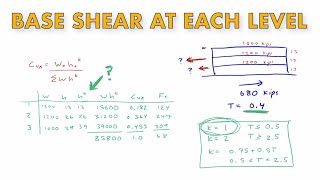
Qᵢ = (Vᵦ * Wᵢ * hᵢ²) / ∑(Wᵢ * hᵢ²)
Where Qᵢ represents the lateral force applied to floor i, Wᵢ is the seismic weight of that floor, hᵢ is the height from the base to that floor, summed across all floors in the structure. This approach ensures that the lateral forces are appropriately calculated based on the dynamic behavior of the structure under seismic loads, helping to assess both storey shear and overturning moment. The understanding of these forces is necessary for engineers to design structures that can withstand significant seismic events with minimal damage, ensuring both safety and functionality.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Lateral Force at Each Storey
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Lateral Force at Each Storey (IS 1893)
Q = \[ V_b \cdot \frac{W_i h^2_i}{\sum W_i h^2_i} \]
Where:
- Q : Lateral force at floor i
- W : Seismic weight of floor i
- h : Height of floor i from base
Detailed Explanation
In seismic design, the lateral force (Q) acting on each storey of a building is calculated using a formula. This formula considers the weight of each floor (W_i) and the height of that floor (h_i) from the base. The lateral forces are proportional to the weight and height of each floor, which means heavier and higher floors will experience more force during an earthquake. The total base shear (V_b) is distributed to the floors based on their relative stiffness and height, leading to a more even distribution of lateral forces throughout the building.
Examples & Analogies
Imagine a stack of books on a table. The heavier books at the bottom apply more pressure and experience more force when the table shakes. Similarly, in a building, the higher and heavier floors will feel the impact of an earthquake more significantly, and this is accounted for by the formula to ensure the structure is designed to handle these forces.
Storey Shear and Overturning Moment
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Storey Shear and Overturning Moment
- Storey shear: Sum of lateral forces above the level.
- Overturning moment: Based on lateral forces and vertical distances.
Detailed Explanation
Storey shear is the total lateral force acting on a given floor from all the floors above it. This shear force is crucial for understanding how much force each storey experiences, which informs engineers how the building will behave under earthquake conditions. The overturning moment refers to the tendency of the building to tip over due to these lateral forces, calculated based on the lateral force and the height (or vertical distance) from the base to the center of mass of the affected structure. Engineers must ensure that the design can resist these moments to prevent failure.
Examples & Analogies
Think of a tall bookshelf with several shelves. If you push it sideways, the force at the top has a greater 'lever' arm effect, making it easier for the shelf to tip over. The bookcase's bottom shelves experience the combined weight and forces from the shelves above, which is similar to how storey shear and overturning moments interact in a building during an earthquake.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Vertical Distribution of Base Shear: Understanding how base shear is distributed across different storeys.
-
Lateral Force Formula: The calculation method for determining lateral forces per storey.
-
Storey Shear: Total lateral forces experienced by a specific storey based on the forces above it.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
If a building has 4 storeys with a total seismic weight of 200 kN, the distribution of forces can be calculated assuming heights are different for each storey.
-
For example, if the second storey is located 3 meters above the base and has a weight of 50 kN, it would experience lateral forces proportional to its height squared.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Lateral forces sway, storey shear plays, keep structures intact, in quakes they won't lack.
📖 Fascinating Stories
-
Imagine a tall tower swaying when the ground shakes; each floor must hold its weight, or it would break!
🧠 Other Memory Gems
-
To remember 'Qᵢ,' think of 'Quick Impact' since it represents lateral force on each storey.
🎯 Super Acronyms
LFS—Lateral Force Stability—to remember the importance of calculating lateral force for stability.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Lateral Force
Definition:
A force that causes a structure to sway sideways during seismic activity.
-
Term: Storey Shear
Definition:
The sum of lateral forces acting on the floors above a specific level.
-
Term: Overturning Moment
Definition:
A moment that tends to cause a structure to rotate or tip over, calculated using lateral forces and distances.