Conditional Mean Spectrum (CMS)
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Conditional Mean Spectrum
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today we will focus on the Conditional Mean Spectrum or CMS, which is an innovative method in earthquake engineering. Can anyone tell me what a standard Uniform Hazard Spectrum does?

It gives a general idea of how buildings should respond to earthquakes over time.

Exactly! UHS provides a uniform measure across various periods. But CMS goes further. It conditions the spectrum on specific factors. Like, what do you think those specific factors could be?

Maybe it depends on the type of building or its location?

Correct! CMS is particularly crucial for structures with significant responses at tailored periods. This leads us to a fundamental question: why is specificity in a response spectrum important?

It likely helps to make the designs more accurate and less conservative.

Exactly! By conditioning on the response at specific periods, we are addressing the unique characteristics of a site and a given structure, improving design accuracy.

In summary, CMS enhances the predictability of seismic responses for specific structures, helping engineers make better-informed design decisions.
Applications of CMS
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now that we understand what CMS is, let’s discuss its applications. Who can think of a scenario where CMS would be particularly useful?

For example, in designing tall buildings or bridges that are particularly sensitive to seismic activities?

Exactly, structures like tall buildings or bridges, especially those that have long fundamental periods, can significantly benefit from CMS. Would anyone like to explain why this is the case?

Because those structures might sway more and need to have an accurate measurement at their specific response periods?

Great point! CMS focuses on periods where non-linear behavior is prevalent, ensuring that we capture the essential dynamic effects impacting the structure. Let’s summarize today’s session: CMS provides tailored spectral responses based on specific periods, reducing conservatism in designs.
CMS vs. UHS
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

To enhance our understanding of CMS, let's compare it with Uniform Hazard Spectrum. What are some fundamental differences you think exist between the two?

I believe UHS might be overly conservative for some structures.

Absolutely! UHS applies a uniform risk approach, which may not always suit every building's requirement. Why do you think that could affect engineering decisions?

Engineers might end up designing structures that overestimate their needed strength, leading to higher costs.

Precisely! By providing a more realistic representation of seismic risks, CMS encourages efficient designs and resource utilization. Let's recap: CMS's specificity helps in applying realistic data to assist structural engineering in real scenarios.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
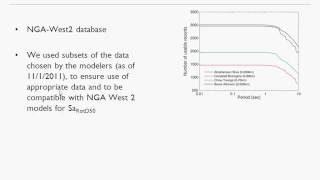
CMS is positioned as an alternative to the Uniform Hazard Spectrum (UHS) in earthquake engineering, particularly beneficial in nonlinear time history analysis. It emphasizes accuracy by conditioning on significant spectral accelerations at specific periods, particularly in dominating nonlinear structural behaviors.
Detailed
Conditional Mean Spectrum (CMS)
The Conditional Mean Spectrum (CMS) serves as a significant alternative to the traditional Uniform Hazard Spectrum (UHS) utilized in earthquake engineering. Unlike UHS, which provides a generic approach by representing spectral accelerations uniformly across periods for a fixed probability, CMS presents a more tailored response spectrum conditioned on specific site and structural characteristics.
Key Features of CMS:
- Specificity: CMS zeroes in on the occurrence of a spectral acceleration at a targeted period, usually the fundamental period of the structure.
- Application: It is especially relevant in nonlinear time history analysis where structures predominantly respond to motions at particular periods, thus addressing the limitations of UHS.
- Reduced Conservatism: By focusing on dominant responses, CMS mitigates the over-conservatism often seen in UHS, making it a vital tool for engineers designing structures subjected to varied seismic inputs.
Overall, CMS is pivotal in enhancing the reliability and development of structures, particularly in regions with specific seismic challenges.
Youtube Videos




![[BCT2025 Webinar] Long Period Ground Motion in Earthquake – its Impacts, Measures and Effects 1](https://img.youtube.com/vi/0lGZlFHEbS4/mqdefault.jpg)


Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to CMS
Chapter 1 of 2
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
• Alternative to UHS, CMS provides more realistic response spectra.
• Conditioned on occurrence of a specific spectral acceleration at a period of interest (typically the fundamental period of the structure).
Detailed Explanation
The Conditional Mean Spectrum (CMS) is presented as an alternative to the Uniform Hazard Spectrum (UHS). While UHS gives a general view of possible seismic response, it may not accurately reflect the actual behavior of structures under seismic loads. CMS, on the other hand, is generated based on specific criteria, focusing on particular spectral accelerations at key periods, notably the fundamental period of the structure. This targeted approach results in a more accurate representation of expected seismic responses, tailored to the nuances of a given structure's dynamics.
Examples & Analogies
Think of the CMS like a tailored suit. Just as a custom suit is designed to fit the unique dimensions and style preferences of an individual, the CMS is designed to fit the specific seismic behaviors of a structure, ensuring a better fit compared to a one-size-fits-all solution like the UHS.
Application of CMS
Chapter 2 of 2
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
• Nonlinear time history analysis where response at specific period dominates.
• Reduces over-conservatism seen in UHS for longer period structures.
Detailed Explanation
The CMS is particularly valuable during nonlinear time history analyses, which are used to simulate how structures respond to actual earthquake ground motions. In these analyses, it is essential to focus on the periods that significantly influence the structure's behavior, which is often the fundamental period. This focus helps mitigate the excessive conservatism that may arise from using the UHS, especially for structures that can exhibit longer response periods. By integrating CMS into analyses, engineers can achieve a more realistic assessment of structural performance during seismic events.
Examples & Analogies
Consider a cyclist adjusting their bike's gears depending on the terrain. In hilly areas, they might choose lower gears for better control and safety. Similarly, CMS tailors the seismic analysis for longer period structures, allowing engineers to avoid overly conservative approaches that might impose unnecessary design constraints.
Key Concepts
-
Conditional Mean Spectrum: A tailored spectrum based on specific spectral accelerations.
-
Nonlinear Time History Analysis: An approach assessing seismic responses under real conditions over time.
Examples & Applications
Using CMS for a tall building in a seismic-prone area to prevent over-designing while ensuring safety.
Implementing CMS in analyzing long-span bridges to capture their unique dynamic behavior.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
In the land of quakes where buildings sway, CMS helps in a precise way.
Stories
Imagine a tall tower that wobbles with the tremors. Instead of guessing how strong the winds should be, CMS whispers, 'Look at how it sways' and saves the day.
Memory Tools
Remember 'CMS' as 'Customized Measure for Structures'.
Acronyms
CMS
Conditional Measurement Spectrum for Specificity.
Flash Cards
Glossary
- Conditional Mean Spectrum (CMS)
A response spectrum conditioned on a specific spectral acceleration, offering a tailored representation of seismic responses.
- Uniform Hazard Spectrum (UHS)
A spectrum that provides a uniform measure of ground motion characteristics across various periods for a fixed probability.
Reference links
Supplementary resources to enhance your learning experience.
