Correlations in Mass Transfer
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Sherwood Number
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today, let's discuss the Sherwood number, or NSh. The Sherwood number is essential because it relates mass transfer by convection and diffusion. Can anyone recall how it's calculated?

Isn't it kA multiplied by a length scale divided by the diffusion coefficient?

Exactly! You’ve got it. The formula is NSh = kA * L / D. Here, L represents the characteristic length of the system. Can anyone think of examples where we use NSh?

What about when measuring mass transfer in lakes or rivers?

Yeah, and during oil spills too! The Sherwood number helps us understand the rate at which contaminants diffuse.

Right! Always remember that NSh signifies the strength of mass transfer in environmental contexts.

So, in summary, the Sherwood number is integral to evaluating mass transfer, especially in environmental applications.
Reynolds Number Insights
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Let's move on to the Reynolds number. Who can tell me what it indicates?

It's the ratio of inertial forces to viscous forces in a fluid.

Correct! And it’s calculated as NRe = (velocity * length) / viscosity. This means that higher velocities lead to larger Reynolds numbers, indicating more turbulent flow. Why is turbulence important?

Turbulence enhances mixing and increases mass transfer rates!

Exactly! Higher turbulence means better convective transfer. However, it’s vital to apply the same length scale consistently when using NRe and NSh - they are interconnected.

To wrap up, the Reynolds number helps predict flow behaviors. Remember to always define dimensions clearly!
Schmidt Number and Its Applications
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now let's discuss the Schmidt number, NSc. Does anyone know what it represents?

Isn’t it the ratio of momentum diffusivity to mass diffusivity?

Exactly! NSc = viscosity / (density * diffusion coefficient). It helps us understand how mass transfer varies in different liquids. Why do we care about this in environmental science?

Because different substances will diffuse at varying rates, affecting pollution spread!

Exactly! Knowing how to apply these numbers is crucial, especially in pollution scenarios.

So in conclusion, the Schmidt number informs us about mass transfer dynamics in different environments, helping us predict pollutant behavior.
Practical Applications and Case Studies
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Let’s wrap up by discussing some practical applications. How do these numbers correlate to real-world scenarios, such as an oil spill?

In oil spills, understanding NSh helps us know how fast oil spreads while NRe helps us assess the mixing effect of water currents.

Absolutely! Each dimensionless number plays a critical role in predicting the fate of pollutants. Can anyone mention any specific correlations?

There are correlations for lakes, rivers, and even wind-induced turbulence!

Correct! These correlations provide experimental insights into mass transport in various aquatic environments. Therefore, understanding them enhances our risk assessments.

To sum it up, these correlations guide environmental scientists in successfully managing pollution.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
The section elaborates on the significance of dimensionless numbers such as the Sherwood number for understanding mass transfer, explaining how these numbers correlate convective and diffusive mass transport in fluid systems. It emphasizes the need for precise definitions and measurements in experimental settings, especially concerning environmental interactions.
Detailed
Correlations in Mass Transfer
In this section, we delve into the significance of dimensionless numbers in the study of mass transfer, highlighting the Sherwood (NSh), Reynolds (NRe), and Schmidt (NSc) numbers. These correlations provide critical insights into how mass is transferred between phases, especially in the context of environmental applications.
1. Sherwood Number (NSh): The Sherwood number is a dimensionless quantity given by the formula NSh = kA * L/D, where kA represents the mass transfer coefficient, L is a characteristic length, and D is the diffusion coefficient. This number helps in understanding the ratio of convective mass transport to diffusive mass transport.
2. Reynolds Number (NRe): Defined as NRe = (velocity * length) / viscosity, it indicates the ratio of inertial forces to viscous forces in the fluid. A higher Reynolds number suggests higher turbulence, which enhances mass transfer rates. It is crucial to maintain consistency in defining length scales across different calculations.
3. Schmidt Number (NSc): The Schmidt number is defined as NSc = viscosity / (density * diffusion coefficient). It characterizes the relative thickness of the momentum and mass diffusion boundary layers.
Applications and Environmental Considerations: The section includes various specific correlations for different environmental scenarios, such as wind-induced turbulence in water bodies, temperature gradients in lakes, and mass transfer coefficients at air-water interfaces or sediment interfaces. The significance of accurate measurements and definitions in experimental correlations is crucial, as demonstrated in common problems such as oil spills in aquatic environments.
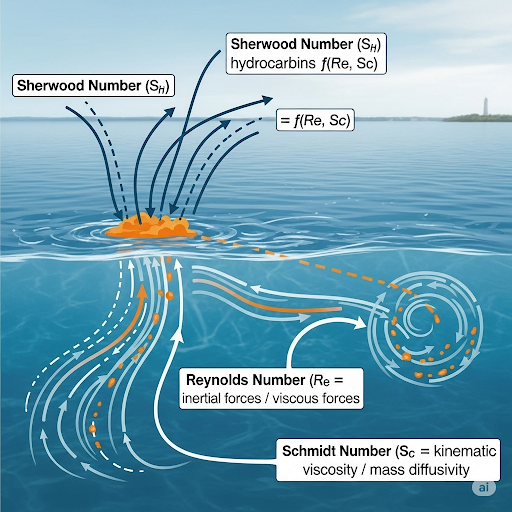
Overall, understanding these dimensionless numbers and their applications not only highlights the foundational theories of mass transfer but also equips students with the knowledge to address real-world environmental challenges.
Youtube Videos










Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Dimensionless Correlations
Chapter 1 of 6
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
A good correlation is usually a dimensionless correlation. This has a lot of advantages in terms of the units that we use.
Detailed Explanation
Dimensionless correlations are essential because they provide a way to compare different systems without being influenced by the specific units of measurement. For instance, when measuring mass transfer coefficients, using dimensionless numbers such as the Sherwood number allows engineers to understand mass transfer behavior in various scenarios without confusion from unit conversions. These correlations are universally applicable across different scales and systems, making them highly valuable in engineering.
Examples & Analogies
Think of dimensionless correlations like a universal language for travelers. Just as a traveler can communicate effectively with locals around the world using simple phrases and gestures rather than complex translations of their native tongue, engineers use dimensionless correlations to communicate and understand mass transfer phenomena without getting bogged down in the specifics of different measurement systems.
Understanding the Sherwood Number (NSh)
Chapter 2 of 6
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
The Sherwood number (NSh) is defined as a mass transfer coefficient multiplied by some dimensional parameters. NSh = α [L / D]^m [D]^n [H].
Detailed Explanation
The Sherwood number is a key dimensionless number in mass transfer, representing the ratio of convective mass transport to diffusive mass transport. It is used to analyze how effectively a substance moves through a medium. The variables in the formula—α, L, D, and H—represent specific physical parameters such as the mass transfer coefficient (α), length scale (L), diffusion coefficient (D), and possibly others that account for different conditions or setups. Understanding this number helps in predicting how substances will behave when they interact across different phases, like liquid to gas.
Examples & Analogies
Consider the Sherwood number as a traffic report for a city. Just as a traffic report gives us an insight into whether vehicles are moving quickly (convective transport) or slowly (diffusive transport) in different areas of the city, the Sherwood number gives engineers insight into how fast or slow a chemical moves through a system, helping them design better processes and systems.
Reynolds Number (Re)
Chapter 3 of 6
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
The Reynolds number (Re) is defined as Re = (Inertial forces)/(Viscous forces) and is indicative of the flow regime of the fluid.
Detailed Explanation
The Reynolds number quantifies the relationship between inertial and viscous forces within a fluid. A high Reynolds number (typically >2000) indicates turbulent flow, where fluid behavior is chaotic, whereas a low Reynolds number indicates laminar flow, where the fluid moves in smooth layers. This number is crucial in predicting how a fluid will behave in different scenarios, affecting mass transfer rates significantly.
Examples & Analogies
Imagine a busy highway (high Re) versus a quiet country road (low Re). On the highway, cars don’t just follow each other in a straight line; they change lanes, speed up, and slow down, creating turbulence. On the country road, cars move more predictably, one behind the other, creating a smooth flow. In the same way, in fluid dynamics, these flow patterns will dictate how substances mix and transfer—turbulence enhances mixing while laminar flow restricts it.
Schmidt Number (Sc)
Chapter 4 of 6
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
The Schmidt number (Sc) is defined as Sc = (Kinematic Viscosity)/(Diffusion Coefficient) and helps to characterize mass transfer.
Detailed Explanation
The Schmidt number connects the momentum diffusion (viscosity) with mass diffusion (substance transport) in a fluid. It provides insights into whether viscous forces or diffusive forces dominate the transport process. A low Schmidt number indicates that mass diffusion rates are high relative to viscous forces, which is often seen in gases, while a high Schmidt number indicates dominant viscous effects, common in liquids. This understanding can help optimize systems for chemical reactions and separations.
Examples & Analogies
Think of the Schmidt number as a dance competition. In a team that dances fluidly and synchronously (a low Schmidt number), the movements synchronize smoothly, allowing the team to perform efficiently. Conversely, in a dance where people are clumsy and bump into each other (high Schmidt number), the performance is less coordinated and efficient. In this analogy, smooth movements signify the efficient transfer of mass, while clumsiness represents hindered transport due to external resistance.
Interdependence of Mass Transfer Parameters
Chapter 5 of 6
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
A good correlation takes into account everything; this means all factors are all there, which means significant experimental work has been put into deriving them.
Detailed Explanation
A robust correlation in mass transfer implies a comprehensive understanding of the interactions between different parameters, such as Reynolds number, Schmidt number, and the specific geometric dimensions of the system. When experiments are extensively conducted across various scenarios, they help in developing correlations that accurately reflect real-world behavior. Therefore, when using correlations, it is crucial to know that they are derived from specific experimental conditions and to ensure that these conditions apply to your specific scenario.
Examples & Analogies
This process can be likened to a restaurant menu that is developed after extensive customer feedback. Just as a chef uses reviews and data from various dining experiences to create dishes that satisfy most patrons, engineers rely on empirical data to formulate correlations that comprehensively represent mass transfer processes, ensuring reliable results in various applications.
Geometric Considerations in Correlations
Chapter 6 of 6
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
The length scale (L) used in correlations must match in both Reynolds and Sherwood numbers for accurate application.
Detailed Explanation
When performing calculations involving mass transfer coefficients, ensuring that the geometric length scales used in different dimensionless numbers (like Reynolds and Sherwood) match is crucial. For example, if one correlation uses the diameter of a particle while another uses the length of a river segment, mismatched parameters could lead to inaccurate results. It’s essential to be consistent and to understand which dimensions are relevant for specific calculations.
Examples & Analogies
Imagine measuring the height of a building with two different tapes: one tape shows inches while the other shows centimeters. If you compare the measurements from both tapes without converting the units, you might think one building is larger than the other incorrectly. Similarly, maintaining consistent metrics when measuring fluid systems is vital for achieving reliable results.
Key Concepts
-
Dimensionless Numbers: Quantities like Sherwood, Reynolds, and Schmidt numbers that help characterize mass transfer phenomena.
-
Mass Transfer Coefficient: A measure of how fast a substance transfers from one phase to another.
-
Convective vs Diffsive Transport: Evolution of concentration gradients, with convection being the bulk movement due to energy input versus molecular diffusion being random movement driven by concentration gradients.
Examples & Applications
The Sherwood number at an air-water interface during an oil spill can indicate the efficacy of natural dispersion of oil.
Reynolds number helps understand water body turbulence caused by wind, influencing the mass transfer rates of pollutants.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
In water and air where flows collide, Sherwood helps mass transfer abide.
Stories
Imagine a river where oil spills and the water's churn reveals how fast it fills. Understanding NSh and NRe ensures we know well how pollutants fare.
Memory Tools
Remember 'SRS': Sherwood, Reynolds, Schmidt – the trio of mass transfer we can't omit.
Acronyms
Use 'M-C-T' to recall
Mass transport
Convection
and Transfer dynamics.
Flash Cards
Glossary
- Sherwood Number (NSh)
A dimensionless number defined as the ratio of convective mass transport to diffusive mass transport.
- Reynolds Number (NRe)
A dimensionless number indicating the ratio of inertial forces to viscous forces within a fluid.
- Schmidt Number (NSc)
A dimensionless number representing the ratio of momentum diffusivity to mass diffusivity.
- Diffusion Coefficient
A parameter that quantifies the rate of diffusion of a substance.
Reference links
Supplementary resources to enhance your learning experience.
