Mass Transfer Under Different Conditions
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Dimensionless Numbers
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today, we're going to explore how dimensionless numbers help us understand mass transfer. Let's start with the Sherwood number, which is crucial for relating convective and diffusive mass transport.

How do you calculate the Sherwood number?

Great question! The Sherwood number (NSh) can be calculated by multiplying a mass transfer coefficient by relevant dimensions like length or diffusion coefficients. It's typically expressed as NSh = kA * L/D.

And how does it relate to other dimensionless numbers?

Excellent follow-up! The Sherwood number is often compared with the Reynolds number and Schmidt number. The Reynolds number indicates flow type, while the Schmidt number characterizes diffusion rates.

So, if we know these numbers, we can predict how mass will move in fluids?

Exactly! By understanding these relationships, we can better manage environments like rivers and lakes. Now, let’s summarize: The Sherwood, Reynolds, and Schmidt numbers provide essential insights into mass transfer dynamics.
Applications of Mass Transfer in Environmental Conditions
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now, let's talk about real-world applications. For instance, when examining mass transfer in lakes, quiescent conditions allow us to see how temperature gradients affect movement.

What specific factors do we consider in these cases?

We assess how temperature differences cause density gradients, which can enhance convective flow, affecting mass transfer rates.

What about wind influence in other water bodies?

Great point! In unstratified bodies, wind-induced turbulence plays a significant role. For example, the movement of air can significantly elevate mass transfer coefficients at the sediment-water interface.

So each environment requires tailored approaches?

Absolutely! Each condition, whether lakes or oceans, necessitates unique correlations for accurate predictions. In summary, always consider the specific environmental conditions when applying mass transfer theories.
Practical Example: Oil Spills in Water
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Let's apply our knowledge to a practical scenario: an oil spill involving dense and light NAPLs. What different processes would be happening?

We could have evaporation and diffusion into water, right?

Exactly! The oil will spread, and we need to consider both evaporation into the air and dilution in the water. This shows the importance of mass transfer coefficients in contaminant fate and transport.

And how does the sediment factor in here?

Great question! The interaction with sediment adds another layer, as the oil may also diffuse into sediments. Depending on the specific parameters, we adjust our calculations accordingly.

This seems complex but very interesting!

It's indeed complex, but understanding these processes is vital for environmental management. Remember, identifying the right correlations for different conditions is key!
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
The section provides an overview of mass transfer coefficients and their related dimensionless numbers, emphasizing the relationships between convective and diffusion processes. It covers various conditions affecting mass transfer, including quiescent and turbulent flows, and discusses specific applications such as wind-induced mass transfer and the impact of temperature gradients.
Detailed
Mass Transfer Under Different Conditions
In this section, we explore the fundamentals of mass transfer and the quantitative relationships that describe it within various environmental contexts. The primary dimensionless numbers related to mass transfer include the Sherwood number (NSh), which represents the ratio of convective mass transfer to diffusive mass transport, the Reynolds number (Re) that reflects the relationship of inertial forces to viscous forces, and the Schmidt number (Sc) that relates to the diffusion of mass in fluids.
Key Elements of Mass Transfer
- Sherwood Number (NSh): This collects the convective mass transport properties into a dimensionless format, allowing for analysis across different systems such as lakes and rivers.
- Reynolds Number (Re): It gives insight into the type of flow, whether laminar or turbulent, and is calculated based on fluid velocity and viscosity, affecting the mass transfer coefficient.
- Schmidt Number (Sc): This incorporates kinematic viscosity and provides a scale for comparing mass diffusivity.
Applications in Environmental Quality
- The text elaborates on specific conditions like quiescent water bodies, where convection occurs due to temperature gradients, and correlations for mass transfer coefficients in both lakes and the sea.
- It emphasizes the necessity of understanding these parameters for effective river and lake management, especially concerning sediment and water interactions, as seen in the case of spills involving dense and light non-aqueous phase liquids (NAPLs).
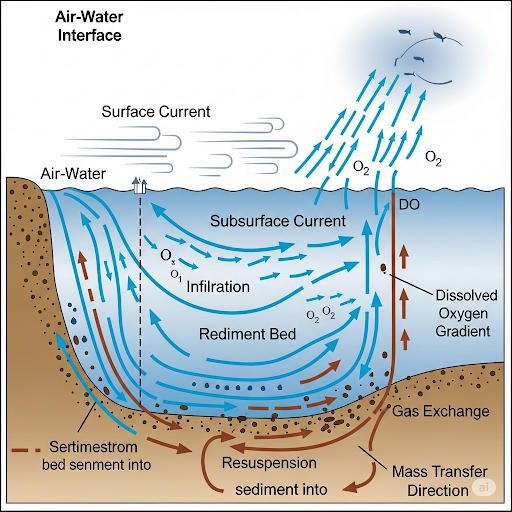
In conclusion, the section not only covers theoretical aspects but also sets the groundwork for the practical application of mass transfer principles in environmental engineering.
Youtube Videos










Audio Book
Dive deep into the subject with an immersive audiobook experience.
Understanding Key Parameters
Chapter 1 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
A good correlation is usually dimensionless, which has a lot of advantages in terms of the units that we use. For mass transfer coefficients, the nomenclature is typically in the form of Sherwood number (NSh). NSh is defined as: NSh = (kA * L) / D, where kA is the mass transfer coefficient, L is a length scale, and D is the diffusion coefficient.
Detailed Explanation
This chunk introduces the concept of dimensionless correlation in mass transfer. The Sherwood number (NSh) is a dimensionless number that provides insight into mass transfer processes. It is defined as a ratio of the convective mass transport to the diffusive mass transport. Essentially, NSh relates the rate of mass transfer (indicated by kA, the mass transfer coefficient) with the geometry of the system (given by L, the length scale) and the physical properties of the fluid (represented by D, the diffusion coefficient). This relationship helps in understanding how effectively substances transfer between phases, which is crucial in various engineering applications.
Examples & Analogies
Imagine trying to mix a spoonful of sugar into a cup of tea. If you stir slowly (low velocity, similar to low kA), the sugar dissolves slowly (similar to a high diffusion coefficient). However, if you stir quickly (high velocity, similar to high kA), the sugar dissolves quickly. The Sherwood number helps to quantify these processes by comparing the effect of stirring (convection) to how fast the sugar would naturally dissolve without any stirring (diffusion).
The Role of Reynolds Number
Chapter 2 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
The Reynolds number (Re) is defined as: Re = (Inertial Forces) / (Viscous Forces). It is affected by fluid velocity, density, and viscosity. A high Reynolds number indicates that inertial forces dominate over viscous forces.
Detailed Explanation
This chunk discusses the Reynolds number, a critical dimensionless parameter in fluid dynamics. It indicates whether the flow of fluid is laminar (smooth) or turbulent (chaotic). If the Reynolds number is high, it usually implies that the flow is turbulent, meaning that the influence of inertia is greater than viscosity. This is important in mass transfer situations because turbulent flow can enhance mixing and mass transfer as it promotes greater interaction of fluid layers compared to laminar flow, where layers slide over each other with minimal mixing.
Examples & Analogies
Think of the difference between a gentle stream (laminar flow) and a raging river (turbulent flow). In the gentle stream, the water moves smoothly, and if you drop a leaf, it gently sinks. However, in the raging river, the fast-moving water swirls and mixes, carrying leaves along rapidly. The Reynolds number helps engineers decide how to mix substances effectively in processes like chemical reactors.
Understanding Schmidt Number
Chapter 3 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
The Schmidt number (Sc) is defined as: Sc = (Viscous Forces) / (Diffusion Forces). It provides insights into the relative importance of momentum diffusion versus mass diffusion.
Detailed Explanation
The Schmidt number is another dimensionless parameter that helps characterize mass transfer in fluid systems. It compares the rate of momentum diffusion (how fast momentum spreads through the fluid) to the rate of mass diffusion (how fast substances spread). A low Schmidt number suggests that mass diffusion is quick relative to momentum diffusion, while a high Schmidt number indicates the opposite. This distinction is crucial for understanding how substances behave in various fluid flow conditions.
Examples & Analogies
Consider how food coloring disperses in water when you drop it in. If you do this in thick syrup (high viscosity), the food coloring spreads slowly compared to water (low viscosity), where it spreads rapidly. The Schmidt number helps to predict how substances like pollutants spread in rivers or lakes, impacting how we assess environmental quality.
Correlations for Mass Transfer
Chapter 4 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
In mass transfer analysis, it is essential to utilize established correlations based on experimental data. Various conditions, including quiescent and turbulent conditions, affect mass transfer coefficients significantly.
Detailed Explanation
This chunk emphasizes the importance of using empirical correlations when analyzing mass transfer processes. These correlations are derived from experimental observations and include factors such as fluid type, flow conditions (quiescent or turbulent), and environmental elements unique to the application (like wind or temperature gradients). Different environments, like lakes versus oceans, each demand tailored approaches for accurate predictions of mass transfer coefficients.
Examples & Analogies
Imagine baking a cake and using a recipe (correlation) that specifies the ingredients and conditions you'll need. Just as you can't use a chocolate cake recipe for a vanilla cake, different mass transfer situations require unique correlations grounded in experimental research to ensure accurate predictions of behavior in various environments.
Practical Implications in Environmental Studies
Chapter 5 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Mass transfer principles play a significant role in understanding environmental processes, such as the dispersion of pollutants in water bodies and the impact of chemical spills.
Detailed Explanation
This chunk connects the theoretical concepts of mass transfer to practical environmental challenges. Understanding how substances move through different phases (e.g., air, water, and sediment) is critical for assessing pollution impacts and designing remediation strategies. For instance, knowing the mass transfer coefficients in contaminated rivers can help predict how quickly a pollutant will spread, influencing clean-up strategies and policies.
Examples & Analogies
Consider a scenario where a river is contaminated with oil from a spill. Understanding mass transfer allows environmental scientists to predict how quickly and far the oil will spread, helping them decide whether to deploy booms to contain the oil or apply dispersants to break it down. Based on the iterations of mass transfer principles, they can create effective plans to mitigate the impact of spills on ecosystems.
Key Concepts
-
Dimensionless Numbers: Essential for understanding the relative strength of different phenomena in mass transfer.
-
Environmental Conditions: Mass transfer coefficients vary significantly based on the physical state and flow conditions of the environment.
Examples & Applications
Example 1: In rivers, where flow is turbulent, we will see a high Reynolds number, indicating that mass transfer is predominantly convective.
Example 2: An oil spill on a lake, where quiescence is present, will lead primarily to diffusion-driven mass transfer due to minimal water movement.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
Sherwood shows the flow's divide, Diffusion's friend and convection's guide.
Stories
Imagine a river with fish swimming fast (turbulence) and a quiet lake with ducks resting (quiescence), where the fish spread their food through speed while the ducks wait for the bread to sink (diffusion).
Memory Tools
Remember 'SRS' for mass transfer: Sherwood, Reynolds, Schmidt!
Acronyms
To remember mass transfer types
'CDT' - Convection
Diffusion
Temperature effects.
Flash Cards
Glossary
- Sherwood Number (NSh)
A dimensionless number that represents the ratio of convective mass transfer to the diffusive mass transfer.
- Reynolds Number (Re)
A dimensionless number that indicates the ratio of inertial forces to viscous forces in a fluid flow.
- Schmidt Number (Sc)
A dimensionless number that represents the ratio of momentum diffusion (kinematic viscosity) to mass diffusion.
- Kinematic Viscosity
A measure of a fluid's resistance to flow under its own weight, typically represented as the ratio of dynamic viscosity to fluid density.
- Quiescent Conditions
Situations where the fluid movement is minimal, often allowing for steady temperature or concentration gradients.
Reference links
Supplementary resources to enhance your learning experience.
