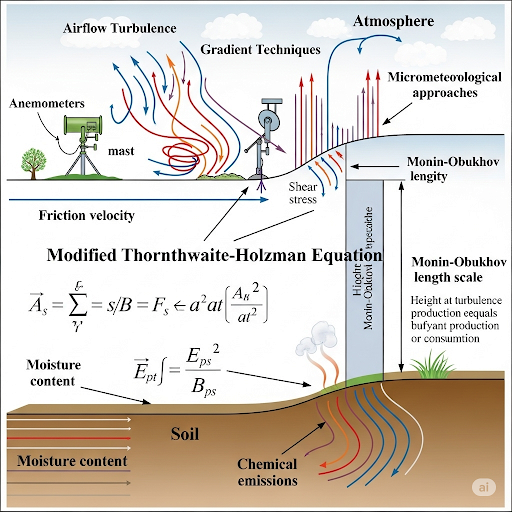
Modified Thornwaite-Holzman Equation
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introducing the Thornwaite-Holzman Equation
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today, we're discussing the Thornwaite-Holzman Equation, essential for understanding flux changes in soils affected by moisture content. Can anyone tell me what we mean by 'flux'?

I think flux refers to how much of something, like water or a gas, is moving through a given area.

Exactly! Flux essentially measures the movement of a substance. Now, in the context of soil, what factors do you think might affect this flux?

Changing moisture levels can definitely impact flux.

Correct! Changes in moisture content lead to variations in partition constants as well. How do these changes manifest practically?

They can affect how emissions are released from the soil.

Great observation! It’s essential to measure flux accurately, but sometimes direct measurements aren't possible. That’s where gradient techniques come into play.

Let’s summarize: flux is the measure of substance movement, and changes in moisture content affect the flux and partition constants.
Gradient Techniques
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now that we understand flux, let’s discuss how to measure it when direct enclosure is not feasible. Does anyone know what a gradient technique is?

Isn’t it about measuring the concentration difference over a certain distance?

Exactly right! We use the concentration difference to calculate flux, typically requiring knowledge of diffusion coefficients. Can anyone think of a scenario where this might be useful?

When we have a contaminated site and want to know how much contaminant is moving away from it?

Absolutely! That’s a perfect example. We also consider air turbulence in these calculations. Why do you think turbulence affects our measurements?

Because it can mix the air and change the concentration gradients?

Exactly! Turbulence creates convective mass transfer. Therefore, when measuring flux, we must account for both the concentration gradient and turbulence.

To recap, gradient techniques are crucial for measuring flux when direct measurement isn't possible, and we must consider turbulence in our calculations.
Friction Velocity and Stability
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Next, let’s explore friction velocity, a key component of our equation. What is friction velocity, and why is it important?

Is it related to the shear stress at the surface and the density of the air?

Yes! Friction velocity is essentially a measure of how much momentum is transferred. How does this relate to our discussions on concentration and temperature?

It shows how turbulence affects mass flux and concentration distribution.

Exactly! Turbulence can alter both momentum and mass transfer. Now, about Monin-Obukhov length scale: how do you think it figures into our discussions?

It likely relates to the stability of the atmosphere and turbulence production.

Precisely! It assesses when buoyancy exceeds shear stress and helps correct our equations for accurate flux calculations. To sum it up, friction velocity is about momentum transfer, and the Monin-Obukhov length scale helps modify our calculations based on atmospheric stability.
Final Equation and Corrections
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Finally, let's consolidate everything we’ve learned into the final expression of the modified Thornwaite-Holzman equation. Can someone recap these main components?

We have velocity gradients, concentration gradients, and now temperature gradients!

excellent! By adding temperature gradients, we address the thermal forces at play in atmospheric conditions. Why is it important to consider all these gradients?

Because they all contribute to understanding how materials move within the atmosphere.

Exactly! Accurate estimations of flux require a comprehensive understanding of these variables. What challenges can arise when using these equations?

We might not get instantaneous concentration measurements.

Right! Delays in measuring concentrations can affect our calculations. However, by applying correction factors, we refine our estimates. To recap, the modified equation integrates multiple gradients, with corrections for thermal effects.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
This section elaborates on the Modified Thornwaite-Holzman Equation and the methods to measure flux when direct measurement is challenging due to factors like moisture change and turbulence. It introduces principles such as convective mass transfer and the significance of parameters like friction velocity and Monin-Obukhov length scale.
Detailed
Detailed Summary of the Modified Thornwaite-Holzman Equation
The Modified Thornwaite-Holzman Equation is crucial in environmental science, particularly in the context of estimating fluxes in soils and the atmosphere under varying moisture conditions. This section discusses how moisture content changes affect chemical emissions and the role of partition constants in these changes.
To measure flux when direct enclosure is impractical, methods like gradient techniques and micrometeorological approaches are introduced. These techniques are based on the relationship between concentration and velocity gradients, facilitated by airflow turbulence. The section also emphasizes the importance of understanding the vertical structure of air and the mechanisms of convective mass transfer, particularly in scenarios where thermal forces are present.
The concept of friction velocity is introduced, describing its relationship with velocity gradients and surface shear stress. Additionally, the Monin-Obukhov length scale is defined as a critical parameter in understanding turbulence generation by buoyancy effects. The modified equation incorporates correction factors dependent on stability, allowing for better estimation of flux in atmospheric conditions. Ultimately, while the equation provides valuable insights, it is noted that inaccuracies may arise from concentration measurement limitations, emphasizing the need for comprehensive measurements across various heights.
Youtube Videos










Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Flux Measurement
Chapter 1 of 6
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
When you have a surface and you have to measure the flux and it is difficult for you or it is unreliable for you to enclose a surface, you need to still measure the flux and we do it by what is called as a gradient technique or a micrometeorological technique.
Detailed Explanation
This chunk discusses methods to measure flux when it's not feasible to encase the surface. Instead of enclosing it, scientists use a gradient technique, which involves examining changes in concentration of vapor or particles in the air above the surface. This technique provides an indirect way to calculate the flux by measuring differences in concentration at different heights.
Examples & Analogies
Imagine you want to measure the amount of perfume released from a bottle but can't capture it in a container. Instead, you could take measurements of how strong the scent is at various distances from the bottle. By knowing how the scent strength decreases with distance, you can estimate how much perfume is being released, similar to measuring flux using the gradient technique.
Convective Mass Transfer
Chapter 2 of 6
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
What is happening here is this turbulence that is happening and turbulence is happening in convective eddies that are this kind of structure while it is moving in this direction.
Detailed Explanation
This chunk explains the role of turbulence in the process of convection. Turbulent flow results in convective eddies, which are swirling motions in the fluid that affect how substances, like gases or liquids, are transported. Understanding turbulence is crucial because it influences how fast and effectively materials are transferred from one area to another, especially in the context of measuring flux.
Examples & Analogies
Think about stirring a pot of soup. The swirling motion creates currents that help distribute the heat and flavors throughout the soup, much like how turbulent flow helps move particles or vapor in the air above a surface. Just as the soup’s ingredients mix due to stirring, air particles mix due to turbulence, affecting the measurements we make.
Thornwaite-Holzman Equation Basics
Chapter 3 of 6
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
In turbulent processes, the idea is that velocity has a gradient, and the structure of this gradient is usually logarithmic relation where velocity in the x direction is a function of z.
Detailed Explanation
This segment introduces the Thornwaite-Holzman equation, which relates air velocity to height through a logarithmic gradient. In simpler terms, it explains that as you move up from the ground, the speed of the wind increases in a predictable way. This relationship helps scientists understand how different environmental conditions affect flux measurements.
Examples & Analogies
Imagine standing outside on a windy day. If you crouch close to the ground, you feel less wind than if you stand up tall. The height at which you are located affects how much wind you feel, similar to how air velocity changes with height according to the Thornwaite-Holzman equation.
Friction Velocity Concept
Chapter 4 of 6
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
The friction velocity is defined as shear stress at the surface divided by the density, and based on this equation, you can derive expressions that will help us understand the flux better.
Detailed Explanation
The concept of friction velocity relates the forces at the surface (shear stress) to the density of the air. This measure helps to quantify how the wind interacts with surfaces like soil or water. Understanding friction velocity is essential for applying the Thornwaite-Holzman equation to real-world scenarios, enabling better flux estimations.
Examples & Analogies
Consider how a strong wind pushes against a wall; the push causes friction. Similarly, the wind near the surface experiences friction due to the ground. Friction velocity helps us measure this force, akin to measuring how hard the wind hits the wall. This measurement allows us to predict how air and particles move in the atmosphere.
Modified Thornwaite-Holzman Equation and Stability Effects
Chapter 5 of 6
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
When you have thermal forces, you bring into this question a correction factor depending on the stability as well – which when we calculate, is based on the Monin-Obukhov length scale.
Detailed Explanation
This chunk discusses how the original Thornwaite-Holzman equation is adjusted for thermal forces affecting the air movement, introducing the Monin-Obukhov length scale. This scale measures the balance between thermal stratification and wind shear, providing crucial information for accurately calculating flux when temperature gradients play a role.
Examples & Analogies
Think of a hot air balloon. When the air inside is heated, it rises due to lower density compared to cooler air. This is similar to how thermal forces alter air movement in the atmosphere. The Monin-Obukhov length scale helps scientists understand how these temperature differences impact airflow and material flux, much like knowing how much heat is needed to lift the balloon.
Final Equation for Flux Calculation
Chapter 6 of 6
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Based on these principles, the final expression for the flux at a surface accounts for changes in velocity, concentration, and temperature gradients.
Detailed Explanation
The final equation incorporates multiple gradients, allowing for a comprehensive understanding of flux based on temperature, concentration, and velocity. This first looks complex but provides a detailed picture of how materials move from the surface to the atmosphere. It reflects the real-world interactions that affect pollution dispersion and environmental monitoring.
Examples & Analogies
Imagine baking cookies: if you change the temperature of the oven, the baking time (flux) changes based on the ingredients (concentration) and the size of the cookies (velocity). The final flux equation is like adjusting the recipe based on all these factors to get the perfect cookie, illustrating how real-world conditions change material movement.
Key Concepts
-
Flux: The rate of movement of substances through a specific area.
-
Partition Constant: Reflects how substances partition between different phases.
-
Friction Velocity: Vital for characterizing momentum transfer in turbulent flows.
-
Gradient Technique: An essential method for measuring flux when direct methods aren't viable.
-
Monin-Obukhov Length Scale: Indicates the balance between thermal and shear effects in the atmosphere.
Examples & Applications
For a contaminated site, measuring the amount of pollutant flux can help in assessing environmental impacts.
Wind tunnel studies can illustrate how different velocities influence the concentration of pollutants dispersal.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
Flux flows like a stream, through soil it will gleam, measuring emissions, is the environmental theme.
Stories
Imagine a river flowing through varied landscapes. The partition constant is like the river's banks, guiding how much water flows from one side to the other. When rain changes the landscape (moisture content), the flow adjusts, just like emissions vary in response.
Memory Tools
Friction Velocity, Monin-Obukhov — imagine a car speeding through a turbulent storm, impacted by wind and rain. Keep the acronym FVMO in mind!
Acronyms
To remember the key factors in flux measurement
- Friction velocity
- Partition constant
- Gradient technique
- Stability (Monin-Obukhov length scale) = FPGS.
Flash Cards
Glossary
- Flux
The rate of flow of a property per unit area, often seen in the context of moisture or emissions movement.
- Partition Constant
A coefficient that expresses the ratio of a substance's concentration in two different phases, like air and soil.
- Friction Velocity (v*)
The velocity scale derived from the shear stress at the surface of a fluid; used to characterize turbulent flow.
- MoninObukhov Length Scale
A length scale that balances the effects of buoyancy and shear stress, relevant in atmospheric boundary layer theory.
- Gradient Technique
A method used to estimate flux by measuring concentration gradients over a certain distance.
Reference links
Supplementary resources to enhance your learning experience.
