Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Initial Conditions and Uniform Contamination
Unlock Audio Lesson
In our model, we start by assuming that the contaminant is uniformly distributed throughout the sediment. Can anyone tell me what the initial concentration, denoted as V0, represents here?
It represents the concentration of the contaminant in pore water at the start of our analysis.
Exactly! This indicates that at t=0, every point in our sediment has the same initial concentration. Let's remember the acronym INIT for Initial conditions of uniformity. Why is it important to consider uniform contamination?
Because it simplifies our calculations and allows us to use analytical solutions more easily.
Right! Simplifications help us focus on the key aspects of the problem without getting bogged down in complexity. Let’s summarize: INIT stands for Initial uniform concentration. Next, we will explore how this concentration changes over time.
Boundary Conditions in the Model
Unlock Audio Lesson
Now, let's discuss boundary conditions. We have two key types: the semi-infinite and steady-state boundary conditions. Can anyone explain what these are?
The semi-infinite condition assumes that the initial contaminant concentration applies indefinitely away from the interface.
The steady-state condition indicates that the flux at the interface is constant over time.
Wonderful! Remember the mnemonic SSS for Steady State and Semi-infinite. Now, why do we need these conditions? What do they help represent?
They help us accurately model how contaminants move from the sediment into water, ensuring we understand the dynamics at play.
Exactly! Understanding the dynamics is crucial for effective environmental monitoring and risk assessment. Let’s summarize: SSS stands for Steady-state and Semi-infinite conditions.
Diffusion and Convection Mechanisms
Unlock Audio Lesson
Discussion often arises about the rates of diffusion and convection. What factors affect these processes in our modeling?
Concentration gradients and the mass transfer coefficients are key factors.
Also, if diffusion is slow, it controls overall transfer rates, while convection can enhance the mass transfer if it’s fast.
Great insight! The acronym DCD for Diffusion Controls Diffusion highlights how diffusion primarily governs slow transfer processes. Can you remember a practical instance where diffusion was dominant?
In cases of oil spills where contaminants diffuse slowly into water!
Right! Great example. Let’s summarize: DCD indicates that diffusion controls the transfer rate under slow conditions.
Modeling Flux with Analytical Solutions
Unlock Audio Lesson
Now, let’s look at the analytical solutions for flux. We can express flux as a function of time and concentration differences using mathematical expressions. Who can summarize the core equation from the last class?
The flux equation incorporates the initial concentration, mass transfer coefficients, and various functions like error functions.
This suggests the flux changes over time as the concentration gradients evolve!
Absolutely! The equation can be complex, but remember through the acronym FCT for Flux Changes over Time, we can analyze flux variations during contaminant transport. Why is it important to know how flux changes?
It lets us build better predictive models for environmental impact assessments.
Exactly! These models are essential for planning remediation strategies. Let’s recap: FCT signifies that Flux Changes over Time need careful analysis.
Resuspension Mechanisms and Their Effects
Unlock Audio Lesson
Finally, let’s explore resuspension. Can anyone explain how resuspension occurs in our sediment transport model?
It happens when water turbulence dislodges sediment particles, turning them into suspended solids.
And this can increase the turbidity and contaminant levels in the water, right?
Very good! The acronym TURB for Turbidity from Resuspension a Key Issue reminds us that turbidity can signal contamination risk in the water. Why do we need to be aware of this?
Because elevated turbidity can lead to decreased water quality and affect aquatic life!
Exactly! Let’s summarize: TURB indicates the risks associated with turbidity from sediment resuspension. We need to keep our eyes on these dynamics.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section examines contaminant transport within sediments, explaining initial conditions, steady-state and semi-infinite boundary conditions. It discusses analytical solutions for flux and the factors impacting diffusion and convection, as well as modeling techniques for predicting contaminant transport over time.
Detailed
Detailed Summary
In this section, we explore analytical solutions for flux in the context of contaminant transport from sediments to water. The initial focus is on the uniform distribution of contaminants in sediment, leading to the formulation of a semi-infinite system model, where initial conditions dictate the concentration of the contaminant A in pore water at z=0.
We consider both the semi-infinite boundary condition and the steady-state boundary condition applied at the sediment-water interface. The model accounts for diffusion across the interface and highlights the crucial roles of mass transfer coefficients in sediment and water, illustrating that overall transfer rates are determined by the slower of the two mechanisms.
The section further traverses the derivation of equations governing flux, where it is emphasized that flux is influenced significantly by time and the concentration gradient. With specific focus on error functions and complementary error functions, we observe the behavior and changes in flux over time and discuss the mathematical modeling of diffusion-controlled transfer.
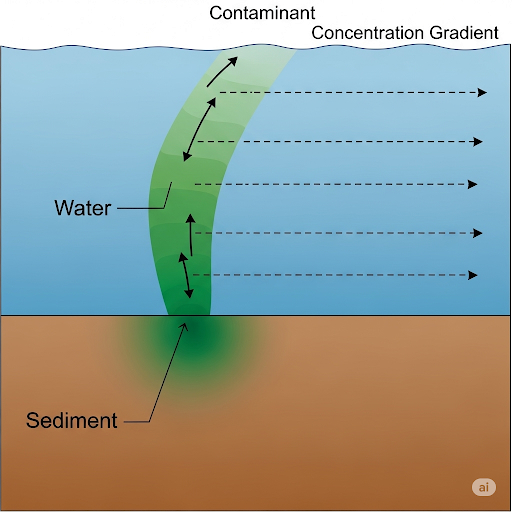
Finally, we introduce alternative boundary conditions that can simplify mathematical analysis of flux, particularly when convection effects dominate, and conclude with considerations of resuspension mechanisms affecting overall contaminant transport. The complexities involved highlight the multifaceted interactions between sedimentary processes and water quality, emphasizing the ongoing relevance of sediment management in environmental engineering.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Initial Conditions and Semi-Infinite System
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Okay, so we will continue from where we had stopped last time. We will just recap a little bit. We were talking about contaminant transport in sediments. ... it is usually not true, but for this purpose of getting an analytical solution, this is okay.
Detailed Explanation
In this chunk, we discuss the initial conditions for a model of contaminant transport in sediments. The model assumes a semi-infinite system, meaning that the sediment layer is so thick that we can ignore the boundaries below a certain depth. The concentration of contaminant, denoted as V, is uniform at the initial time (t=0) and equals V0 in the pore water, which simplifies our calculations. The setup is necessary to derive analytical solutions, even though, in reality, contaminant concentrations may not be uniform.
Examples & Analogies
Think of a sponge soaked in water. When you first drop the sponge into a container of water, the water spreads evenly throughout the sponge. Initially, every bit of the sponge has the same amount of water (uniform concentration). If you then take that sponge out and hold it over a sink, the water will start to drip out unevenly—the surface will begin to lose water first, while the inside remains saturated for longer. This illustrates the concept of initial uniformity in concentration before processes like diffusion make layers different over time.
Boundary Conditions and Flux Control
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Then we also have @ = , @ = 0 , what this means is that very far away from the surface, see the surface is where all the activities, mass transfer, main bulk of the mass transfer is happening...
Detailed Explanation
This chunk discusses boundary conditions at the edge of the sediment layer, specifically at the surface (z=0). At the surface, the concentration of the contaminant is influenced by both diffusion into the sediment and mass transfer via convection. The concentration above the surface, denoted as V∞, is considered negligible compared to the surface concentration (V0). As time progresses, concentration at the surface depletes due to the transfer of contaminant into the surrounding water. The overall flux will depend on the slower of the two processes—either diffusion from the sediment or the convection in the water, a concept commonly referred to as 'mass transfer resistance.'
Examples & Analogies
Imagine a crowded party where people are trying to leave through a narrow door. Some people (representing the contaminant) try to squeeze through (diffusion), while others have already exited and are waiting outside (convection). If the door is too narrow (slow diffusion), even if there are many people trying to get out, the flow will be limited by how fast one can pass through that door. This situation illustrates how the overall exit (or flux) is determined by the slowest process.
Analytical Expressions for Flux
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So, we had given a long big solution for this in the last class, I had given you a solution ... where this flux is given as...
Detailed Explanation
This section presents the mathematical framework for calculating the flux of contaminants from sediment into water. It mentions a specific analytical solution involving error functions and complementary error functions, which are common in diffusion problems. These functions help describe how the concentration changes over time and distance. The solution emphasizes that as time increases, the flux tends to decrease, indicating that the initial availability of the contaminant is higher right after the contamination event.
Examples & Analogies
Consider baking a cake. When you first take the cake out of the oven, it’s very hot and smells delicious (high initial 'flux' of scent). However, as time passes and the cake cools down, the smell becomes less intense (the flux decreases). Similarly, the contaminant's presence is strongest initially and then reduces over time as it moves away from the source.
Impact of Resistance Factors on Flux
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So typically we will see that the convection is much faster than the diffusion, we expect that...
Detailed Explanation
This chunk emphasizes that in most scenarios, the flow of water (convection) will be more rapid than the rate of diffusion of the contaminant. This means that the overall rate at which contaminants escape from sediments into water is primarily controlled by the diffusion rate, since it acts as the limiting factor. The discussion points towards the understanding that if diffusion is slow, it will dictate the flux regardless of how quickly water is moving past the sediment.
Examples & Analogies
Imagine trying to stir a thick soup with both a spoon and a straw. The spoon can stir quickly (like convection carrying water), but if the soup itself is very thick (like slow diffusion), the overall mixing depends on how effectively the spoon can lift and incorporate the soup. Here, disturbance in the liquid (stirring) is fast, but the actual mixing (diffusion) takes time.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Initial Concentration (V0): The starting concentration of a contaminant in pore water, crucial for modeling.
-
Semi-Infinite Boundary: A boundary condition allowing for simplification in models where one end extends infinitely.
-
Diffusion: The movement of particles from a region of higher concentration to one of lower concentration, vital in contaminant transport.
-
Steady-State Condition: A state where the properties within the system remain unchanged over time.
-
Resuspension: The process of sediment particles being lifted back into the water column, affecting water quality and contaminant levels.
-
Mass Transfer Coefficient: A key parameter in determining the rate at which contaminants transfer between phases.
-
Error Function: A mathematical function used to evaluate diffusion processes, particularly in analytical solutions.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Example 1: An oil spill contaminates sediment. Initial flux calculations use V0 to predict the rate of dispersal into the surrounding water over time.
-
Example 2: During flood events, resuspension increases turbidity in local waterways, affecting aquatic life and prompting environmental monitoring.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
In the sediment, contaminants flow, Flux tells us how fast they go.
📖 Fascinating Stories
-
Imagine a river that stirs the mud up, the particles dance and swirl in a turbulent cup, some settle down, while some float away, the resuspension game is in full play.
🧠 Other Memory Gems
-
Remember SSS for Steady State and Semi-infinite, to help recall boundary conditions neat.
🎯 Super Acronyms
Use TURB to remember that Turbidity from Resuspension is a Key Issue in water quality.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Flux
Definition:
The rate at which a substance flows through a surface, often quantified in mass per unit area per time.
-
Term: SemiInfinite System
Definition:
A modeling approach where one end of the system is considered to extend infinitely, allowing for simplifications in boundary conditions.
-
Term: Diffusion
Definition:
The process by which particles spread from areas of high concentration to areas of low concentration.
-
Term: Convection
Definition:
The movement of fluid that results from the combined effects of diffusion and bulk motion.
-
Term: Error Function
Definition:
A mathematical function that describes the probability of a variable falling within a specified range in a normal distribution.
-
Term: Resuspension
Definition:
The process of dislodging sediment particles from the sediment-water interface, which can increase turbidity in water.
-
Term: Mass Transfer Coefficient
Definition:
A proportionality constant that relates the mass transfer between phases to the concentration difference.
-
Term: SteadyState Condition
Definition:
A condition where system variables remain constant over time, leading to a predictable and stable state.
-
Term: Turbidity
Definition:
An optical property of water that reflects the presence of suspended solids, affecting water clarity.
Reference links
- Understanding Boundary Conditions in Diffusion Problems
- Diffusion Coefficients and Environmental Transport
- Marine Sediment: The Role in Water Quality
- Turbidity and Water Quality in Lakes
- Resuspension in Aquatic Systems and Its Environmental Impacts
- Introduction to Mass Transfer Coefficients
- Error Functions in Engineering and Science