Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Contaminant Diffusion
Unlock Audio Lesson
Today, we'll begin by discussing how contaminants move within sediments. Can anyone tell me what diffusion is?
Isn't it the process where substances move from areas of high concentration to areas of low concentration?
Exactly! So, in our context of sediments, contaminants will disperse due to concentration gradients. This process is essential for understanding how pollutants affect water quality.
How does this diffusion work in the sediment-water interface?
Great question! At the sediment surface, we have a driving force that allows contaminants to diffuse into the water, typically governed by the concentration gradient. We can recall the acronym DAMP for remembering the main factors: Diffusion rate, Area, Mass, and Pressure differ.
What happens to the concentration over time?
As time progresses, the surface concentration decreases due to the material being transported into the water where it can dilute further.
So does that mean the concentration in the sediment will eventually become zero?
Not exactly zero, but it will decrease significantly over time. We'll analyze this further as we continue!
To summarize, diffusion is a key mechanism for contaminant transport, heavily impacted by concentration gradients. Remember that DAMP acronym!
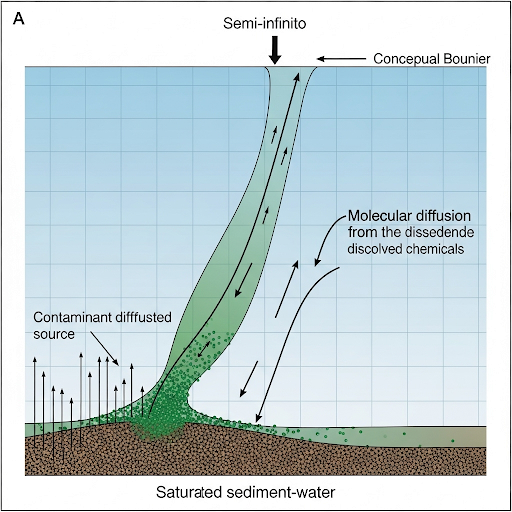
Semi-Infinite Systems and Boundary Conditions
Unlock Audio Lesson
Let’s talk about semi-infinite systems. Why do we consider sediment depth as semi-infinite?
Is it because the concentration remains constant far from the surface?
Exactly! This allows us to simplify our equations because we assume at far depths, concentration does not change due to initial contamination.
What boundary conditions should we keep in mind then?
Good point! The top boundary condition indicates that the material diffuses to the water interface, while at depth, we assume a constant concentration. Both are essential for operational calculations for contaminant flux.
What mathematical tools can help analyze these conditions?
We often use error functions in our calculations! The functions model how concentration changes over time effectively. For a quick memory, remember EXP for 'Error Functions in a Process.'
So, we can derive flux rates using these functions?
Yes! The flux rate can drop over time depending on diffusion rates, calculated through these functions and initial conditions.
In summary, boundary conditions are integral to understand contaminant transport in semi-infinite systems, and error functions play a vital role in our calculations.
Contaminant Resuspension and Its Impacts
Unlock Audio Lesson
We’ve talked about diffusion; now let's explore a different mechanism: resuspension. What do you think resuspension involves?
Is it when sediment particles are lifted back into the water column due to turbulence?
Exactly! Turbulence from water flow can dislodge sediments, mixing contaminants into the water. It’s essential for understanding water quality during events like flooding.
Could you give an example of how this affects water quality?
Sure! During heavy rainfall, sediments can carry heavy contamination downstream. The acronym CLEAN can represent this: Contamination Load at Environmental Assessment of New being—meaning hydrology can significantly affect assessments.
What implications do these particles have after being resuspended?
Great question! Once in the water, they can not only remain suspended for long periods, but some may also get into the food chain.
So, the concern is not just immediate pollution but further ecological impacts?
Exactly! Resuspension can lead to long-term ecological changes, making it critical to consider in risk assessments.
In summary, resuspension intertwines with sediment transport and can lead to significant water quality issues, affecting ecosystems and human health.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In this section, we explore how contaminants are transported within sediments through diffusion and mass transfer, specifically analyzing the conditions that affect transport rates, such as the concentration gradients and the resistance of sediment and water. This foundational understanding is crucial for environmental monitoring and risk assessment.
Detailed
Contaminant transport in sediments is a significant concept within environmental science that addresses how chemical substances move from sediment to surrounding water, primarily driven by diffusion and diffusion-controlled mass transfer mechanisms. Initially, the section examines the foundational concept of uniform contaminant distribution and utilizes a semi-infinite system model to illustrate how concentration changes occur over time as a function of sediment depth and distance from the surface. Key equations and boundary conditions are introduced to characterize the system, emphasizing the role of diffusion and convective mass transfer coefficients. The section further discusses the steady-state boundary conditions and introduces the concepts of error functions and complementary error functions, providing insight into how these mathematical functions and parameters are employed in practical applications such as software modeling. Through understanding these principles, the section lays the groundwork for exploring additional contaminant transport mechanisms like resuspension, which can complicate risk assessment and environmental management.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Initial Contaminant Distribution
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Our model here is the pore water and this is w in the sediment. So, is an initial condition, what this means is that, initial contamination in the sediment is uniform, it is usually not true, but for this purpose of getting an analytical solution, this is okay.
Detailed Explanation
In this chunk, we are discussing how contaminants are initially distributed in sediments. The text mentions that the model assumes a uniform initial contamination level throughout the sediment. Though this is not a common scenario in reality, it simplifies calculations for analytical solutions. This uniformity means that at the start, the concentration of the contaminant is the same at all points in the sediment.
Examples & Analogies
Think of spreading a drop of food coloring evenly in a glass of clear water. Initially, the color spreads uniformly throughout. However, if you let it sit, the color may settle or create gradients, similar to how contaminants might behave in sediment over time.
Boundary Conditions and Their Importance
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The other boundary condition that we talked about is at z = 0, we said we have \(K_{w} \cdot (C_{A} - C_{A_{\infty}}) = -A \cdot \frac{dC}{dz} \mid_{z=0}\) where \(C_{A_{\infty}}\) is the background concentration. This is the steady state boundary condition at the surface.
Detailed Explanation
Here, the text describes boundary conditions, which are essential for understanding how contaminants move from sediment to pore water. The equation represents a situation where the concentration gradient at the surface \(z=0\) drives the movement of contaminants. \(C_{A}\) is the contaminant's concentration, while \(C_{A_{\infty}}\) is the concentration far from the surface. This relationship helps us understand how quickly contaminants can migrate under different conditions.
Examples & Analogies
Imagine a sponge soaked in water. The top surface of the sponge will have more water (higher concentration) compared to the interior (lower concentration). When you press the sponge, the water moves toward the surface, similar to how contaminants move due to concentration differences.
Diffusion vs. Convection
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Typically, we will see that the convection is much faster than the diffusion. In most cases, irrespective of what the system is, it is diffusion controlled. The rate at which material is going out is controlled by the rate at which diffusion is happening in the system, okay.
Detailed Explanation
This chunk emphasizes the difference between diffusion and convection in contaminant transport. While convection can be fast, in many sediment systems, the movement of contaminants is limited by diffusion, which is a slower process. Understanding these dynamics helps anticipate how contaminants will behave over time, as they may move through water more quickly than through sediment.
Examples & Analogies
Imagine trying to smell a perfume in a room. If someone sprays it on one side, the initial smell close to the spray is strong (convection). However, as the scent spreads through the room, it takes time to diffuse to the far corners, illustrating how diffusion controls the spread of contaminants in sediments.
Decreasing Flux Over Time
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So, as time increases, what we expect to see is the flux of contaminants as a function of time decreases, which means the value is \(K_{w} \cdot C_{A_{0}}\). This means that at time \(t=0\), there is already chemical available at the surface.
Detailed Explanation
This chunk discusses how the flux, or the amount of contaminant moving, decreases over time. Initially, there is a high concentration of contaminants at the surface, which allows for quicker movement into the water. However, as time progresses, the concentration at the surface drops and the amount that can move into the water declines.
Examples & Analogies
Consider a sponge that has been soaked in colored water. Initially, if you press it, a lot of color leaks out quickly (high flux). Over time, as the sponge loses color, it becomes harder for more color to come out, and the amount of color released decreases (lower flux).
Analysis of Contaminant Transport
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
In the general case, what we will do is that here we will put \(K_{w} \cdot (C_{A} - C_{A_{\infty}})\) where the highest flux is this value, \(K_{w} \cdot (C_{A} - C_{A_{\infty}})\). It is decreasing after that.
Detailed Explanation
This chunk elaborates on how we analyze contaminant transport over time, specifically focusing on the highest flux achievable. It re-emphasizes the significance of the initial contaminant concentration and how the declining concentration impacts the movement of the contaminants over time. Mathematically, it informs us that the assessments must consider both the concentration and the rate of change to estimate transport effectively.
Examples & Analogies
If you think of a water fountain where water is sprayed out quickly at first, it gradually slows down as the water level drops. Your rate of flow at any moment is affected by what is left in the fountain. Similarly, contaminant transport will slow as available contaminant becomes depleted.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Contaminant Transport: The movement of hazardous substances from sediments to aquatic environments.
-
Diffusion: A key mechanism for contaminant transport driven by concentration gradients.
-
Semi-infinite System: A model setup that simplifies the analysis of sediment interactions.
-
Boundary Conditions: Conditions that dictate how contaminant concentration behaves at the sediment-water interface.
-
Resuspension: The process by which sediment particles become suspended in the water column, impacting contaminant transport and water quality.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
In a lake with contaminated sediment, the diffusion of contaminants into the water column can lead to elevated pollutant concentrations that affect aquatic life.
-
Following a heavy rainfall, resuspension of sediments can occur, causing increased turbidity and potential chemical exposure in downstream waters.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
In the sediment deep where the water flows, contaminants move where the concentration goes!
📖 Fascinating Stories
-
Once in a muddy river, contaminants lay at rest until a big storm came and stirred up the best. The clouds of pollution swirled in a dance, showing that resuspension could change the chance!
🧠 Other Memory Gems
-
To remember the steps of diffusion: DAMP: Diffusion, Area, Mass, Pressure!
🎯 Super Acronyms
CLEAN
- Contamination Load at Environmental Assessment of New—helping recall how hydrology influences assessments.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Diffusion
Definition:
The process by which molecules spread from areas of higher concentration to areas of lower concentration.
-
Term: Semiinfinite system
Definition:
A modeling approach where one boundary is assumed to be infinitely far away, allowing constant conditions at that boundary for analytical solutions.
-
Term: Boundary Condition
Definition:
Conditions at the boundaries of a system that must be satisfied for a mathematical model to be valid.
-
Term: Error Function
Definition:
A complex mathematical function arising in the solutions of diffusion problems, commonly used for analyzing concentration profiles.
-
Term: Resuspension
Definition:
The process of sediment particles being lifted back into the water column, often due to turbulence.
-
Term: Mass Transfer Coefficient
Definition:
A coefficient that quantifies the rate of mass transfer in or out of a phase.