Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Iceberg Stability
Unlock Audio Lesson
Today we're going to talk about how icebergs behave in water and why only a portion is visible at the surface. Can anyone tell me what we see when we look at an iceberg?
We see the top part, which is usually much smaller than the underwater part.
Exactly! Only about one-eighth of an iceberg's volume is visible. The rest is submerged. Now, why do you think this matters?
Because the submerged part affects its stability?
That's right. If underwater melting occurs, it can change the center of buoyancy, which can be dangerous. Let’s correlate this to metacentric height, what do you know about that?
Metacentric Height and Stability
Unlock Audio Lesson
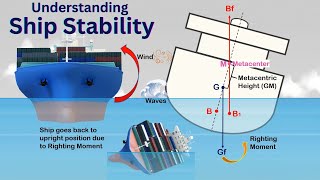
Now let’s talk about metacentric height. It’s essential for understanding stability. Can anyone explain what metacentric height means?
Is it the distance from the center of gravity to the metacenter?
Great! The metacenter is the point where the buoyant force acts when the body tilts. Why is having a higher metacentric height good for stability?
A higher metacentric height means better stability and less chance of capsizing.
Excellent! And remember, stability determines how safely our vessel will navigate. Now, let’s link this to the Titanic.
Historical Context of Icebergs
Unlock Audio Lesson
The Titanic tragedy offers a clear lesson about the importance of understanding icebergs. What happened in 1912 regarding iceberg awareness?
The ship hit an iceberg because they underestimated its size and dangers.
Correct! At that time, technologies like GPS and radar were not available. How do you think modern technology helps today?
We can detect icebergs before we reach them!
Right! The advancements allow us to visualize risks better. Let's summarize how this technology changes our understanding of fluid dynamics.
Practical Experimentation
Unlock Audio Lesson
Now, suppose we set up an experiment to measure the metacentric height of various objects. What do you think we need to do?
We can use different weights to see how it affects stability.
Exactly! We’ll balance weights on our floating model to observe changes in height. Can someone explain how this connects to real-life engineering?
It helps engineers design safer ships and buildings based on stability!
Perfect! Remember, the insights gained from such experiments can directly inform engineering practices for safety.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In this section, the relationship between the specific gravity of ice and seawater is examined to illustrate the visibility concerns regarding icebergs. It highlights how underwater melting can shift an iceberg's center of buoyancy, potentially leading to instability and collapse. The importance of metacentric height in assessing the stability of floating objects, such as ships, is also emphasized, linking it to historical events like the Titanic disaster and advocating for safety in engineering designs.
Detailed
Detailed Summary
In the context of fluid mechanics, metacentric height is a pivotal concept that pertains to the stability of floating objects. This section opens with an exploration of the dynamics of icebergs, particularly during their melting phases due to oceanic heating. It underlines a crucial observation: while only the tip of an iceberg is visible (approximately one-eighth of its total volume), the remainder, submerged, significantly affects its overall stability and buoyancy.
The consequences of underwater melting are discussed, illustrating how it can alter the center of buoyancy (CB) and lead to unexpected collapses—highlighted by historical events such as the sinking of the Titanic, which suffered due to a lack of awareness about iceberg dynamics. The authors stress the need for engineers to prioritize safety in ship design, focusing not only on aesthetics but also on understanding the principles of fluid mechanics to maintain buoyancy stability.
Further, the discussion on metacentric height introduces practical experiments that can be conducted in fluid mechanics labs to observe and measure this height and hence, assess stability. The implications for engineering practices, particularly in constructing high-rise buildings and ships, are also addressed to ensure that safety considerations take precedence over design ambition. Overall, this section connects theoretical fluid dynamics with real-world applications and safety practices, especially in navigation and engineering.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Metacentric Height
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Let us look at simple experiment, metacentric height experimental setups with just balancing the weight we can measure the metacentric height of a floating object like this and this type of facilities are there any fluid mechanics lab, you can just measure the metacentric height and find out the stability of floating object.
Detailed Explanation
In this section, we introduce the concept of metacentric height, which is essential in understanding the stability of floating objects. We can measure the metacentric height through an experimental setup. In a fluid mechanics lab, there are specific facilities designed to determine this height based on balancing weights. The metacentric height helps us evaluate whether a floating object, such as a ship or a buoy, will remain stable or capsized when disturbed.
Examples & Analogies
Imagine a seesaw where the balance point determines whether one side tips over or remains stable. Similarly, in the case of boats, if their metacentric height is sufficiently high, they will remain upright and stable in the water, even when waves or external forces act on them.
Understanding Stability of Floating Objects
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
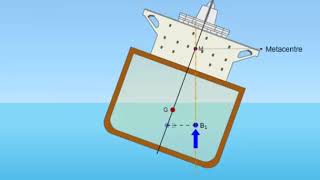
As this melting it you see that at certain points it will come it. Its center of buoyancy will change it and the point of MG what we have discussing is that, that becomes a negative and it can immediately collapsed it. So that what this very there is sudden collapse of a big iceberg is happens it which because of the presence of the underwater melting of the system.
Detailed Explanation
This chunk discusses the importance of metacentric height in relation to the buoyancy of floating objects, particularly icebergs. When an iceberg melts underwater due to rising ocean temperatures, its center of buoyancy shifts. This shift can destabilize the iceberg, leading to sudden collapses. Hence, understanding the relationship between metacentric height and buoyancy is crucial for predicting the stability of larger floating objects.
Examples & Analogies
Think of an iceberg like a large block of ice that someone's been slowly melting from the bottom. As it melts, it becomes top-heavy and may tip over unexpectedly, which is similar to how icebergs can suddenly collapse due to melting and changes in buoyancy.
Historical Context: Titanic Example
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So that is the reasons if you know it if you can see the great movie of Titanic, which is stuck in because of stuck with the iceberg in 1912 because of not under estimating, not knowing having the knowledge of the iceberg.
Detailed Explanation
This chunk highlights the historical significance of understanding iceberg behaviors, referencing the Titanic disaster in 1912. At that time, there was limited knowledge regarding the size and shape of icebergs. The Titanic’s crew underestimated the threat posed by icebergs, which was a direct result of the lack of technology and understanding of icebergs’ underwater profiles. This emphasizes the importance of studying metacentric height and buoyancy to prevent such disasters.
Examples & Analogies
The Titanic tragedy serves as a cautionary tale similar to advanced warning systems for tornadoes. Just as meteorologists now use technology to predict severe weather and prevent disasters, sailors today use improved knowledge of buoyancy and metacentric height to avoid hazards like icebergs.
Modern Navigational Technologies
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
1912 you can know it there was not much technology to do at present what we have like the space technology, the GPS technology, the radar technology, we can do details sounding what type of the iceberg is there. What is the extent of the icebergs.
Detailed Explanation
In this section, we discuss how modern technologies such as GPS, radar, and sonar have transformed our ability to navigate safely in icy waters. These developments allow us to detect the size and extent of icebergs accurately, which is crucial in ensuring safe navigation and preventing accidents like the Titanic's.
Examples & Analogies
Modern navigational tools are like having a high-tech map on your phone that alerts you about road conditions and obstacles ahead. Similarly, radar and GPS allow ships to 'see' and understand the environment surrounding them, avoiding dangers just like a driver can avoid potholes with a GPS alert.
The Importance of Safety in Engineering
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So what my point is to say that so, as a engineer who may built a big interior design, expensive ship but also you should look it the safety of the ship.
Detailed Explanation
This chunk emphasizes that engineers must prioritize safety alongside aesthetics and luxury when designing ships. It suggests that while creating visually appealing interiors is important, ensuring a ship's stability and safety is paramount. Engineers need to have a strong grasp of principles like buoyancy and metacentric height to build safe vessels.
Examples & Analogies
Consider building a luxury car. While the leather seats and high-tech features are appealing, safety features like airbags and stability control are what truly keep passengers safe in an accident. Engineers should take a similar approach when designing ships, always balancing beauty with safety.
Experimental Measurement of Metacentric Height
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now let us come it to the another component on fluid statics that means fluid at the rest. But we are looking it a rigid body motions. That means what it happens that if I have a half filled liquid containers.
Detailed Explanation
This chunk introduces a practical experiment designed to measure the metacentric height of an object. It sets the stage for understanding how liquids behave in moving containers and how we can extrapolate this understanding to analyze and predict the behavior of floating objects in fluid mechanics.
Examples & Analogies
Picture a child playing with a water bottle filled halfway with water. When the child moves quickly, the water sloshes back and forth, but comes to rest at a new level. This is similar to how we analyze the change in water level and behavior of fluids in stationary and moving containers, allowing us to measure stability factors like metacentric height.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Iceberg Visibility: Only one-eighth of an iceberg is visible above water, affecting safety and navigation.
-
Underwater Melting: Melting beneath the surface alters the center of buoyancy, which can lead to instability.
-
Metacentric Height: A higher metacentric height indicates greater stability for floating objects.
-
Buoyant Force: The upward force acting on submerged objects, crucial to understanding stability.
-
Safety in Design: The importance of prioritizing safety features in ship and building design over aesthetics.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
The Titanic disaster highlights the consequences of underestimating iceberg dynamics.
-
Experiments in fluid mechanics labs help students understand how metacentric height affects stability.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
To not hit a berg, check below, for the danger hides under the flow.
📖 Fascinating Stories
-
Imagine a ship sailing proudly, with a grand interior. But underneath, shifts in buoyancy silently threaten its fate, like an iceberg lurking below.
🧠 Other Memory Gems
-
Remember the acronym B.M.S.S.: Buoyancy, Metacentric, Stability, Safety - the essentials in designing floating objects.
🎯 Super Acronyms
MBS for Metacentric, Buoyant Force, Stability – a quick reminder for what engineers must prioritize.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Metacentric Height
Definition:
The distance between the center of gravity and the metacenter, indicating the stability of a floating object.
-
Term: Center of Buoyancy
Definition:
The centroid of the volume of fluid displaced by a floating object.
-
Term: Specific Gravity
Definition:
The ratio of the density of a substance to the density of a reference substance, usually water.
-
Term: Stability
Definition:
The ability of a floating object to return to an upright position after being tilted.
-
Term: Buoyant Force
Definition:
The upward force exerted by a fluid, counteracting the weight of an immersed object.