Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Center of Buoyancy
Unlock Audio Lesson
Today, we will begin with the concept of the center of buoyancy. Can anyone explain what it means?
Isn't it the point where the fluid force acts on an object submerged in a fluid?
Exactly! The center of buoyancy is critical in understanding stability. For example, when an iceberg melts underwater, how does that affect its center of buoyancy?
The center of buoyancy could shift, potentially leading to instability.
Correct! And if it becomes unstable, the iceberg could collapse. This is why understanding the dynamics beneath the surface is essential. Remember the mnemonic 'B.U.O.Y. - Balance Under Obvious Yonder' to think about how balancing forces keeps an object afloat.
Could you give an example of when this happened?
Sure! This principle is significant when considering events like the Titanic disaster, where the underestimation of iceberg structures led to tragedy.
So, understanding these concepts can prevent similar accidents in the future!
Absolutely! Let me summarize: The center of buoyancy significantly influences the stability of floating objects, especially when conditions change.
Metacentric Height
Unlock Audio Lesson
Next, let's talk about metacentric height. What do we know about it?
I think it’s the distance between the center of gravity and the metacenter?
Correct! If the metacenter is above the center of gravity, the object is stable. Can anyone explain why this is crucial for engineers?
Because we need to ensure that floating structures like ships can withstand forces without capsizing.
Exactly! Let's also introduce a helpful acronym: 'S.S.M.' - Stable Ships Matter. This reminds us to prioritize stability in design.
How do we measure metacentric height in a lab?
Good question! We use experimental setups to find it by balancing weights to determine stability. It's a valuable hands-on learning experience.
So, understanding metacentric height can help prevent disasters like those caused by capsizing.
Yes, that's the key takeaway! Always remember: stability is paramount in fluid dynamics.
Pressure Behavior Under Acceleration
Unlock Audio Lesson
Now, let’s examine how liquids behave under acceleration. What happens to the liquid in a half-filled container when it accelerates?
The surface of the liquid tilts!
Exactly! The tilting surface is a result of pressure changes. Does anyone remember how we can predict the angle of tilt?
Is it related to the force components involved, like gravity and acceleration?
That's right! The angle of tilt can be determined using trigonometric relationships. Let's use the mnemonic 'Tilt = T.G.A.' - Tilt is given by Gravity and Acceleration. Can anyone think of a real-life application?
In vehicles, liquid tanks shift when cornering or accelerating!
Exactly! This understanding is crucial in designing secure liquid containers in various applications. Always think about how acceleration impacts fluid dynamics!
Uniform Rotation and its Effects
Unlock Audio Lesson
Now, let's discuss uniform rotation. When a liquid is in a rotating cylinder, what happens to the free surface?
It takes on a parabolic shape!
Correct! The pressure gradient leads to this shape. Let’s remember: 'P.A.R.' - Parabolic Appearance in Rotation. What forces are at play here?
Centrifugal and gravitational forces are involved!
Exactly! Understanding this helps us in various applications, from mixers to rockets. Can anyone tell me why this understanding is essential?
It helps in ensuring that the liquid remains contained without spilling!
That’s right! Always remember, understanding these concepts is crucial for safety in engineering designs.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In this section, we examine how pressure fields behave in rotating fluids, including the concept of metacentric height and the effects of acceleration on pressure distribution. The relationship between the shape of free surfaces and pressure gradients in different contexts is emphasized, alongside real-world applications and lessons from history, such as the Titanic disaster.
Detailed
Pressure Fields in Rotating Fluids: Detailed Summary
Introduction
This section discusses the behavior of pressure fields in rotating fluids, focusing primarily on the effects of rotation and acceleration on fluid dynamics and stability.
Key Concepts
- Center of Buoyancy and Stability: The center of buoyancy shifts as an iceberg melts from below, affecting its stability and potentially leading to a sudden collapse.
- Metacentric Height: A critical property that determines the stability of floating objects. When the metacenter is above the center of gravity (CG), the object is stable. If below, it may capsize.
- Pressure Behavior Under Acceleration: When a container with liquid is accelerated, the pressure within the liquid changes. For instance, in a half-filled container, the free surface tilts, with pressure gradients adjusting according to the forces acting on the fluid (gravity and acceleration).
- Uniform Rotation and Centrifugal Effects: Understanding how rotating liquids behave—specifically that the pressure distribution within a rotating fluid leads to parabolic shapes of free surfaces due to the balance of gravitational and centrifugal forces.
Historical Context
The section touches on historical lessons such as the Titanic disaster, illustrating the consequences of poor understanding of buoyancy and fluid dynamics in engineering practices.
Conclusion
Overall, mastering the concepts of buoyancy, metacentric height, and pressure distributions in rotating fluids is essential for engineers working in fields such as marine design and fluid mechanics.
Youtube Videos
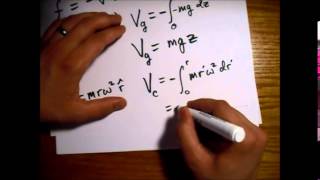
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Understanding Pressure in Accelerating Containers
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
If I have a half filled liquid container, and I accelerate it with acceleration a, we can imagine that fluid will slosh up and down. After a certain time, a new free surface will be created and sloshing will stop, acting like a rigid body moving with acceleration a.
Detailed Explanation
When a half-filled container of liquid accelerates, the liquid initially moves up and down due to inertia (slosh). However, after a while, a new, stable free surface forms. This happens because the forces acting on the liquid (gravity and acceleration) reach an equilibrium. Essentially, the liquid behaves as if it were a solid object, as there are no relative movements within it.
Examples & Analogies
Imagine riding in a car going fast around a corner. At first, you might feel the push to the side as the car turns. But once you stabilize your position—leaning against the seat—you stop feeling that push. The liquid in the container behaves similarly, adjusting until it reaches a still, stable form.
Pressure and Free Surface Relationship
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
As the accelerating container creates a new free surface, the pressure changes accordingly. The pressure gradient is influenced by the difference between gravitational acceleration and the container's acceleration.
Detailed Explanation
In the context of fluid mechanics, when the free surface of the liquid tilts due to acceleration, the pressure gradient within the fluid changes. The pressure is greatest at the bottom and reduces toward the free surface. The relationship illustrates how pressure varies with depth, taking into account both gravitational force and any external accelerative forces.
Examples & Analogies
Think of a water slide. When you start at the top and slide down, the water at the very bottom experiences more pressure from the water above. If you were to slide down while the entire slide tilts at an angle, the water would push differently depending on the angle of the slide, similar to how pressure alters based on external forces.
Rotating Fluids and Centrifugal Forces
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
When a liquid rotates uniformly in a container, centrifugal forces come into play. These forces lead to a characteristic shape of the liquid surface that is dependent on the rate of rotation.
Detailed Explanation
In a rotating fluid system, centrifugal force pushes the fluid outward, causing the fluid to take a parabolic shape. This occurs because as the liquid spins, the pressure increases with the radial distance from the center. The establishment of hydrostatic equilibrium results in a stable surface shape influenced by the rate of rotation.
Examples & Analogies
If you consider a merry-go-round, as it spins, you feel pushed outward against the seat. Water in a spinning bucket behaves similarly; the water rises higher at the sides than at the center due to centrifugal forces, forming a parabolic surface.
Analyzing Pressure Distributions
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The change in pressure due to centrifugal effects can be expressed mathematically, leading to equations that describe pressure gradients in rotating fluids. These pressure distributions help in understanding various applications in engineering.
Detailed Explanation
By analyzing pressure distributions in rotating fluids using derived equations, engineers can predict how fluids behave in practical scenarios. Understanding these gradients allows for the design of spaces and systems (like containers or tanks) that can withstand different pressures effectively, crucial for safety and functionality.
Examples & Analogies
Consider designing a roundabout in a city. Just as understanding how vehicles speed and veer off at different points can help in designing safer entries and exits, understanding how pressure changes in systems like fluid tanks can guide engineers in creating materials that won’t burst under pressure.
Practical Applications and Experimental Setups
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Practical experiments using forced vortex setups allow for the observation of fluid behavior under rotation and comparison of theoretical outcomes with actual measurements.
Detailed Explanation
Experimental setups, such as forced vortex experiments, provide insights into how fluids behave under various conditions of rotation and pressure. Engineers create experiments to validate theories and ensure their designs are safe and effective under real-world conditions.
Examples & Analogies
Think of an ice cream machine that churns to mix flavors. The way the machine rotates causes the ingredients to mix consistently, similar to how experiments model fluid behavior under rotation. Engineers use this understanding to create systems that are reliable, like water treatment facilities or rocket fuel systems.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Center of Buoyancy and Stability: The center of buoyancy shifts as an iceberg melts from below, affecting its stability and potentially leading to a sudden collapse.
-
Metacentric Height: A critical property that determines the stability of floating objects. When the metacenter is above the center of gravity (CG), the object is stable. If below, it may capsize.
-
Pressure Behavior Under Acceleration: When a container with liquid is accelerated, the pressure within the liquid changes. For instance, in a half-filled container, the free surface tilts, with pressure gradients adjusting according to the forces acting on the fluid (gravity and acceleration).
-
Uniform Rotation and Centrifugal Effects: Understanding how rotating liquids behave—specifically that the pressure distribution within a rotating fluid leads to parabolic shapes of free surfaces due to the balance of gravitational and centrifugal forces.
-
Historical Context
-
The section touches on historical lessons such as the Titanic disaster, illustrating the consequences of poor understanding of buoyancy and fluid dynamics in engineering practices.
-
Conclusion
-
Overall, mastering the concepts of buoyancy, metacentric height, and pressure distributions in rotating fluids is essential for engineers working in fields such as marine design and fluid mechanics.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
An iceberg melting underwater changes its center of buoyancy, potentially causing it to collapse suddenly.
-
In a moving vehicle, liquid in a tank can shift, creating pressure variances that might lead to spillage if not contained properly.
-
When a cylinder rotates uniformly, the free surface of the liquid takes a parabolic shape due to centrifugal forces.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
When icebergs melt, beware their shift, Center of buoyancy can cause a rift.
📖 Fascinating Stories
-
Imagine an iceberg, tall and grand, but as it melts from below, it becomes unstable, altering the ocean it stands in.
🧠 Other Memory Gems
-
To remember Metacentric Height: 'M.E.S.H.' - Metacentric Equals Stability Height.
🎯 Super Acronyms
B.U.O.Y. - Balance Under Obvious Yonder helps to recall the principles of buoyancy.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Center of Buoyancy
Definition:
The point in a submerged or floating object where the buoyant force acts.
-
Term: Metacentric Height
Definition:
The distance between the metacenter and the center of gravity of a floating object, indicating its stability.
-
Term: Pressure Gradient
Definition:
The rate of change of pressure in a fluid with respect to distance.
-
Term: Centrifugal Force
Definition:
The apparent force that acts outward on a mass moving in a circular path.
-
Term: Buoyancy
Definition:
The upward force that a fluid exerts on an object placed in it.