Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Metacentric Height
Unlock Audio Lesson
Today, we are going to discuss metacentric height. Can anyone explain what metacentric height is?
Isn't it the distance between the center of buoyancy and the metacenter?
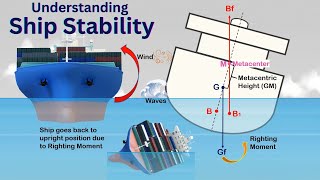
Exactly! Metacentric height helps us understand how stable a floating object will be. The greater the metacentric height, the more stable the object is. Now, why do you think this is important for ships and icebergs?
Maybe because they need to stay upright in the water without capsizing?
Right! And if we look at icebergs, only 1/8 of them is above water. The rest is submerged, and that can cause instability if it melts underneath.
Historical Lessons from Maritime Disasters
Unlock Audio Lesson
Now, let’s talk about the Titanic. What happened during its voyage that relates to our discussion on icebergs?
It hit an iceberg, and a lot of people died because they didn't see it in time!
Correct! The structure of the iceberg was underestimated. This is a classic example of not being aware of what lies beneath the surface.
So, if engineers design ships, they need to consider the potential presence of large submerged ice as a safety measure?
Precisely! This ties back to the need for integrating technology in navigation like GPS and radar systems.
Fluid Mechanics and Stability
Unlock Audio Lesson
Let’s transition to fluid mechanics. How does the behavior of liquids under acceleration relate to the stability of floating objects?
If a liquid is sloshing around in a container, it must affect the center of buoyancy?
That's correct! As the liquid stabilizes, it creates a new free surface. This also means we can consider our fluid as behaving like a rigid body when it reaches stability.
So, if the container moves with constant acceleration, how does that affect pressure?
Great question! The pressure distribution will adjust according to the forces acting on the liquid, which includes gravity and any acceleration.
Practical Experiment on Metacentric Height
Unlock Audio Lesson
Finally, let's discuss how we can practically measure metacentric height. What would we need to do?
I think we would have to balance weights on a floating object to determine how stable it is.
Exactly! By balancing weights and observing shifts in stability, we can get accurate measurements of metacentric height.
And we can use this data to improve ship designs, right?
Correct! Engineers can apply this knowledge to enhance the safety and design of vessels.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section emphasizes the importance of understanding metacentric height to ensure the stability of floating structures. It explores how factors such as underwater melting of icebergs can impact their buoyancy and stability. Additionally, it discusses historical lessons learned from maritime disasters, like the Titanic, which underline the need for better safety in engineering designs.
Detailed
Detailed Summary
This section delves into the concept of metacentric height, a critical factor in determining the stability of floating objects. The discussion begins with observations regarding the melting of ice beneath icebergs due to rising ocean temperatures, which can shift their center of buoyancy and lead to sudden collapses. This phenomenon was notably highlighted by the Titanic disaster, which resulted from inadequate knowledge about iceberg sizes and submerged portions, as only 1/8 of an iceberg is visible above water while 7/8 remains hidden.
The text draws parallels between the Titanic tragedy and modern engineering practices, stressing that advancements in technology, such as GPS and radar systems, allow for safer navigation and better understanding of maritime hazards. Furthermore, it is essential for engineers to prioritize safety over aesthetics, particularly in ship design.
The section transitions into the practical application of metacentric height through experiments that measure the stability of floating objects. By discussing fluid mechanics and the behavior of liquids in accelerating or rotating systems, the importance of understanding buoyant forces is reinforced in the context of engineering solutions. Through this lens, fluid statics principles, such as Archimedes' Principle, relate to modern engineering, thereby bridging the gap between theoretical knowledge and practical application.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Metacentric Height
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
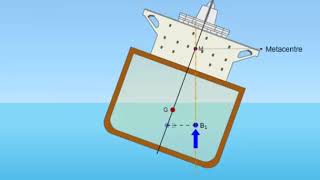
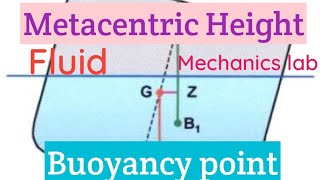
So let us look at simple experiment, metacentric height experimental setups with just balancing the weight we can measure the metacentric height of a floating object like this and this type of facilities are there any fluid mechanics lab, you can just measure the metacentric height and find out the stability of floating object.
Detailed Explanation
Metacentric height is an important concept in fluid mechanics that relates to the stability of floating objects, such as boats or icebergs. In simple experimental setups, we can determine the metacentric height by balancing weight. This height gives us a measure of the vessel's stability when it is tilted. If the metacentric height is greater, the floating object is more stable and less likely to flip over.
Examples & Analogies
Imagine a seesaw. If one side is heavier (the metacentric height is low), it tilts easily which means it lacks balance. If both sides are evenly matched (higher metacentric height), it remains stable. Similarly, boats need a higher metacentric height to ensure they don’t tip over easily in the water.
Fluid Statics and Acceleration Effects
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now let us come it to the another component on fluid statics that means fluid at the rest. But we are looking it a rigid body motions. That means what it happens that if I have a half filled liquid containers. That means I have a half filled liquid containers. It has a free surface and this is the containers. If I accelerate it with acceleration a. Okay, I have a tank and I am just accelerating with acceleration a.
Detailed Explanation
Fluid statics make it possible to analyze fluids at rest, but when we accelerate a container with liquid, the behavior of the liquid surface changes. When moving a half-filled container, the free surface of the liquid will initially slosh due to the acceleration but eventually stabilize into a new shape depending on the acceleration applied. This phenomenon can be analyzed mathematically, revealing how the behavior of the liquid mimics that of a rigid body under specific conditions.
Examples & Analogies
Imagine driving a car with a half-filled cup of water. When you accelerate quickly, the water sloshes around but then settles to a new level when you stop accelerating. The shape the liquid adopts reflects the direction of the acceleration, just like the liquid in our accelerating tank.
Pressure Gradient During Acceleration
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So the basically what you can try to know it that as we move with a constant acceleration, the free surface changes, the pressure diagram changes it and that what equate with two force component, one is particle acceleration component and other is the gravity force component.
Detailed Explanation
When we apply a constant acceleration to a fluid, the free surface becomes inclined. This incline reflects the balance between the gravitational force acting downwards and the inertial force due to the acceleration. The relationship between these forces creates a pressure gradient within the fluid that can be analyzed mathematically. The angles and variations of these forces help in designing various fluid systems and enhance our understanding of fluid behavior under acceleration.
Examples & Analogies
Think of a bottle of soda in a car. As you speed up, the soda presses against the back of the bottle due to the inertial force, and when you stop suddenly, it might foam up and spill out! This happens because the pressure on the liquid adjusts according to the car’s movement, showing the principle we discuss.
Rotational Dynamics of Liquids
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now we are talking about the rotations. If you look it any chemical industry, the dairy industry many times we do the mixing of the two liquids. What we do it we actually do the uniform rotations of the liquid contents okay.
Detailed Explanation
In many industries, liquids are mixed using rotational techniques. During uniform rotation, the liquid behaves as a solid, leading to no velocity gradients and shear stresses within the liquid. The resulting shape of the liquid surface will be parabolic due to the centrifugal force acting outward, while gravity pulls down, balancing these forces allows us to predict the behavior of the liquid under rotation.
Examples & Analogies
Think about stirring a pot of soup. When you stir it quickly, the soup forms a smooth surface in the center. Even though it’s still fluid, the rapid motion causes it to behave more like a solid disk, illustrating how rotation affects liquid dynamics.
Practical Application of Metacentric Height
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So what my point is to say that so, as an engineer who may built a big interior design, expensive ship but also you should look it the safety of the ship.
Detailed Explanation
The discussion on metacentric height emphasizes the importance of safety in engineering, particularly in ship design. Engineers must consider stability through the metacentric height rather than focusing solely on aesthetic or luxury aspects such as interior design. This lesson is vital in preventing accidents in maritime operations, similar to the fate of vessels like the Titanic, which underestimated the dangers of icebergs due to lack of understanding of buoyancy and stability.
Examples & Analogies
Like building a tall building, engineers should prioritize sturdy foundations and safety features instead of just beautiful glass facades. The same way ships should be built with a focus on stability to survive in the ocean, rather than just be designed to look good.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Metacentric height - A critical measurement for stability in floating objects.
-
Center of buoyancy - Influences how floating structures behave in water.
-
Buoyant force - Key to understanding how objects float.
-
Specific gravity - Important in comparing densities of various materials.
-
Archimedes' Principle - Foundation of fluid mechanics related to buoyancy.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
An iceberg floats with 1/8 of its volume above water and 7/8 submerged, demonstrating metacentric height in real life.
-
The design of modern ships integrates metacentric height calculations to ensure safe navigation.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Iceberg floating, just a bit, beneath the water, it does sit.
📖 Fascinating Stories
-
Imagine an iceberg, majestic yet hidden. Only a small part shows, but its true size is forbidden. It warns ships of unseen dread, as many learned when the Titanic led.
🧠 Other Memory Gems
-
Mighty Icebergs Stand Tall For Safety (Metacentric, Iceberg, Stability, Titanic, Force).
🎯 Super Acronyms
BASIC
- Buoyant must always stay in center.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Metacentric Height
Definition:
The distance between the center of buoyancy and the metacenter, indicating the stability of a floating object.
-
Term: Center of Buoyancy
Definition:
The center of mass of the displaced fluid, which influences the stability of a floating body.
-
Term: Buoyant Force
Definition:
An upward force exerted by a fluid, opposing the weight of an object immersed in it.
-
Term: Specific Gravity
Definition:
The ratio of the density of a substance to the density of a reference substance, typically water.
-
Term: Archimedes' Principle
Definition:
A principle stating that a body immersed in fluid experiences a buoyant force equal to the weight of the fluid displaced.