Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Iceberg Stability
Unlock Audio Lesson
Today, we'll discuss the stability of icebergs. Can anyone tell me why only a small portion of an iceberg is visible above water?
I think it's because ice is less dense than water, like how ships float.
Exactly! About 1/8 of the iceberg is above water, while the remaining 7/8 are underwater. Now, what happens if melting occurs underwater?
It changes the center of buoyancy, right? This could lead to instability?
Correct! When the center of buoyancy shifts negatively, it can cause the iceberg to collapse. Think about the Titanic—what can we learn from that?
We need to understand how icebergs work to ensure ship safety.
Well summarized! Always consider safety in large constructions as well. Let's take a closer look: what is metacentric height?
Rigid Body Motion in Fluids
Unlock Audio Lesson
Let’s connect iceberg stability with fluid motion. What happens in a half-filled liquid container when it's accelerated?
The liquid would slosh around initially, but then it would settle.
Good observation! After a while, a new free surface forms. How does that help in understanding rigid body motions?
It means the fluid acts like a solid, right?
Exactly! There are no shear stress formations, only pressure gradients. Can anyone explain how we calculate this pressure?
By considering the forces acting on the liquid—gravity and acceleration?
Spot on! Let’s summarize: the pressure gradient is adjusted based on the acceleration and gravity. Very important for practical applications!
Centrifugal Forces and Rotating Liquids
Unlock Audio Lesson
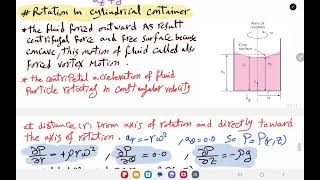
Now, let's discuss centrifugal forces. When we rotate a liquid in a container, what shape does the liquid take at the surface?
It forms a parabolic shape, right?
Yes! And how does this relate to pressure?
The pressure changes along the height due to centrifugal acceleration?
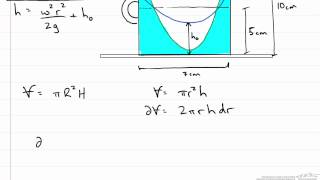
Exactly! The pressure increases towards the bottom. Can someone derive the equation governing this?
We can set up the gradient in terms of density and the centrifugal force.
Perfect! Remember, understanding these principles is crucial for engineers, especially in industries like dairy. Now, let’s wrap it up by summarizing what we covered today.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The chapter elaborates on the dynamics of large icebergs, explaining how their stability is compromised by underwater melting. It transitions into the principles of rigid body motion, particularly in half-filled liquid containers under acceleration and scenarios with uniform rotations, detailing how these factors affect fluid behavior and pressure distribution.
Detailed
In this section, we first explore the phenomenon of iceberg stability, emphasizing the significance of the submerged portion of ice and the effects of underwater melting, which can lead to sudden collapses. The discussion includes historical references, such as the Titanic disaster, highlighting the consequences of underestimating iceberg dynamics. The section then moves on to the rigid body motion of liquids, focusing on half-filled containers undergoing acceleration. It explains how the fluid eventually stops sloshing and behaves as a solid body, resulting in a new free surface configuration. Key equations governing pressure changes due to gravity and acceleration are introduced, including the implications of centrifugal forces in rotating systems. The section concludes with an exploration of experimental setups that can show these behaviors, emphasizing the importance of accurate measurement and understanding of fluid mechanics.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Understanding Liquid Behavior in Accelerating Containers
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
If I have a half filled liquid container. It has a free surface and this is the container. If I accelerate it with acceleration a. Okay, I have a tank and I am just accelerating with acceleration a. [...] the liquid will have a different free surface and after that there will be no change of the velocity gradients and no shear strain formation.
Detailed Explanation
When a liquid container is accelerated, the liquid inside undergoes a behavior change. Initially, if the container is moving, the liquid sloshes around. However, once the acceleration is steady, the liquid settles into a new free surface, making it behave as if it were a rigid body. This means that the liquid is no longer changing shape internally due to shear forces, as no velocity gradients are present. Thus, it behaves uniformly.
Examples & Analogies
Imagine riding a car on a straight road. When you accelerate suddenly, you feel your body push back against the seat, just like how the liquid sloshes. But if the car moves at a constant speed, your body feels stable, similar to how the liquid settles at a new surface.
Forces Acting on an Accelerating Fluid
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So the problem is now it is quite simplified and it becomes a just as if a rigid body motions. That means, the liquid is there but we can consider because there is no shear stress, only this have. That means what are the force components are there? The force components are one is force due to the pressure, gravity force and force due to this acceleration component.
Detailed Explanation
In the context of the fluid in an accelerating container, there are three main forces acting: gravitational force, pressure force, and the force due to acceleration. Since there is no shear stress involved in uniform acceleration, the fluid can be treated as a static body with respect to these forces. The pressure gradient is directly influenced by both gravitational pull and the acceleration of the fluid.
Examples & Analogies
Think of a game where you fill a balloon with water and then run. When you stop running, the water in the balloon settles and takes the shape of the balloon. The forces acting on the water (gravity pulling down and your running causing pressure) are similar to the forces on the fluid.
Pressure Distribution in Accelerating Containers
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now if you look at this interesting equations, which is the simplified equations what we got it for this the liquid containers that you can see that the change of the pressure gradient and (g – a), are the pressure gradient acts in the direction of (g – a).
Detailed Explanation
The pressure within an accelerating fluid behaves such that the pressure gradient (change in pressure with height) is influenced by the difference between the gravitational force and the accelerating force. This understanding allows for predicting how the fluid pressure changes as the container accelerates, with the direction of the pressure gradient being aligned against the resultant force (gravity minus acceleration).
Examples & Analogies
Consider mixing drinks in a tilted cup; the liquid will rise on one side and lower on the other due to gravity and the cup's tilt. Just like that, in an accelerating container, the pressure distribution changes due to forces acting in different directions.
Effects of Rotational Motion on Fluid Shape
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now we are talking about the rotations. If you look it any chemical industry, the dairy industry many times we do the mixing of the two liquids. What we do it we actually do the uniform rotations of the liquid contents okay. [...] it is again as if like a rigid body motions.
Detailed Explanation
When liquid containers rotate uniformly, the contents experience a centrifugal force that changes the distribution of the liquid's surface. Over time, this motion leads to a steady shape that mimics rigid body behavior, meaning there are no internal velocity gradients causing movement within the fluid, similar to how a solid body behaves.
Examples & Analogies
Think about the Earth spinning. Water in a large rotating drum experiences centrifugal force moving it outward, leading to a stable surface similar to how the ocean's water levels are influenced by gravitational pull and the rotation of the Earth.
Understanding Centrifugal Forces in Rotating Fluids
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
If you look it that, if you have a constant translations accelerations or uniform rotations, the gradient of P is equal to rho times of the vectorical difference between acceleration due to gravity and the centrifugal acceleration component.
Detailed Explanation
In a rotating frame, the pressure gradient relates to the density of the fluid multiplied by the net effect of gravitational acceleration and the centrifugal acceleration. This relationship helps in understanding how pressure differences create potential flows within the fluid body.
Examples & Analogies
Consider giving a spin to a merry-go-round. The children on the edge feel pushed outward due to centrifugal forces, just as fluids experience pressure variations in rotating systems, influenced by gravitational forces at play.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Stability of Icebergs: The portion of ice visible above water is much smaller than the submerged part, affecting stability due to factors like underwater melting.
-
Rigid Body Motion: When accelerated, fluids can behave like rigid bodies, with no shear stress, resulting in new free surface configurations.
-
Centrifugal Forces: These forces act on rotating fluids, causing parabolic surfaces and impacting pressure distributions within containers.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
The Titanic disaster serves as a historical example of not understanding iceberg dynamics and the importance of iceberg design and navigation.
-
When a container of liquid accelerates, it eventually reaches a state where the liquid behaves similarly to a solid body, demonstrating how acceleration affects fluid stability.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Icebergs drift with grace and might, Seven eighths are hid from sight.
📖 Fascinating Stories
-
Imagine a ship sailing strong, unaware of the ice lurking long below the surface, leading to unforeseen disaster.
🧠 Other Memory Gems
-
B.U.I.O.Y. - Buoyancy, Underwater melting, Iceberg danger, Observe metacentric, Yield to forces.
🎯 Super Acronyms
C.A.F. - Centrifugal Acceleration Forces impacts shape and pressure.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Center of Buoyancy
Definition:
The center of mass of the displaced fluid that is equal to the mass of fluid displaced by the submerged portion of an object.
-
Term: Metacentric Height
Definition:
The height of the metacenter above the center of gravity of a vessel; a key factor in determining the stability of floating objects.
-
Term: Centrifugal Force
Definition:
An apparent force that acts on an object moving in a circular path directed away from the center of rotation.
-
Term: Pressure Gradient
Definition:
The rate of pressure change in a fluid, which can be influenced by acceleration and gravity.
-
Term: Free Surface
Definition:
The surface of a liquid in a container that is free to move, influenced by external forces.