Assumptions and Conditions
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Bernoulli's Equation
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today, we will delve into Bernoulli's equation, a cornerstone in fluid mechanics that helps us understand how energy and pressure vary within a flowing fluid. Can anyone tell me why understanding these variations is important?

It's crucial for predicting how fluids behave in different environments, like pipelines and airfoils.

Yes! It helps engineers design systems that use fluid flow efficiently.

Exactly! Bernoulli's equation is essentially a statement of conservation of energy principle. We need to remember that for it to be applicable, several assumptions must be made.
Key Assumptions of Bernoulli's Equation
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

The first assumption is that fluid flow must be steady, meaning the velocity at any point does not change with time. What does this imply for fluid systems?

It means that the flow rates, pressures, and velocities should remain constant over time at any given point.

Then there's the incompressibility condition, right? That means the fluid density remains constant?

Correct! And finally, we assume the flow to be frictionless or inviscid. Why is this assumption important?

If friction were present, energy losses would occur, complicating our calculations.

Right! So these assumptions simplify the analysis and help us predict outcomes effectively.
Application and Importance of Understanding these Assumptions
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Let's talk about applications. How does understanding these assumptions help engineers?

It allows them to model real scenarios like airflow over aircraft wings or water flow in pipes.

But they have to consider any potential errors due to these assumptions, especially in real-life applications.

Exactly! While Bernoulli's equation provides a simplified view, engineers must account for surprises that might arise while applying these principles in chaotic environments.
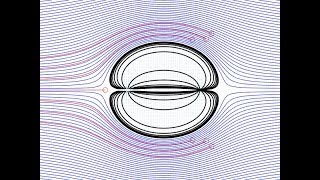
Pressure and Velocity Fields
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now, another crucial aspect of Bernoulli's equation is the relationship between pressure and velocity fields. What connection can you observe?

I remember from class that when velocity increases, pressure decreases, and vice versa.

This is in line with the continuity equation, where mass flow must remain constant!

Exactly! This inverse relationship is significant for many applications, such as understanding blood flow in vessels or air currents over wings.
Recap of Key Concepts
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

To wrap up today's learning, let's summarize the key points. Can anyone share the assumptions we've discussed regarding Bernoulli's equation?

Steady flow, incompressible fluid, and frictionless flow.

And the importance of pressure and velocity fields in determining the behavior of fluids.

Well done! Remember these concepts as we continue exploring fluid mechanics. They form the foundation of our understanding in this field.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
In this section, the focus is on understanding the significance of Bernoulli's equation, the assumptions necessary for its application, and the relevance of fluid flow fields such as pressure and velocity. Additionally, it explores how these factors relate to energy conservation within fluid mechanics.
Detailed
In fluid mechanics, particularly while applying Bernoulli's equation, specific assumptions and conditions must be acknowledged to achieve accurate results. The flow must be considered to be incompressible, steady, and frictionless along a streamline. The interaction of pressure and velocity fields is pivotal as they represent the two significant facets of fluid dynamics being explored. Understanding these conditions enables engineers and scientists to analyze various fluid-related situations effectively, ensuring energy conservation principles are maintained. This section provides a foundation by describing how these assumptions help in simplifying complex fluid systems and enhancing the correctness of fluid dynamics results, especially in real-world applications.
Youtube Videos





![Common assumptions in fluid mechanics [Fluid Mechanics #3b]](https://img.youtube.com/vi/kimMbNP9DrY/mqdefault.jpg)



Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Bernoulli's Equations
Chapter 1 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
The Bernoulli’s equation is another conclusion by Bernoulli is used in different fluid flow problems. In short, I can tell you that these equations help us to solve the many fluid flow problems by considering energy considerations or a linear momentum equation.
Detailed Explanation
Bernoulli's equations are fundamental in fluid mechanics, enabling us to analyze various fluid flow situations. They are derived from energy conservation principles that relate the speed of a fluid to its pressure at different points along a streamline. Essentially, the equation allows for calculations of fluid dynamics by considering how energy is distributed within the system. It emphasizes how variations in speed can lead to differences in pressure, which is crucial for solving practical engineering problems.
Examples & Analogies
Imagine riding a bike down a hill—when you pedal hard (increasing your velocity), you exert less force on the brakes (pressure decreases). Similarly, in fluid dynamics, an increase in fluid speed leads to decreased pressure. This principle is why aerodynamic designs, like airplane wings, make use of Bernoulli's equation to create lift that allows flight.
Key Assumptions of Bernoulli's Equation
Chapter 2 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
But many of the times you do not know when you apply the Bernoulli equations, what are the assumptions behind that? Is it energy conservation equations or linear momentum equations.
Detailed Explanation
When applying Bernoulli's equation, certain assumptions are made to simplify the fluid flow problem. These include: 1) The flow is steady (properties at a point do not change over time). 2) The fluid is incompressible (density remains constant). 3) The flow is frictionless (no energy loss due to viscosity). 4) Streamlined flow (all particles follow smoothly along the streamline). Understanding these assumptions is crucial as they define the limitations of the equation and inform the user when it's appropriate to apply them.
Examples & Analogies
Think of a smooth slide at a playground. For a child to slide effortlessly, there needs to be a certain height (potential energy) and no friction from their clothes or the slide's surface. If the slide becomes rough or if the child starts at different heights or positions, the experience changes dramatically. Similarly, Bernoulli’s assumptions outline conditions for ideal fluid behavior, helping predict flow outcomes accurately.
Applications of Bernoulli's Equation
Chapter 3 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
With this brief introductions, let I go to the today contents of the lectures. We will start with applications ... we will solve some of the simple example problems using Bernoulli equations.
Detailed Explanation
Bernoulli’s equation is not just theoretical; it has practical applications in numerous fields. It aids in designing various engineering systems such as airfoils in aircraft, water distribution systems, and predicting weather phenomena. By analyzing pressure and velocity changes in real-world scenarios—like predicting how fast a river will flow or how efficiently a plane will fly—engineers can make informed design choices. The practical exercises will further solidify understanding by illustrating how the equations apply to analyze real-life situations.
Examples & Analogies
Consider how they design footballs for different weather conditions. When designing a football for stormy weather, engineers must account for how windy conditions affect the ball's flight path (akin to how Bernoulli’s equations address pressure and velocity changes). By applying these fluid dynamics concepts, engineers can create a ball that maintains its trajectory, offering the best performance despite unpredictable elements.
Contributions of Daniel Bernoulli
Chapter 4 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
I can say it the contributions of Daniel Bernoulli ... those who are interested, I can just encourage you please visit Wikipedia of Daniel Bernoulli and his contributions.
Detailed Explanation
Daniel Bernoulli made significant contributions to fluid dynamics through his formulation of what we now call Bernoulli’s equation. He studied the relationship between fluid speeds and pressures, paving the way for modern applications in various fields like aerodynamics, hydraulics, and even medical devices that monitor blood flow. His work is foundational in understanding how fluids behave in different environments, particularly how they interact with forces in motion.
Examples & Analogies
Bernoulli’s principle explains why an airplane can soar high into the sky. The shape of the wings is designed in such a way that air moves faster over the top surface than the bottom, creating lift due to the pressure difference—exactly what Bernoulli theorized. Just as Bernoulli revolutionized our understanding of flight, his insights continue to influence modern engineering and technology.
Understanding the Relationship in Fluid Flow
Chapter 5 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
If you look it, there is a relationship between the pressure and the velocity. So, wherever the pressure increases, then the velocity decreases.
Detailed Explanation
This section highlights the inverse relationship between pressure and velocity in fluid mechanics. Essentially, when a fluid speeds up as it flows, the pressure decreases in the same region. This phenomenon is critical in various applications, from predicting how high buildings withstand wind pressure to optimizing the layout of piping systems in industries. It's a tangible demonstration of Bernoulli's equation, emphasizing the connection between speed and pressure in real-world fluid flow.
Examples & Analogies
Picture a garden hose with your thumb partially blocking the end. As you cover part of the opening, the speed of the water increases, but the pressure at the hose opening decreases—this is the principle of Bernoulli at work. Understanding this relationship helps gardeners maximize water pressure and efficiency when watering plants.
Key Concepts
-
Steady Flow: The condition where the fluid's velocity remains constant over time at any point.
-
Incompressible Flow: A scenario where fluid density is assumed to be constant.
-
Frictionless Flow: Refers to an ideal flow situation in which all viscous forces are neglected.
Examples & Applications
An airplane wing generates lift due to differences in pressure and velocity above and below the wing as explained by Bernoulli's principle.
A garden hose nozzle increases the velocity of water as it exits due to a decrease in cross-sectional area, illustrating the relationship between pressure and velocity.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
In flow so steady and smooth like a song, Pressure drops as velocity goes strong.
Stories
Imagine a small stream where stones meet water. As the water flows faster around a stone, it exhibits lower pressure—this is how Bernoulli's principle unfolds in nature!
Memory Tools
Remember 'S.I.F' for the assumptions: Steady, Incompressible, Frictionless.
Acronyms
P.V.E for Pressure, Velocity, Energy relationship in Bernoulli's equation.
Flash Cards
Glossary
- Bernoulli's Equation
A principle that describes the conservation of energy in fluid flow, relating pressure, velocity, and height.
- Steady Flow
A type of fluid flow where the velocity of the fluid remains constant over time at any given point.
- Incompressible Flow
A flow in which the fluid density remains constant regardless of pressure changes.
- Frictionless Flow
An idealized flow with no viscosity, meaning no energy is lost due to friction.
- Velocity Field
A representation of the velocity of a fluid at every point in space.
- Pressure Field
A representation of the pressure exerted by a fluid at every point in space.
Reference links
Supplementary resources to enhance your learning experience.
