Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Bernoulli's Equations
Unlock Audio Lesson
Today we are discussing Bernoulli's Equations, a key principle in fluid mechanics. Can anyone tell me what these equations represent?
They relate pressure, velocity, and elevation in fluid flows, right?
Exactly! They reflect the conservation of mechanical energy within flowing fluids. What assumptions do we make when we apply Bernoulli's Equations?
We assume steady, incompressible, and frictionless flow.
Well done! These assumptions are crucial for the validity of the equations. Remember: SIW - Steady, Incompressible, and Frictionless.
What happens if we don't meet these assumptions?
Great question! If the flow isn't steady or if viscosity is significant, Bernoulli's Equations may not hold true. Let's keep this in mind as we explore more.
Applications of Bernoulli's Equations
Unlock Audio Lesson
Now, let's explore some applications. Who can give examples where we might use Bernoulli's equations?
It’s used in checking the flow of blood in veins.
Right! Blood flow relates velocity and pressure. As speed increases, pressure drops—a real-life application of Bernoulli’s observations.
What about flying? Does Bernoulli also apply there?
Absolutely! The shape of the aircraft wing generates a pressure difference that helps lift, thanks to Bernoulli's principle.
So, the airplane wings are shaped to create different velocities above and below?
Spot on! The curvature causes air above to move faster, lowering pressure and causing lift.
Theoretical Derivation Process
Unlock Audio Lesson
Let us now dive into how we derive Bernoulli’s Equation. What do we start with when analyzing a fluid system?
We apply conservation of mass and momentum, right?
Correct! We look at the control volume and apply the mass conservation principle first. What does that mean?
It implies the mass entering the control volume must equal the mass leaving.
Precisely! Then we incorporate momentum, considering net forces acting before integrating them to derive the equation.
Can you remind us about the pressure and velocity relationships during this derivation?
Sure! As velocity increases, pressure decreases. This relationship is central to our analytical framework. That's Bernoulli's insight!
Practical Implications of Assumptions
Unlock Audio Lesson
We need to understand the implications of violating Bernoulli’s assumptions. What happens in viscous fluids?
Then energy gets lost to friction, and the equation isn’t valid anymore?
Exactly! That's why in real-world applications, such as pipes, we have to factor in these losses. What can we infer from this?
We must use correction factors to account for energy loss in practical applications.
Exactly! Always seek to model real-world applications accurately by acknowledging limitations in idealized equations.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
Theoretical derivations of Bernoulli's Equations highlight the relationship between pressure, velocity, and elevation in fluid fluid mechanics, emphasizing energy conservation and momentum equations. The section explains the necessary conditions for applying these equations and provides an overview of their significance in practical applications.
Detailed
Theoretical Derivations of Bernoulli's Equations
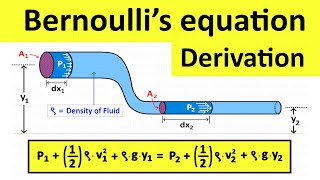
The derivation of Bernoulli's Equations is pivotal in understanding fluid mechanics, particularly in the conservation of energy within fluid flows. Bernoulli's Equations posits that along a streamline in a fluid flow, the total mechanical energy per unit weight remains constant. This section outlines the foundational assumptions that are critical to applying these equations, including:
- Steady Flow: The fluid properties at a point do not change over time.
- Incompressible Flow: The fluid density remains constant even with pressure changes.
- Frictionless Flow: There are no viscous effects acting within the fluid, meaning there is no energy loss due to friction.
The derivation proceeds with analyzing a control volume of fluid and applying the principles of mass and momentum conservation. Notably, it discusses how pressure, velocity, and elevation interact and maintain energy equilibrium in streamlined flows.
The section concludes by emphasizing the practical applications of Bernoulli's Equations in engineering, such as in the analysis of blood flow in vessels and the aerodynamics of aircraft wings. Understanding these principles allows for better modeling and predicting of fluid behavior in various contexts, reinforcing the significance of Bernoulli's contributions to modern fluid dynamics.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Bernoulli's Equation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The complete derivations of Bernoulli equation, which is very complicated. But very simple way, if I am to derive the Bernoulli equation, which gives us a relationship between the pressure, velocity, elevations in a frictionless flow which is very idealized conditions.
Detailed Explanation
The Bernoulli equation relates different properties of fluid flow, specifically pressure, velocity, and elevation, in conditions where there are no frictional forces acting on the fluid. This makes it easier to understand the balance of energy within the fluid.
Examples & Analogies
Imagine a water slide. When you start at a higher point, the water has stored potential energy due to its height. As it slides down, this potential energy is converted into kinetic energy (the speed of the water) at the lower point. Bernoulli's principle captures this energy transformation in fluid flow.
Assumptions in Deriving Bernoulli's Equation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
That means there is no shear stress component, okay. There is no shear stress component. We are assuming it that I have a simple, a streamline going on and along this streamline is flow is happening and these control volumes representing me a stream tube.
Detailed Explanation
The derivation of Bernoulli's equation makes two key assumptions: 1) the flow is frictionless, meaning there are no shear forces affecting the fluid motion, and 2) the flow is steady and along streamlines, which simplifies the analysis since the fluid properties can be assessed at specific points along the streamline.
Examples & Analogies
Think of a smooth, straight river. The water flows uniformly along its course without any obstacles causing friction. Just like in this river, when we analyze flow in pipes or over wings, we avoid complications from friction by assuming an ideal, frictionless flow.
Application of the Control Volume Concept
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Because of that, over the surface we do not have a mass influx coming into this control volume as well as there is no momentum flux coming into this control volume through this surface.
Detailed Explanation
In considering a control volume—a defined space through which fluid moves—we assume that no mass is entering or leaving the volume through its side surfaces. This simplification allows us to focus only on the inflow and outflow, making it easier to apply conservation principles.
Examples & Analogies
Picture a water balloon. If you only look at the water inside the balloon, you can analyze how it shifts as you squeeze it without worrying about any water entering or leaving—it’s self-contained, similar to how we view control volumes in fluid dynamics.
Equations of Motion and Energy Balance
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now I am applying the linear momentum equations in streamline directions or streamwise directions. So sum of the force should be equal to the rate of change of the momentum in the control volume.
Detailed Explanation
By applying Newton’s second law, the sum of forces acting on the control volume is equal to the rate of change of momentum within that same control volume. This relationship forms the basis of the derivation for Bernoulli's equation, linking forces, momentum, and flow dynamics.
Examples & Analogies
Imagine pushing a swing. The force you apply changes the swing's momentum, making it move faster. Similar principles apply in fluid motion, where forces (like pressure differences) cause changes in the flow's momentum.
The Components of Bernoulli's Equation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Whenever you have a streamtube or the steamlines, any point you consider 1, 2, 3, 4. If it is a fictional loss, there is no energy losses in these 1, 2, 3, 4 points, we will have a total energy becomes constant.
Detailed Explanation
In an ideal situation where no energy is lost (due to friction, for example), the total mechanical energy (including kinetic energy, potential energy, and energy due to pressure) remains constant throughout a streamline. This is the core idea behind Bernoulli's principle.
Examples & Analogies
Think of a roller coaster. When it climbs to the top (potential energy), then swoops down (kinetic energy), the total energy remains constant if we ignore air resistance and friction. This conservation of energy applies to fluid flows described by Bernoulli's equation.
Final Form of Bernoulli's Equation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So that means in fluid flow problems, we have three energy components, flow energy that is because of the pressures, kinetic energy and the potential energy.
Detailed Explanation
The final form of Bernoulli's equation combines the three types of energy: flow energy (related to pressure), kinetic energy (due to motion), and potential energy (due to elevation). The equation states that the sum of these energies is constant along a streamline if no energy losses occur.
Examples & Analogies
Consider a snowball rolling down a hill. At the top, it has potential energy (height). As it rolls down, that energy converts to kinetic energy (speed), but the total energy remains the same unless it melts or if there are losses in the form of friction.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Conservation of energy: Energy within a fluid is conserved along a streamline.
-
Pressure-velocity relationship: As velocity increases, the pressure within the fluid decreases.
-
Control volume: A defined area for analyzing the flow of fluids.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
The application of Bernoulli's Equation in aircraft wing design to create lift.
-
Analysis of blood flow where pressure changes can indicate health conditions.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Pressure high, velocity low, energy conserved, this you know.
📖 Fascinating Stories
-
Imagine fluid flows smoothly down a hill. The quick streams whiz past with low pressure, while the slow- meanderers hold onto higher pressure points. That's Bernoulli showing energy is conserved in its path!
🧠 Other Memory Gems
-
SIW: Steady, Incompressible, and Frictionless = Assumptions!
🎯 Super Acronyms
PVE
- Pressure
- Velocity
- Elevation – Key terms in Bernoulli’s Equation.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Bernoulli's Equation
Definition:
A principle in fluid dynamics that describes the conservation of energy in fluid flow, relating pressure, velocity, and elevation.
-
Term: Steady Flow
Definition:
A flow condition where fluid properties at a point do not change with time.
-
Term: Incompressible Flow
Definition:
A fluid flow in which the fluid density remains constant throughout.
-
Term: Frictionless Flow
Definition:
An idealized flow with no viscous forces acting within the fluid.
-
Term: Control Volume
Definition:
A defined volume in which the flow properties of a fluid is analyzed.