Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Bernoulli's Equation
Unlock Audio Lesson
Today, we will explore the Bernoulli equation, which helps us understand fluid behavior under various conditions. Can anyone tell me why energy conservation is critical in fluids?
I think it helps us predict how fluid will move.
Exactly! Energy conservation allows us to relate pressure, velocity, and elevation in flowing fluids. Remember, energy can neither be created nor destroyed. This is why we can apply Newton's laws to fluids as well.
What kind of applications does this equation have?
Excellent question! Bernoulli’s equation is used in everything from predicting blood flow rates to designing efficient piping systems in industries. It’s also utilized in aviation for lift calculation. Remember the acronym 'PVE' for Pressure, Velocity, and Elevation—it captures the core components we analyze.
How do we know the equation's assumptions?
Great point! We usually assume steady, incompressible, and frictionless flow. By ensuring these conditions, we can effectively apply the Bernoulli equation. Let's keep these in mind as we continue!
Experiments with Bernoulli's Equation
Unlock Audio Lesson
The fluid speed increases as the area gets smaller!
Exactly! This increase in fluid speed is accompanied by a decrease in pressure, in accordance with Bernoulli's principle. Can anyone think of real-world examples of this?
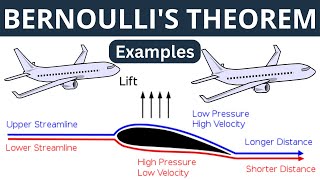
Like how planes fly? The air moves faster over the wings and creates lift!
Spot on! And in our experiments, by measuring the pressures at different points on the venturimeter, we validated this principle. Remember the phrase 'higher speed = lower pressure’ as you apply Bernoulli's equation!
Applications of Bernoulli's Equation
Unlock Audio Lesson
How do you think understanding Bernoulli's equation can help engineers?
It helps design safe buildings and aircraft!
Yes! Engineers must consider how wind can create high-pressure zones or low-pressure areas, especially in cyclone-prone regions. How about discussing cyclonic storms?
Cyclones can blow off roofs, right? It’s due to pressure differences!
Precisely! The rapid wind creates lower pressure over the roof compared to inside the building, resulting in lift forces. Always remember the impact of Bernoulli’s equation! 'LEAD' - Lift forces, Elevation, Application, and Design—key points to recall.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
This section provides insight into the applications and derivations of the Bernoulli equation, emphasizing the importance of energy considerations in fluid mechanics. Experiments conducted at IIT Guwahati validate these principles and highlight their applications in real-world scenarios such as aerodynamics and fluid flow in pipes.
Detailed
Bernoulli Experiment - Detailed Summary
The Bernoulli experiment revolves around the Bernoulli equation, which is fundamental in fluid mechanics. Initially, the chapter introduces the importance of Bernoulli's equations in solving fluid flow problems through energy considerations and linear momentum principles. The equations serve as a bridge between experimental data and theoretical frameworks, allowing for analysis in various fluid dynamics applications.
Key Points Covered:
- Applications of Bernoulli's Equation: An overview of how the equation applies to fluid mechanics problems, including areas such as blood flow dynamics and cyclone impacts.
- Theoretical Derivations: The section discusses the derivation of the Bernoulli equation, focusing on assumptions of steady, incompressible, and frictionless flow. It formulates relationships between pressure, velocity, and elevation within a control volume.
- Verification through Experimentation: The hands-on experiments conducted at IIT Guwahati involve measuring pressures in a venturimeter setup, illustrating fluid dynamic concepts in a visually interactive manner. By demonstrating how velocity and pressure relate, the experiments underpin the theoretical aspects of fluid mechanics.
- Real-world Applications: Practical illustrations show how Bernoulli's principles impact engineering contexts, such as aircraft lift generation and assessing damage during cyclones.
The comprehensive exploration of Bernoulli's equations equips students with a deeper understanding of fluid dynamics, paving the way for future studies in civil and mechanical engineering.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to the Bernoulli Experiment
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
This is what the verification of Bernoulli equations in fluid mechanics lab in IIT, Guwahati. If you look at these ones, it has two tubes to maintaining the contents in supply heads. There is two tanks are there, which is maintaining the supply heads and here, you have a venture meters.
Detailed Explanation
In this first chunk, we are introduced to the Bernoulli experiment conducted at IIT Guwahati. The purpose of this experiment is to verify the Bernoulli equations, which are fundamental in fluid mechanics. The setup involves two tubes that help maintain fluid in tanks, along with venturi meters, which are critical for measuring changes in fluid flow and pressure as the fluid moves through the apparatus.
Examples & Analogies
Consider this experiment similar to a water slide in a water park. The slide starts wide and then narrows down before expanding again. As water flows down the slide, it speeds up when entering the narrow part. Similarly, in this experiment, fluid speeds up and slows down in different sections, just like the water on the slide.
Understanding Venturi Meters
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So, there is a decreasing of the cross section area, then increasing. So, you have a converging zone, then it follows diversion gauge zone. So, if you conduct series of pressure meters which measure the pressures or the velocity head. If you look at that, this venture meters have a converging zones and the diverging zones.
Detailed Explanation
This section discusses the functioning of the venturi meters used in the experiment to measure the pressure and velocity of fluid flow. A venturi meter has two main parts: a converging zone where the cross-sectional area decreases and a diverging zone where it increases again. According to the principle of continuity and Bernoulli's principle, the velocity of the fluid increases as it passes through the narrower part of the meter, leading to a decrease in pressure.
Examples & Analogies
Think of drinking through a straw. When you put your thumb over the top of the straw, you create a narrow opening. The liquid inside the straw speeds up as it passes through that narrow section, just like the fluid in a venturi meter. Meanwhile, the pressure drops in that section, creating a situation where you can measure how fast the liquid is moving.
Pressure and Velocity Relationships
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
As we know, for a particular discharge, constant discharge, we can have a 11 pressure meters locations, where the radius are different, area of the flow is different, and the velocity will be different. That is what, so discharge is same since the area of the flow is varies.
Detailed Explanation
This part elaborates on the concept of discharge, which is the volume of fluid that passes through a given surface per unit time. Despite variations in the flow area and velocity at different points along the venturi meter, the discharge remains constant. The experiment measures the pressure at multiple points (11 locations) to demonstrate how these different areas impact fluid velocity, aligning with Bernoulli’s equation.
Examples & Analogies
It’s similar to a traffic situation: on a narrow road (smaller cross-section), more cars (higher velocity) pass through a point than on a broader road, where cars must slow down. Even though the number of cars (discharge) remains constant, the flow rate changes based on the width of the roadway.
Total Head Verification
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
This very simple thing, the discharge is equal to area into velocity. If area decreases velocity increases, that is what we got it. And we measure the velocity head, compute the velocity head, we have with a pressure head.
Detailed Explanation
This section discusses the verification of Bernoulli's principle by demonstrating that the total mechanical energy (or total head) of the fluid remains the same along a streamline. By measuring the pressure head and velocity head at different points, the experiment shows how variations in area affect both velocity and pressure, which is consistent with the conservation of energy as described by Bernoulli’s equation.
Examples & Analogies
Imagine a roller coaster: as the cart climbs to a high point (increased potential energy), it slows down (reduced velocity). As it descends, it speeds up (increased velocity) while losing potential energy. Just like in our experiment, where energy transforms between pressure and velocity, in the roller coaster, energy converts between potential and kinetic forms while conserving total energy.
Bernoulli's Head Consistency
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Equating these, if you look it, more or less the total head is the same, that means we have verified it that the total head along a streamline when going through a venture meters, it has the same value.
Detailed Explanation
In this chunk, it is emphasized that the computed total head (the sum of pressure head and velocity head) remains constant for the fluid moving through the venturi meter under steady conditions. This consistency serves as a practical verification of Bernoulli's equation, reinforcing the principle that energy is conserved within a fluid flow.
Examples & Analogies
Imagine filling a balloon with air. As you squeeze it (similar to narrowing the tube), the air inside compresses and its pressure increases. Conversely, if you let go, the balloon expands (wider area) and the pressure decreases, demonstrating how similar concepts of energy conservation apply even in simple everyday examples.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Energy Conservation: The principle that energy within a system remains constant despite changes in pressure and speed.
-
Incompressible Flow: A key assumption that fluid density does not change during flow.
-
Venturi Effect: The phenomenon where fluid speed increases and pressure decreases as the flow area narrows.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Example of blood flow in arteries: As blood travels through narrower vessels, it speeds up, causing drops in pressure.
-
Example of airplane lift: Faster airflow over the wing creates lower pressure, aiding in lift generation.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
When fluids flow through narrow ways, speed increases, pressure plays!
📖 Fascinating Stories
-
Imagine a river narrowing as it flows. The water rushes faster, creating a whirlpool. This shows how Bernoulli’s principle works—more flow, less resistance.
🧠 Other Memory Gems
-
Remember 'PEEK': Pressure, Energy, Elevation, Kinetic—key concepts of Bernoulli.
🎯 Super Acronyms
Use 'LEAD' to remember Lift forces, Elevation zones, Applications, and Design considerations in fluid mechanics.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Bernoulli Equation
Definition:
A principle that describes the behavior of fluid flow, relating pressure, velocity, and height.
-
Term: Venturimeter
Definition:
A device used to measure the flow rate of fluid through a pipe by observing pressure changes.
-
Term: Fluid Dynamics
Definition:
The study of fluids in motion and the forces acting on them.
-
Term: Incompressible Flow
Definition:
A flow regime where fluid density remains constant.
-
Term: Pressure Head
Definition:
The height of a column of fluid due to its pressure; an essential component of Bernoulli's equation.