Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Flow Classifications
Unlock Audio Lesson
Today, we're going to discuss flow classifications. Can anyone tell me why it’s important to classify different types of flows?
Isn't it because different types of flow have different properties and equations used for analysis?
Exactly! Classifying flow helps in choosing the right equations for analysis. So, what are the two main categories we typically talk about?
I think they are steady flow and unsteady flow?
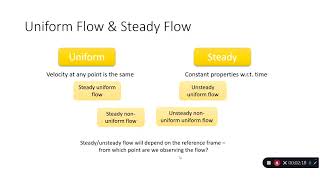
Right again! In steady flow, properties such as velocity and pressure at each point remain constant over time. Can anyone give me an example of unsteady flow?
Like the flow of a river after a heavy rain? It can change with rainfall.
Great example! Remember that in unsteady flows, properties can change with time. Let's move on to compressible vs. incompressible flow.
Compressible vs. Incompressible Flow
Unlock Audio Lesson
Now that we have discussed steady and unsteady flows, let's dive into compressible and incompressible flows. Who can explain what compressible flow is?
Is it when density changes significantly due to pressure changes, like in gases?
Exactly! While incompressible flow assumes a constant density, which we often apply to liquids because their density doesn't change much. Can anyone think of a scenario where we encounter compressible flow?
It happens often in gases, especially at high speeds, like in jet engines.
Correct! And understanding these differences is key because it affects how we apply Bernoulli's equation. Is everyone clear on these concepts?
Dimensionality in Fluid Flow
Unlock Audio Lesson
Let’s talk about dimensionality in fluid flows, specifically one-dimensional flow. Why do you think we use one-dimensional flow assumptions?
Because it simplifies the calculations by looking at fluid properties in just one direction?
Exactly! This allows us to apply equations like Bernoulli's more easily. What happens in a two-dimensional or three-dimensional flow?
It gets more complicated because you have to consider changes in multiple directions.
That's correct! And in most engineering problems, we often start with the one-dimensional assumption for simplicity.
Application of Flow Classifications
Unlock Audio Lesson
So how do these classifications ultimately help us in engineering tasks?
They guide us to the right equations and methods for our analysis based on the flow type.
Perfect! And can someone give an example of applying these flow classifications in a real project?
When designing bridges, knowing the water flow type helps determine how to protect the structure.
Correct! Knowing whether you're dealing with steady or unsteady flow can make a big difference.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In this section, we explore the fundamental classifications of fluid flow, detailing terms like steady flow, unsteady flow, compressible flow, and incompressible flow. These classifications help engineers properly analyze fluid behavior and apply relevant equations, such as Bernoulli's equation, to various engineering problems.
Detailed
Detailed Summary
The flow classifications in fluid mechanics are essential for understanding the behavior of fluids under various conditions. This section covers:
Key Classifications:
- Steady vs. Unsteady Flow:
- In steady flow, the fluid properties at any point do not change over time. It maintains a consistent velocity and pressure at any given point during the analysis. In contrast, an unsteady flow experiences temporal changes in these properties, requiring more complex analysis tools.
- Compressible vs. Incompressible Flow:
- Compressible flow occurs when changes in pressure and temperature are significant enough to affect fluid density, commonly seen in gases at high velocities. Incompressible flow, on the other hand, assumes that fluid density remains constant, typically applied to liquids where variations are negligible.
- Dimensional Considerations:
- The classification also includes one-dimensional (1D) flow, where fluid properties vary only along one direction, simplifying analysis using Bernoulli’s equation.
Importance of Classifications:
The significance of flow classifications is paramount as they determine the appropriate theoretical frameworks and equations, like Bernoulli's equation, to solve real-world fluid mechanics problems effectively.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Flow Classifications
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now let us look at the flow classifications or the simplifications that in this case we have considered one-dimensional steady incompressible or compressible that is what we will discuss just a bit here. We have a stream tube, fixed control volume, okay.
Detailed Explanation
This chunk introduces the concept of flow classifications in fluid mechanics. It emphasizes the importance of various types of flow, notably one-dimensional flow which can be either steady or unsteady, and compressible or incompressible. A 'stream tube' is mentioned, which refers to a series of streamlines defining the flow of fluid, and a 'fixed control volume' is a chosen region in which we analyze the fluid's behavior.
Examples & Analogies
Think of a garden hose. When you turn on the hose and let the water flow out of it, the water flows in a specific direction, and you can imagine the flow lines as a series of connected paths inside the hose. This is like the 'stream tube' concept. If you pinch the hose to make the water flow faster, you're creating a scenario that can be classified as one-dimensional steady flow.
Characteristics of Stream Tubes
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The advantage of the stream tube is that there is no flow across this stream tube, because that is what the definitions of the streamlines, there will be no flow component to normal to this part, because all the flow components will be tangential to the spot.
Detailed Explanation
Stream tubes have a critical property: there is no flow of fluid across them. This means the fluid moves solely along the direction of the streamlines without any perpendicular flow. The streamlines represent the path of individual fluid elements, ensuring that fluid either flows into or out of the stream tube without mixing with other flows.
Examples & Analogies
Imagine a narrow river surrounded by banks. The shape of the river can be thought of as a stream tube, where the water flows straight along its path without jumping over the banks. Any debris in the water follows the same flow and cannot cross over to different areas, similar to how fluid elements in a stream tube behave.
Control Volume Concept
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Because of that, we do not have any flow pass through perpendicular to the surface. The flow comes from this direction and goes from this.
Detailed Explanation
The concept of a control volume in fluid mechanics is linked closely with stream tubes. By defining a 'control volume', we identify a specific region through which we analyze the mass inflow and outflow without considering flow across its surface. This simplification helps in applying conservation laws such as mass and momentum more easily.
Examples & Analogies
Consider a balloon filled with air. The surface of the balloon acts as a control volume. Air molecules can move in and out of the balloon, but they cannot pass through the balloon's rubber surface. When you squeeze the balloon, you see the air inside being compressed, demonstrating how we can analyze changes within our defined control volume without worrying about external airflow.
Assumptions in Flow Analysis
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now if you look it, since there is no friction is there, okay. So, we can easily consider is that shear stress is equal to zero.
Detailed Explanation
When analyzing fluid flow in a stream tube, some assumptions simplify the calculations. One key assumption is that there is no friction, meaning shear stress can be considered zero. This allows us to analyze the ideal conditions under which the fluid flows, making it easier to derive equations of motion and energy conservation.
Examples & Analogies
Think about a perfectly smooth slide at a playground. Without any friction, a child would glide down effortlessly, illustrating how idealized conditions help clarify the underlying physics. In real-world situations, friction exists but considering it to be zero simplifies our initial understanding of fluid behavior.
Applications of Flow Classifications
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So, whenever you have a streamtube or the steamlines, any point you consider 1, 2, 3, 4. If it is a fictional loss, there is no energy losses in these 1, 2, 3, 4 points, we will have a total energy becomes constant.
Detailed Explanation
In applications of fluid mechanics, particularly when analyzing flow through stream tubes, we often assume that energy is conserved throughout the flow (unless there are losses due to friction or turbulence). This means that the total energy—composed of potential energy, kinetic energy, and flow energy—remains constant along a streamline under ideal conditions.
Examples & Analogies
Using the slide analogy again, if a child goes down without any obstacles or friction, they reach the bottom with a certain energy that has converted from potential to kinetic. Similarly, in fluid mechanics, as fluid moves through a streamline, its energy transformations can be predicted based on these conservation principles.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Steady Flow: Fluid properties that remain constant over time.
-
Unsteady Flow: Properties that vary over time.
-
Compressible Flow: Density varies significantly due to changes in pressure.
-
Incompressible Flow: Density remains constant.
-
One-Dimensional Flow: Simplifies analysis by assuming variation in one direction.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Water flow in a well-designed pipeline can be treated as incompressible flow.
-
Air flowing over an airfoil at low speeds can often be considered incompressible.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Steady and steady, flows that stay, Unsteady flows change, night and day.
📖 Fascinating Stories
-
Imagine a calm river, steady and clear, and a raging flood that changes each year.
🧠 Other Memory Gems
-
To remember flow types, think 'SUC'—Steady, Unsteady, Compressible.
🎯 Super Acronyms
Use 'SIC' for remembering Steady, Incompressible, Compressible flows.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Steady Flow
Definition:
A type of flow where fluid properties at any point do not change with time.
-
Term: Unsteady Flow
Definition:
A flow where fluid properties change with time.
-
Term: Compressible Flow
Definition:
Flow where density changes significantly due to pressure or temperature variations.
-
Term: Incompressible Flow
Definition:
Flow where fluid density remains constant.
-
Term: OneDimensional Flow
Definition:
Flow characterized by variations in one direction, simplifying analysis.