Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Laboratory Measurement Techniques
Unlock Audio Lesson
Today, we're looking at how we measure the permeability of soils in the lab. Can anyone tell me what the constant head permeameter is used for?
Isn't it for coarse-grained soils?
Exactly, Student_1! It's because the flow rate through coarse-grained soils can be measured accurately. Now, what about the falling head permeameter? Who can tell me the type of soil it's best suited for?
I think it's for fine-grained soils.
That’s right! In the falling head method, we measure how the total head drops over time. This variability in head needs to be understood well. What does that imply for typical experiments?
It suggests that we need to take multiple measurements over time.
Good observation, Student_3! Thus, the hydraulic gradient changes as the water flows through the soil, which we need to account for.
In summary, we're using two main methods: constant head for coarse soils and falling head for fine soils, adjusting our approach based on the type of soil to ensure accurate permeability readings.
Understanding the Continuity Equation
Unlock Audio Lesson
Now, let's connect Darcy's Law with the Continuity Equation. Who remembers what Darcy's Law states about flow?
It states that flow is proportional to the hydraulic gradient.
Precisely! And how do we express the flow rate mathematically?
It’s Q = k * A * (dh/dL) where k is permeability.
Correct, Student_1! When we apply the Continuity Equation to a small volume of soil, we look at the net flow in and out. How can we express this mathematically?
By using partial derivatives, right? Considering flow in all dimensions!
Exactly! Integrating these equations leads us to the flow equations. Can anyone explain why we need to consider isotropic conditions?
Because it simplifies the calculations if permeability is the same in all directions.
Great point, Student_3! When permeability varies, the equations become more complex.
To summarize, by combining Darcy's law with the continuity equation, we can model flow accurately in soils under different conditions.
Laplace Equation
Unlock Audio Lesson
Finally, let's talk about the Laplace equation. Can anyone tell me what it represents in the context of soil flow?
It describes the flow of water in more complex, three-dimensional spaces.
That's correct. And why is solving this equation important for geotechnical engineering?
It helps us understand how water moves through soils, which is critical for drainage design and more.
Excellent, Student_1! The methods can be graphical, analytical, or numerical. Adapting our approach is key. Why do you think different methods are used?
Because some problems are easier to visualize graphically, while others might need numerical calculations.
Spot on! In essence, understanding the Laplace equation and its implications allows us to analyze and solve complex flow problems in soils effectively.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The discussion focuses on the laboratory measurement of soil permeability through various methods such as constant head and falling head experiments, followed by the application of Darcy's Law and the Continuity Equation to describe two-dimensional and three-dimensional steady flow in soils.
Detailed
Combining Darcy's Law with Continuity Equation
In this section, we delve into the laboratory measurement of permeability, mentioning that the constant head and falling head permeameters are suited for coarse and fine-grained soils, respectively. The relationship between flow rate and head drop is established, leading to an understanding of seepage in soils through the construction of a continuity equation. By combining this equation with Darcy's Law, we derive a general flow equation. The significance of understanding isotropic materials, where permeability is constant in all directions, is discussed culminating in the formulation of the Laplace equation for two-dimensional flow. This framework also expands to three-dimensional flow situations. Mastery of these concepts is vital as they form the basis for analyzing groundwater movement and designing effective drainage and soil stabilization systems.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Understanding Seepage in Soils
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
A rectangular soil element is shown with dimensions dx and dz in the plane, and thickness dy perpendicular to this plane. Consider planar flow into the rectangular soil element. In the x-direction, the net amount of the water entering and leaving the element is...
Detailed Explanation
This chunk introduces the concept of how water flows through soils. It considers a small rectangular element of soil with specific dimensions (dx, dy, and dz). The flow in the x-direction is analyzed, looking at how much water enters compared to how much leaves this element. This basic identification of flow helps in establishing a balance needed to derive further equations. To ensure clarity, it's important to visualize this soil element as a small box where water enters from one side and exits from the other.
Examples & Analogies
Think of this rectangular soil element as a sponge placed in a tray of water. As water seeps into the sponge from the bottom (entering the element), it may also seep out from the sides, similar to how the water flows in and out of the soil.
Balancing Inflows and Outflows
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Similarly in the z-direction, the difference between the water inflow and outflow is...
Detailed Explanation
In addition to examining the flow in one direction (x-direction), this chunk discusses the z-direction, which is vertical. Here, the principle remains the same—comparing how much water enters the element versus how much exits. This method effectively sets up an equation accounting for both directions, creating a balance that is necessary for analyzing fluid flow in soil.
Examples & Analogies
Imagine a tall glass of water: if more water is added from the top than is seeping out from the bottom, the water level will rise. Balancing inflows and outflows controls whether the glass overflows, just as managing water in soil helps predict dry or saturated conditions.
Introducing the Continuity Equation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
For a two-dimensional steady flow of pore water, any imbalance in flows into and out of an element in the z-direction must be compensated by a corresponding opposite imbalance in the x-direction. Combining the above, and dividing by dx.dy.dz , the continuity equation is expressed as...
Detailed Explanation
This chunk introduces the continuity equation, which represents the conservation of mass in fluid flow. The concept is that if water is flowing steadily, what comes in must balance with what goes out over time. By combining the inflows and outflows on both x and z axes, and dividing by the volume of the element, we arrive at a mathematical representation that can be used for further analysis.
Examples & Analogies
Think of a water balloon. If you squeeze one side, water comes out from the other side. To maintain the balloon's integrity (a steady volume), the amount of water entering from one side must equal what is leaving from the opposite side—this keeps the balloon from bursting.
Integrating Darcy's Law
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
From Darcy's law, where h is the head causing flow. When the continuity equation is combined with Darcy's law, the equation for flow is expressed as...
Detailed Explanation
Darcy's Law describes how fluid moves through porous media, stating that the flow velocity is proportional to the hydraulic gradient, defined by head differences. By incorporating this with the continuity equation discussed prior, we create an equation that precisely models flow through soils. This integrated approach allows engineers and scientists to predict how water will behave in different soil types, especially in engineering and environmental applications.
Examples & Analogies
Imagine riding a bike down a hill (head) where the steepness of the hill dictates how fast you go (flow). In a soil context, Darcy's Law helps illustrate how steep the head (or water pressure) needs to be to push water through the soil at a certain speed.
Flow in Isotropic Materials
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
For an isotropic material in which the permeability is the same in all directions (i.e. k = k ), the flow equation is...
Detailed Explanation
This chunk discusses isotropic materials, meaning that the material's properties are uniform in all directions, affecting how water flows through it. Here, the permeability constant (k) is the same, which simplifies the flow equations. This concept is important for various practical applications, as many soils exhibit isotropic behavior, allowing for easier calculations.
Examples & Analogies
Consider a perfectly round sponge that can absorb water equally from all sides—a property of isotropy. Regardless of how you pour water onto it, it will soak up the same amount at all sides due to its uniform structure.
The Laplace Equation in Three Dimensions
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
For the more general situation involving three-dimensional steady flow, Laplace equation becomes...
Detailed Explanation
Here, the discussion extends to three-dimensional flow scenarios, leading us to the Laplace equation that governs such flows. This equation serves as a fundamental principle in fluid mechanics, particularly in helping solve problems related to groundwater flow in more complex environments, which can have varying soil properties in different directions.
Examples & Analogies
Imagine a large, complex landscape with hills and valleys (three-dimensional). The way water flows through this terrain is influenced by its shape, akin to how Laplace's equation helps us understand and predict water movement in various soil structures, much like mapping river flows in a landscape.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Permeability: A measure of how easily fluid can move through soil, determined by the soil's properties.
-
Darcy's Law: Fundamental principle governing the flow of fluids through porous media.
-
Continuity Equation: Represents mass balance, helping in the analysis of flow in confined spaces.
-
Laplace Equation: Used to model fluid movement, especially in complex and varying soil conditions.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
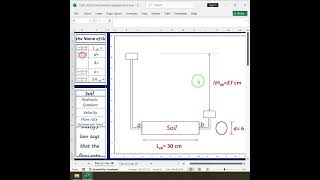
For coarse-grained soil, a constant head test shows consistent water flow indicating high permeability.
-
Using a falling head test on fine-grained soil reveals variable flow rates as the water head decreases over time.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
In soil so fine, water creeps slow, through sandy grains where rivers flow.
📖 Fascinating Stories
-
Imagine a race between water and soil grains – the grains dodge and weave as the water flows swiftly through the wide gaps of sand but struggles to push through the tightly packed clay.
🧠 Other Memory Gems
-
Darcy's Law: Flow = k * (dh/dL); Remember: k means 'King of Permeability!'
🎯 Super Acronyms
PEACE - Permeability Equals Area, Coefficient, Entering flow.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Darcy's Law
Definition:
A law that states the flow rate through a porous medium is proportional to the hydraulic gradient.
-
Term: Continuity Equation
Definition:
An equation that describes the balance of mass, stating that mass entering a system must equal mass leaving the system.
-
Term: Permeability
Definition:
The ability of a material, usually soil, to transmit water or other fluids.
-
Term: Hydraulic Gradient
Definition:
The change in hydraulic head per unit distance; a measure of how much pressure drives the flow.
-
Term: Laplace Equation
Definition:
A second-order partial differential equation that describes the flow of fluids in a steady state.