Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Constant Head Permeameter
Unlock Audio Lesson
Today we're diving into the concept of constant head flow. Can anyone tell me what a constant head permeameter is?
Is it a device used to measure the permeability of coarse-grained soils?
Exactly! It measures how fast water can flow through coarse soils by keeping the water head constant. Why is this method not suitable for fine-grained soils?
Because the flow rate is variable and harder to measure in fine soils?
Correct! And remember, we can calculate permeability (k) using the head drop (h) over a specific distance (L). A mnemonic to recall this could be 'Keep Heads Low' for 'k = h/L'.
So, what does that formula represent in real-world applications?
Great question! It helps predict how quickly groundwater can flow through different soils, crucial for construction and environmental assessments.
To recap, we learned that the constant head permeameter is vital for coarse-grained soils and helps us calculate flow rates efficiently.
Falling Head Permeameter
Unlock Audio Lesson
Now, let’s discuss the falling head permeameter. What do you think it measures?
It measures permeability for fine-grained soils, right?
That's right! In this setup, the head (h) falls as time progresses. Why do you think this method is necessary for fine-grained soils?
Because the fine sediments have small pores that require measuring the change in head over time?
Yes! We need to track how the hydraulic gradient changes, which can be described mathematically. Can you think of any challenges posed by this method?
It seems like it would be more complex than the constant head method, right?
Exactly! The calculations involve a relationship between head drops at different times. A helpful mnemonic is 'Failing Heads Change' for 'Falling Head Changes'.
To summarize, the falling head permeameter is effective for measuring fine-grained soil permeability by analyzing head decline over time.
Darcy's Law and Continuity Equation
Unlock Audio Lesson
Let’s shift gears to Darcy's Law. Who wants to explain what it states?
Darcy's Law describes the flow of fluid through porous media, right?
Correct! It’s fundamentally important for both methods we talked about. Can anyone summarize how we combine Darcy's law with the continuity equation?
I think we express flow continuity to ensure inflow and outflow balance in soil!
Exactly! That's how we derive the Laplace equation for flow. How does that help us in practical terms?
By providing a mathematical model to predict groundwater flow?
Yes! So remember, the continuity equation ensures balance in mass flow, which is essential for further calculations. Let's keep in mind 'Daring Quickly' to link Darcy and continuity!
In summary, Darcy's Law integrates with the continuity equation to form essential flow equations for predicting soil behavior.
Application of Flow Equations
Unlock Audio Lesson
Today we’ll see how these theories apply practically. Can someone give me an example of where understanding soil permeability is crucial?
In construction projects, like determining the best spot for a building's foundation!
Great example! Permeability influences how water drains and affects the integrity of structures. How else might these equations be useful?
They could also be necessary for environmental assessments, like predicting contamination spread.
Exactly! Understanding the flow of water through soils helps manage resources sustainably and avoids disasters. A useful acronym here is 'SAFE' - 'Soil Assessments for Future Engineering'.
To recap, soil permeability and flow equations are crucial tools for engineers and environmentalists in addressing both construction and ecological challenges.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
This section defines the constant head permeameter for coarse-grained soils, detailing how it measures permeability via steady water flow and head drop. It contrasts this with the falling head permeameter used for fine-grained soils, explaining the relationship between head drop and permeability through mathematical equations.
Detailed
Constant Head Flow
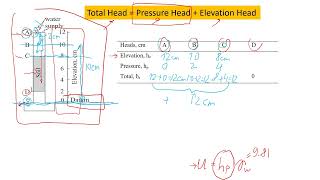
The Constant Head Flow method involves measuring the permeability of soils using a constant head permeameter, which is mainly suitable for coarse-grained soils. In this setup, water flows through a soil sample of cross-sectional area (A) while measuring the total head drop (h) across the length (L) of the sample. The rate of flow is consistent and allows for precise measurements of permeability (k).
Conversely, the Falling Head Flow method is more suited for fine-grained soils where the total head (h) in a standpipe decreases over time. This setup allows us to measure the hydraulic gradient at different intervals, which complicates calculations but is necessary for finer materials.
A mathematical expression derives the permeability from both methods, incorporating Darcy's Law which describes the flow of water through a soil element. This combination leads to the formulation of continuity equations and the Laplace equation, essential for understanding two-dimensional and three-dimensional steady state flows.
Understanding these relationships is critical for assessing soil behavior during engineering projects and in environmental settings.
Youtube Videos
![Geotechnical Eng'g 1 (Soil Mechanics) - Permeability of Soil (Part 1) [Sample Problems]](https://img.youtube.com/vi/HU1QMx4htFU/mqdefault.jpg)
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Constant Head Permeameter
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Constant head permeameter is recommended for coarse-grained soils only since for such soils, flow rate is measurable with adequate precision.
Detailed Explanation
A constant head permeameter is an instrument used to measure the permeability of soil, specifically suitable for coarse-grained soils like sand and gravel. This method allows for a steady flow of water through the soil sample, meaning the flow rate can be accurately measured. The term 'constant head' means that the water level is maintained at a fixed height during the test, which provides consistent pressure and thus, reliable results.
Examples & Analogies
Imagine watering a garden. If you use a hose with a constant water supply (constant head) at the same pressure, you can easily predict how quickly the water will seep into the soil. However, if the soil were very fine (like clay), it would not drain properly, leading to inconsistent measurements of how fast the water flows through. So, we use constant head testing primarily for the more coarse soils.
Measuring Flow and Head Drop
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
As water flows through a sample of cross-section area A, steady total head drop h is measured across length L.
Detailed Explanation
During a constant head flow test, water is allowed to flow through a soil sample of known cross-sectional area (A). The total head drop (h), which is the difference in water levels measured over a specific length (L) of the soil sample, is observed. This head drop is critical because it influences the speed at which water can move through the soil, thereby helping to determine the soil's permeability.
Examples & Analogies
Think of a slide at a playground. The height of the slide at the start (head) affects how fast a child can go down. Similarly, the head drop during the water flow test determines how quickly water moves through the soil sample.
Calculating Permeability
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Permeability k is obtained from:
Detailed Explanation
The permeability (k) is a measure of how easily water can flow through the soil. It is calculated using the measurements taken during the test. The formula for calculating permeability generally involves the cross-sectional area of the soil sample, the head difference, and the length of the sample. This allows engineers to understand the drainage and flow characteristics of the soil for construction projects.
Examples & Analogies
Consider a sponge. If you press it lightly, water seeps out slowly (low permeability). If you press harder, more water flows out quickly (high permeability). The formula for k helps us predict how 'sponge-like' different soils will behave when water is applied.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Constant Head Permeameter: Measures permeability for coarse-grained soils using a steady water flow.
-
Falling Head Permeameter: Measures permeability for fine-grained soils over time as the water head decreases.
-
Darcy's Law: Governs fluid flow through soil's pore spaces, essential in defining permeabilities.
-
Continuity Equation: Ensures balance between flow in and out of soil elements.
-
Laplace Equation: Governing equation derived for predicting steady-state flow in soils.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Using a constant head permeameter on sand to measure how quickly water passes through at a given height.
-
Using a falling head permeameter on clay to observe how head drop changes over a specified time period.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
In soils coarse, flow is force, with constant head we chart the course.
📖 Fascinating Stories
-
Imagine a water park where water flows through sand, steady and fast; but when it hits clay, it slows down, and oh, what a splash!
🧠 Other Memory Gems
-
Remember 'DHC' for Darcy's law - Head pressure Controlled flow.
🎯 Super Acronyms
PEACE stands for Permeability Equations Affect Coarse and fine soils.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Permeability (k)
Definition:
The ability of soil to transmit water, typically expressed in terms of flow rate per unit area and hydraulic gradient.
-
Term: Constant Head Permeability Test
Definition:
A laboratory method for measuring the permeability of coarse-grained soils under a constant hydraulic head.
-
Term: Falling Head Permeability Test
Definition:
A laboratory method used for measuring permeability in fine-grained soils where the hydraulic head falls over time.
-
Term: Darcy's Law
Definition:
A fundamental equation that relates the flow of fluid through porous media to the hydraulic gradient and material properties.
-
Term: Continuity Equation
Definition:
A mathematical expression that ensures the balance of inflow and outflow in a flow system.
-
Term: Laplace Equation
Definition:
An equation derived from the continuity equation and Darcy's law, governing flow in saturated soils.