Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to the Case Study
Unlock Audio Lesson
Today, we're going to look at a real-world case study involving rainfall data. Have any of you heard of how rainfall measurements can become inconsistent?
I think it can happen due to changes in the environment around the gauge.
Exactly! In this case study, we have a rain gauge at Station A showing a sudden increase in rainfall after 1990. Why do you think that's critical?
Because it might affect the conclusions about hydrological studies?
Correct! Inconsistent data can lead to poor decisions in water resource management. Let's see how we analyze this situation.
Analyzing the Data
Unlock Audio Lesson
To assess the consistency of the rainfall data from Station A, we use the Double Mass Curve method. What do you think is the first step?
We need to collect cumulative rainfall data from Station A and nearby stations.
Good! We then plot this data. Can anyone tell me what a straight line on this graph would indicate?
It means the data is consistent, right?
Correct! A change in slope shows inconsistency. What do we do next?
Correction of Data
Unlock Audio Lesson
After plotting the Double Mass Curve, we identified a significant deviation around 1990. What is our next step?
We need to figure out the correction factor.
Absolutely! We calculate the slope ratio before and after the deviation. Who can remind us why this step is necessary?
It's to adjust the rainfall values to restore consistency!
Exactly. Adjusting ensures that the data can be used reliably in hydrological models. This step is crucial.
Final Adjustments
Unlock Audio Lesson
After calculating our correction factor, what do we do with the rainfall data from 1990 onwards?
We apply the correction factor to those values.
Correct! This adjustment helps restore consistency and enables us to use the data for future hydrological modeling effectively. Why is that important?
So we can make better decisions in engineering and water management!
Absolutely! The integrity of data is key in both urban planning and environmental studies.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
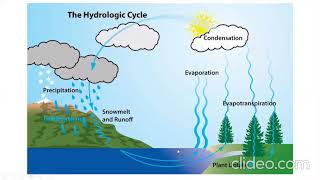
The section presents an illustrative case study involving a rain gauge at Station A, which indicated a significant increase in rainfall after 1990. It describes the procedures followed for checking data consistency using the Double Mass Curve method and illustrates how adjustments were made to ensure the data can be confidently used for hydrological modeling.
Detailed
Detailed Summary
In this section, we explore a case study featuring a rain gauge at Station A, which exhibits a sudden increase in recorded rainfall post-1990 compared to prior years and neighboring stations. This anomaly raises concerns about data consistency, which is vital for accurate hydrologic studies and infrastructure design.
Key Steps for Data Assessment
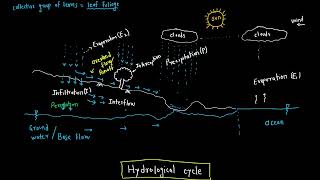
- Double Mass Curve Analysis: The initial step involves plotting a Double Mass Curve using cumulative rainfall data from Station A alongside neighboring stations. This linear plot helps visualize rainfall consistency.
- Identification of Deviation: The graph analysis reveals a deviation or change in slope around 1990, indicating a shift in recording conditions.
- Correction Factor Calculation: The next step is calculating the correction factor by determining the slope before and after 1990. This ratio informs how the inconsistent data should be adjusted.
- Data Adjustment: Lastly, the rainfall values from 1990 onward are adjusted using the computed correction factor. This adjustment restores data consistency, making it suitable for hydrological modeling tasks.
This case study underscores the importance of applying statistical methods for ensuring the reliability of hydrological data, emphasizing the critical role of consistent rainfall records in engineering and environmental management.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to the Case Study
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Suppose a rain gauge at Station A shows a sudden increase in rainfall after 1990, compared to its past trend and neighboring stations.
Detailed Explanation
This introduction establishes the context for the case study. Station A has reported a new trend where rainfall appears to dramatically increase starting in 1990. This observation is critical because it might indicate a problem with the data rather than an actual change in rainfall patterns. It sets the stage for the following steps, which are methods to investigate this anomaly.
Examples & Analogies
Imagine measuring your height over time. If you suddenly appear to have grown significantly taller at a certain age, it might prompt you to check if the measuring tape was accurate or if you stood differently. Just like that, inconsistencies in rainfall data need to be examined to ensure they reflect true changes.
Plotting the Double Mass Curve
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Steps:
1. Plot Double Mass Curve with cumulative data.
Detailed Explanation
The first action in resolving this inconsistency is to create a Double Mass Curve (DMC). This visual tool compares the cumulative rainfall of Station A against the cumulative rainfall of neighboring stations. The DMC plots the total amount of rain over time for both Station A and the neighbors, allowing for easy identification of discrepancies in recorded data.
Examples & Analogies
Think of the Double Mass Curve like a balance scale. If one side (Station A) suddenly starts piling on more weight (rainfall) compared to the other sides (neighboring stations), it indicates that something is off-balance, suggesting you need to investigate.
Identifying the Point of Deviation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
- Identify the point of deviation around 1990.
Detailed Explanation
After plotting the DMC, the next step is to look for any points where the trend diverges. In this case, the point around 1990 is highlighted because it marks a change in the data pattern. This is crucial as it pays particular attention to identification of the exact time when the inconsistency began, enabling further analysis of what may have caused the discrepancy.
Examples & Analogies
Imagine watching a movie where the plot suddenly changes direction. If the characters act differently starting from a specific scene, you'll want to pinpoint that scene to understand what happened. Similarly, in data analysis, identifying when changes occur is important.
Computing the Correction Factor
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
- Compute the correction factor using slope ratio before and after 1990.
Detailed Explanation
Once the point of deviation is identified, the next step is to calculate a correction factor. This involves determining the slope ratio of the cumulative rainfall data before and after the identified year (1990 in this case). The slope ratio helps in quantifying how much the rainfall data from Station A diverges from what would be expected based on the neighboring stations' data, allowing for appropriate adjustments.
Examples & Analogies
Suppose you realize your car has been using more fuel after an engine modification. To correct this, you figure out how much fuel it used to consume compared to its current consumption. By calculating the difference, you can adjust your driving to optimize fuel efficiency, just like adjusting for errors in data.
Adjusting Values for Consistency
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
- Adjust values of Station A from 1990 onwards using the correction factor.
Detailed Explanation
The final step is to apply the computed correction factor to the rainfall records of Station A from the year 1990 onward. This adjustment is intended to align Station A's data with the trends observed in the neighboring stations, effectively restoring consistency to the records and making them suitable for hydrological modeling.
Examples & Analogies
Think of this adjustment like fixing a mistake in your final exam paper. If you realize you added an extra answer that wasn't supposed to be there, once you remove it or correct it, your overall score reflects your true performance more accurately, just like how adjusted rainfall data will more accurately represent actual conditions.
Outcome of Adjustments
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
This adjustment restores the consistency and makes the data usable for hydrological modeling.
Detailed Explanation
After all adjustments are made, the data is once again considered reliable and suitable for use in hydrological studies and modeling. This means that engineers and planners can confidently use the revised data to design infrastructure, forecast floods, and manage water resources without the risk of inaccuracies stemming from previous inconsistencies.
Examples & Analogies
Just as a renewed and corrected financial report can help a business make sound investments, rectifying discrepancies in rainfall data allows engineers to make informed decisions about water management and infrastructure design.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Consistency in Rainfall Data: Refers to the reliability of rainfall measurements critical for hydrological studies.
-
Double Mass Curve: A tool used to identify inconsistencies in rainfall data through cumulative comparison.
-
Correction Factor: A calculated value applied to adjust inconsistent data to restore reliability.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
The case of Station A where the rainfall increased after 1990, causing concerns regarding the reliability of the data, demonstrates the impact of environmental changes on rainfall measurements.
-
Using the Double Mass Curve, we were able to visually identify the year where data inconsistency began and apply necessary corrections.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
In rainfall plots where the line is straight, data is consistent and truly great.
📖 Fascinating Stories
-
Once there was a rain gauge in Station A that saw a strange increase post-1990. The engineers gathered and plotted its data, only to find slopes that spoke of wild shifts brewing. They applied their clever correction factor, restoring the gauge to reliable status for the city's water tales!
🧠 Other Memory Gems
-
Remember the acronym DMC: Data (Double) Mass Curve, used for checking rainfall consistency!
🎯 Super Acronyms
C.A.R.E for rainfall consistency
- Collect data
- Analyze it
- Restore it
- and Ensure reliability.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Double Mass Curve
Definition:
A graphical technique used to assess the consistency of rainfall data by plotting cumulative values from one station against another.
-
Term: Correction Factor
Definition:
A ratio used to adjust rainfall values to account for inconsistencies identified in hydrological data.
-
Term: Consistency in Rainfall Data
Definition:
Reliability of rainfall records over time, crucial for effective hydrological modeling and water resource management.