Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Consistency Checks
Unlock Audio Lesson
Today, we will be discussing the importance of checking the consistency of rainfall data before we estimate any missing values. Why do you think this step is crucial?
Maybe to ensure that our estimates are accurate?
Exactly! If our data isn't consistent, our estimations will be unreliable. We primarily use the Double Mass Curve method for this. Can anyone tell me what that is?
Is it something to do with plotting rainfall data?
Yes, right! We plot cumulative rainfall from our station against neighboring stations. What do you think the outcome tells us?
If it's a straight line, the data is consistent?
Correct! But if there’s a slope break, that indicates there’s something wrong. We might need to adjust that section. Let's summarize: before estimating data, verify consistency!
Double Mass Curve Method Procedure
Unlock Audio Lesson
Let's go into detail about the Double Mass Curve method. First, what should we plot?
We plot the cumulative rainfall of our station with the mean of nearby stations.
Exactly! Once we do that, how do we determine if our data is good?
If the plot is linear, that means our data is consistent.
Right! And what happens if there's a break in slope?
It suggests inconsistency, and we might need to adjust our readings.
Precisely! Summarizing, linear plots confirm consistency, while breaks indicate the need for adjustments. Remember this when working with real data!
Practical Applications of Consistency Checks
Unlock Audio Lesson
Now that we know how to check consistency, can anyone suggest why this might be important in practice?
It could help improve our water resource management.
Absolutely! Accurate rainfall data is essential for designing dams and flood control projects. What can happen if we don’t verify our data?
We could make wrong estimations, right?
Exactly! Errors may lead to costly mistakes in project designs. Consistency checks help ensure everything is reliable.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In this section, the focus is on the critical process of checking the consistency of rainfall records. Utilizing the Double Mass Curve technique, students learn how to identify consistency in cumulative rainfall data, adjust for inconsistencies, and ensure reliable rainfall estimations.
Detailed
Checking the Consistency of Rainfall Data
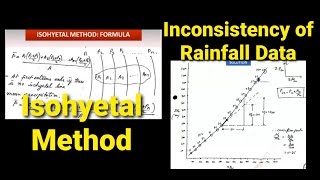
Before attempting to estimate any missing rainfall data, it is essential to first verify the consistency of the available records to ensure reliable results. The Double Mass Curve Method serves as a powerful tool in this verification process.
Procedure of Double Mass Curve Method
- Plot Cumulative Rainfall: Start by plotting the cumulative rainfall amounts of the station under consideration against the cumulative mean of nearby stations.
- Analyze the Plot:
- If the resulting plot is linear, this points to a consistency in the data.
- If there is a break in the slope, it indicates inconsistencies which could be due to various factors, such as changes in gauge location or instrument malfunction.
- Adjustment of Data: In cases of detected inconsistencies, it becomes necessary to adjust the problematic portion using correction factors derived from the changes in slope.
Understanding this method is crucial, as inconsistencies can lead to errors in hydrological analysis and project designs that depend heavily on accurate rainfall estimations.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Purpose of Checking Consistency
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Before estimating missing data, it is crucial to verify the consistency of the available records.
Detailed Explanation
Consistency checks are essential because they ensure that the data we have is reliable and can be used to make accurate estimates. If the data has inconsistencies, any estimations made will also be unreliable. Therefore, checking how consistent the rainfall data is before proceeding with further analysis is a critical step in the data correction process.
Examples & Analogies
Imagine a teacher trying to calculate the average score of a class based on students' test scores. If some scores are missing or if there are grades that don't make sense (like a score of 150 out of 100), the teacher will not get an accurate average. Similarly, verifying the consistency of rainfall data ensures that the calculations made afterward reflect the true situation.
Double Mass Curve Method
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
This is commonly done using a Double Mass Curve.
Detailed Explanation
The Double Mass Curve method involves plotting the cumulative rainfall of the station being studied against the cumulative mean of nearby stations. This visual representation helps to easily spot whether the data follows a consistent pattern. A linear plot indicates that the data is consistent, whereas any breaks or changes in slope can suggest issues with the data, indicating possible inconsistencies or changes in measurement conditions.
Examples & Analogies
Think of the Double Mass Curve like drawing a line on a map where friends have taken turns walking on a path. If everyone walks in a straight line, you can easily see where they’ve gone. If someone suddenly veers off into the woods or starts going backward, that break in the path signals something went wrong, similar to how inconsistencies in rainfall data reveal potential problems.
Interpreting the Plot
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
If the plot is linear → data is consistent. If there’s a break in slope → indicates inconsistency or change in gauge location/instrument.
Detailed Explanation
When analyzing the plot from the Double Mass Curve, a linear relationship means that the rain gauge is functioning well and the data is trustworthy. However, if the line shows a break or a slope change, it either means there’s been a significant change in rainfall patterns or a problem with the equipment. Understanding this is key to decide if you can use the data directly or if it needs to be adjusted first.
Examples & Analogies
Imagine reading a story that generally follows a clear plot but suddenly switches to a different storyline or has missing pages. Just like in the confusing story, a break in the rainfall data can lead to misinterpretations. So, identifying breaks in the Double Mass Curve is like recognizing a shift in a narrative that may change how we understand the entire story.
Correction of Inconsistent Data
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Correction: Adjust the inconsistent portion using correction factors derived from the slope changes.
Detailed Explanation
When a break in slope is identified, it’s crucial to correct those portions of the data to maintain accuracy. Correction factors, which are derived from analyzing how much the slope changed, allow for adjustments to be made to the recorded data, making it more reliable for subsequent analysis or estimation.
Examples & Analogies
Consider a puzzle where some pieces don't fit quite right. By identifying which pieces (or data points) are inconsistent and understanding how they should fit into the overall picture, you can adjust them to create a proper, complete image of the rainfall data, much like doing corrections on a flawed mathematical solution to achieve the correct answer.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Double Mass Curve: A method of verifying the consistency of rainfall data.
-
Cumulative Rainfall: Important for understanding how much rainfall has accumulated over time.
-
Slope Break: An indication of inconsistencies that may require correction.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
If the cumulative rainfall for station A is plotted against the mean cumulative rainfall of three neighboring stations and shows a linear relationship, it indicates that station A’s data is consistent.
-
A slope break observed in the plot suggests the need to investigate gauge malfunction or location changes affecting rainfall readings.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
If the line is straight, it's true, data reliable too.
📖 Fascinating Stories
-
Imagine a detective analyzing rainfall—a smooth plot means a clear case, but a break signals something amiss that needs solving.
🧠 Other Memory Gems
-
Remember C-C-S: Consistency means Cumulative data is Consistent and Straight.
🎯 Super Acronyms
DMC - Double Mass Curve for Data consistency verification.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Double Mass Curve
Definition:
A method used to analyze the consistency of rainfall data by plotting cumulative rainfall of one station against the cumulative mean of nearby stations.
-
Term: Cumulative Rainfall
Definition:
The total amount of rainfall accumulated over a defined period.
-
Term: Slope Break
Definition:
A change in the trend of a plotted graph indicating potential inconsistencies in data.