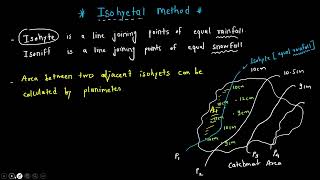
9.2. Isohyetal Method

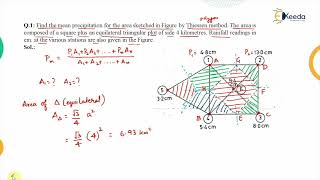
The Isohyetal Method is a contouring technique used to estimate areal precipitation. It involves drawing isohyets, which are lines connecting points of equal rainfall depth, based on measurements from different stations. This method is considered more accurate than Theissen’s because it incorporates spatial rainfall gradients and allows interpolation between stations.

The Isohyetal Method works by using contour lines, known as isohyets, to visually represent rainfall data. These lines connect points that receive the same amount of rainfall, allowing for a more comprehensive view of how precipitation varies over an area. Unlike the Theissen Polygon Method that simplifies rainfall distribution, the Isohyetal Method acknowledges the gradual changes in rainfall intensity, making it more reliable especially in areas with varying topography.

Imagine you're looking at a topographic map of a mountain range. Just as contour lines indicate elevation, isohyets show how rainfall changes across the landscape. If one part of the mountain gets 10 inches of rain while another gets 5 inches, the isohyets will help represent this difference clearly, allowing for better planning and resource management.

1. Plot the catchment boundary and mark all rain gauge stations with recorded rainfall values.
2. Interpolate rainfall between nearby stations and draw isohyets (contour lines of equal rainfall).
3. Divide the catchment into zones between isohyets.
4. Measure the area between each pair of isohyets.
5. Assign the average precipitation to each zone, calculated as the mean of the two bounding isohyets.
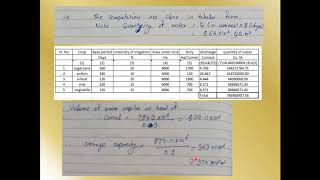
6. Compute the area-weighted average rainfall as: n (cid:18) (cid:19) P = X A i × P avg A i total i=1 • where: – A = area between two isohyets i – P = average rainfall between two isohyets i

To effectively apply the Isohyetal Method, follow these steps: First, draw the boundary of the area you're studying and mark the locations of all rain gauges that have recorded precipitation. Next, use the data from these stations to estimate rainfall amounts in between them, and sketch the corresponding isohyets. The area between these lines are then divided into different zones. You'll calculate the average rainfall for each zone based on the heights of the isohyets on either side of it. Finally, you compute the area-weighted average rainfall for the entire catchment area.

Think of the catchment area like a large sheet of land where each rain gauge is a point of reference, much like stars in the sky. Just as astronomers connect stars to create constellations, hydrologists connect rainfall data points to create isohyets, which paint a picture of how precipitation is distributed across the area. This allows planners to understand which parts get more rain and which get less, similar to knowing which spaces in a garden get more sun or shade.

• Use interpolation between stations to place isohyets accurately. • Rainfall contours must follow logical patterns (e.g., they should not cross unless justified by topography). • The denser the station network, the more reliable the isohyets.

When drawing isohyets, it's important to interpolate—the process of estimating values between two known values. This ensures that the flow of rainfall data remains logical. Isohyets should not cross as this would indicate illogical rainfall distribution unless justified by distinct topographical changes like mountains or valleys. Furthermore, a higher number of rain gauges increases reliance on your contours as it provides a more detailed dataset to draw from.

Imagine painting a landscape where you want to show how the light changes as you move from one side of a hill to the other. Using too few colors would yield a simplistic and potentially inaccurate representation. But if you use many shades and gradients, your painting will reflect the many variations more realistically. Similarly, having more rain gauges will give a clearer picture of how rainfall changes across the landscape.

• Most accurate among the non-instrumental methods for estimating areal rainfall. • Considers spatial variations and gradients of rainfall. • Can reflect topographic influences when isohyets are drawn carefully.

The Isohyetal Method is praised for its accuracy because it factors in how rainfall amounts can shift significantly due to geographical features. It provides a rich depiction of variability, as opposed to relying on average rainfall across a broad area. When performed carefully, the method also reflects changes in elevation and terrain, making it particularly useful in regions where these elements influence precipitation patterns.

It's like using a detailed map of a city versus a basic outline—while a simple map might show you where the streets are, the detailed version would tell you where the hills are, where it might flood, or where traffic might be heavier. The Isohyetal Method does something similar for rainfall, ensuring that planners know where to allocate resources and prepare for water management.

• Time-consuming and requires experience. • Subjective element in drawing isohyets—results may vary with person. • Needs a dense network of rain gauge stations for better accuracy.

While the Isohyetal Method is valuable, it does come with drawbacks. It can take a significant amount of time to complete since you have to carefully interpolate and draw the contours. Additionally, because it involves some artistic judgment in drawing isohyets, different hydrologists might produce slightly varied results based on personal interpretation. Furthermore, to achieve the best results, a close network of rain gauges is essential, or else the contours may not accurately depict actual conditions.

Consider it like baking a complex recipe. If you don’t follow the steps precisely or if you miss an ingredient, you may not end up with the right flavor. Similarly, if a hydrologist does not accurately create the isohyet map or if there are not enough sampling stations, the results could be significantly off, leading to potential mismanagement of water resources.

--