Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Theissen Polygon Method
Unlock Audio Lesson
Welcome, everyone. Today, we will discuss the Theissen Polygon Method. Can anyone tell me what this method is primarily used for in hydrology?
Is it used to calculate average rainfall over a larger area by using data from specific rain gauge stations?
Exactly! The Theissen Polygon Method estimates area-weighted average rainfall based on point observations from different stations. Now, why do we need to interpolate this data instead of using just the measurements directly?
Because rainfall can vary across different areas, and we want a complete picture of what’s happening in the whole catchment.
Right! We want to understand how rainfall varies spatially over the catchment area.
Constructing Theissen Polygons
Unlock Audio Lesson
Let's talk about how to construct the Theissen polygons. The first step involves plotting the catchment area on a map and locating all the rain gauges. What do you think is the next step?
Connecting the stations with lines to form triangles, right?
Exactly! After that, we draw the perpendicular bisectors to form polygons. Can anyone remember how we calculate the average rainfall once we have the polygons?
By multiplying the area of each polygon by the rainfall measured at the respective station and then dividing by the total area!
That's correct! It's a simple calculation yet crucially important.
Assumptions and Limits of the Method
Unlock Audio Lesson
Now, let's consider the assumptions of the Theissen Polygon Method. One key assumption is that rainfall is uniformly distributed within each polygon. Why might this be a concern?
Because in reality, rainfall can be affected by many factors like elevation and local weather patterns.
Precisely! Also, we assume that the catchment area is adequately covered with rain gauges. What problems could arise from that?
If there are too few gauges, we might miss important data or make inaccurate estimates.
Excellent point! Accurate distribution of stations is vital for reliable results.
Merits and Demerits
Unlock Audio Lesson
Let's discuss the merits and demerits of using the Theissen Method. Can anyone share one merit?
It’s simple and easy to apply, making it great for quick estimates.
Absolutely! And on the flip side, what’s a significant drawback?
It ignores factors like elevation, which can greatly affect rainfall distribution.
Very true. Understanding both the strengths and weaknesses helps us apply the right methods in hydrology.
Applications of Theissen Polygon Method
Unlock Audio Lesson
Let’s conclude by discussing when to use the Theissen Polygon Method. In which scenarios do you think this method would be beneficial?
It’s helpful in small watersheds where we need quick rainfall estimates.
Exactly! It’s also beneficial when we have limited resources for more complex analyses. Why wouldn’t we use it for larger basins?
Because larger basins have more varied topography and rainfall patterns that this method can’t account for.
Great insights! Understanding these applications helps us choose the appropriate method for our hydrological challenges.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
This method creates polygons around rain gauge locations, assigning precipitation based on these polygons' area to estimate average rainfall across a catchment. While simple and effective for small to medium-sized areas, the method has limitations in terms of topography and station distribution.
Detailed
Theissen Polygon Method
The Theissen Polygon Method, also known as the Thiessen Method, is a prevalent geometrical approach used in hydrology for estimating area-weighted average rainfall based on point observations from rain gauge stations. The core assumption is that each rain gauge influences a specific area within a catchment, delineated by polygons constructed around each station.
Steps of Construction
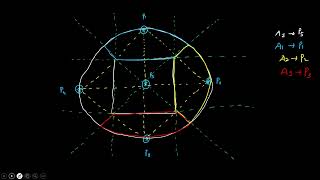
- Mapping Stations: First, the catchment area is plotted on a map, marking all rain gauge stations.
- Triangulation: Adjacent stations are connected to form triangles.
- Perpendicular Bisectors: The perpendicular bisectors of each line connecting two adjacent stations are drawn.
- Creating Polygons: The intersection of these bisectors creates polygons, defining the area of influence for each station.
- Area Measurement: The area of each polygon is then measured using appropriate tools.
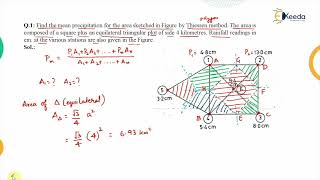
- Rainfall Calculation: The area-weighted average rainfall is computed using the formula:
$$P_{avg} = \frac{\sum_{i=1}^{n} (A_i \times P_i)}{A_{total}}$$
where $A_i$ is the area of the ith polygon, $A_{total}$ is the total catchment area, and $P_i$ is the precipitation at the ith station.
Assumptions
- Uniform rainfall distribution within each polygon.
- No consideration of orographic or topographical influences.
- Adequate coverage of the catchment area by rain gauges.
Merits
- Easy to implement and comprehend.
- Effective for small to medium catchments.
- Deals with spatial variability better than the arithmetic mean method.
Demerits
- Overlooks elevation and topographic features.
- Relies on an appropriate distribution of rain gauges for accuracy.
- Unrealistic sharp boundaries in rainfall distribution.
This method, while commonly used, is more suitable for preliminary studies as it does not account for complex hydrological processes found in larger basins.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Concept and Purpose
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The Theissen Polygon Method (also known as the Thiessen Method) is a geometrical approach used to estimate area-weighted average rainfall from point observations at rain gauge stations. It assumes that each station is responsible for rainfall over a specific area, bounded by polygons constructed around the stations.
Detailed Explanation
The Theissen Polygon Method is a method used to calculate average rainfall over a specific area using data collected from various rain gauge stations. The key idea is that each weather station is thought to only influence a particular region surrounding it. This region is represented by a polygon formed by connecting lines between adjacent stations. Therefore, the rainfall recorded at each station is 'responsible' for the area within its polygon.
Examples & Analogies
Imagine a pizza with different slices representing different neighborhoods (each neighborhood has a rain gauge). Just like each slice corresponds to a neighborhood, each polygon corresponds to the area represented by a rain gauge. When you want to know how much rain fell on the entire pizza, you look at the total amount of rainfall in each neighborhood slice.
Steps of Construction
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
- Plot the catchment area on a map and mark the location of all rain gauge stations.
- Connect adjacent stations with straight lines to form triangles (Triangulation).
- Draw perpendicular bisectors of each line connecting two adjacent stations.
- The intersection of perpendicular bisectors creates polygons around each station.
- Each polygon defines the area of influence of that rain gauge.
- Measure the area of each polygon using a planimeter or CAD tools.
- Calculate weighted average rainfall as:
$$ P_{avg} = \frac{\sum_{i=1}^{n} A_i \times P_i}{A_{total}} $$
where:
– $A_i$ = area of the $i^{th}$ polygon
– $A_{total}$ = total catchment area
– $P_i$ = precipitation at the $i^{th}$ station
Detailed Explanation
The construction of Theissen polygons involves several systematic steps: First, one must identify and mark all the rain gauge stations on a map of the catchment area. Next, triangles are formed by connecting stations with straight lines. The next step is to draw perpendicular bisectors for each line, which will ultimately intersect and form the polygon boundaries around each station. Once the polygons are established, the area of each polygon can be calculated, usually with the help of tools like planimeters or computer-aided design software. Finally, the average rainfall is determined by weighting the rainfall amounts by the area of their corresponding polygons for the entire catchment area.
Examples & Analogies
Think of it like dividing a garden into sections based on where you have sprinklers (rain gauges). Each sprinkler has a specific area it waters. By determining how much water each sprinkler (gauge) puts out and its area, you can find out how much water is used efficiently across the entire garden, just as we calculate the average rainfall across a larger area using Theissen polygons.
Assumptions
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
• Rainfall is uniformly distributed within each polygon.
• No orographic or topographic influence is considered.
• The catchment area is adequately covered by rain gauges.
Detailed Explanation
The Theissen Polygon Method relies on several key assumptions to work effectively: It is assumed that within each polygon, rainfall is evenly distributed, meaning that all areas receive the same amount of rain as measured by the gauge. It does not take into account any variations due to changes in elevation (orography) or landscape features (topography), which could otherwise impact rainfall distribution. Lastly, it is assumed that there are enough gauges situated throughout the catchment area to adequately represent the rainfall effectively.
Examples & Analogies
Imagine you're having a barbecue in your backyard, and you have rain gauges placed across the lawn. If you assume each gauge collects the same amount of rain as the others, you might not notice that one side of the lawn is on a slope and therefore gets more rain. This method oversimplifies the reality, just like the assumptions made in the Theissen method.
Merits
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
• Simple and easy to apply.
• Useful for small to medium-sized catchments.
• Accounts for spatial variability better than the arithmetic mean method.
Detailed Explanation
The Theissen Polygon Method has several advantages. Firstly, it is straightforward and does not require complex calculations, making it user-friendly. It is particularly beneficial for small to medium catchments where rainfall can be effectively approximated with this method. Additionally, it considers the distribution of gauges and the areas they cover, leading to a more accurate representation compared to simply averaging values from the gauges (arithmetic mean), which may overlook spatial differences.
Examples & Analogies
If you think of how restaurants assess average customer satisfaction, the Theissen method is like gathering feedback from diners based on the size of the table they occupied rather than just taking a quick overall survey across the entire restaurant without any specific focus. This ensures you're getting a more reliable understanding of which areas are succeeding or failing.
Demerits
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
• Ignores elevation and topographical features.
• Accuracy depends on the proper distribution of stations.
• Sharp boundaries are unrealistic in natural rainfall distribution.
Detailed Explanation
Despite its merits, the Theissen Polygon Method has limitations. It does not account for differences in elevation or landform, which can significantly affect rainfall patterns. The accuracy of the method is reliant on how well the rain gauges are positioned; if they are not well-distributed, the resulting estimates can be flawed. Additionally, the method creates sharp polygon boundaries which can be illogical, as rainfall does not usually have such abrupt transitions in real environments.
Examples & Analogies
It's like planning a party around neighborhoods but ignoring the fact that some areas have hills while others are flat – if you only look at community borders without considering the landscape, your party might miss key locations with friends who could show up!
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Geometry in Hydrology: The use of geometrical methods to represent rainfall data spatially.
-
Construction Steps: Detailed steps for creating Theissen polygons from rain gauge data.
-
Assumptions: The underlying assumptions that impact the accuracy and applicability of the method.
-
Advantages and Disadvantages: The strengths and weaknesses of the Theissen Polygon Method in rainfall estimation.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Using the Theissen Polygon Method, an area with three rain gauges can be analyzed to determine which gauge's rainfall significantly influences adjacent areas through structure-defined polygons.
-
In a small watershed with evenly distributed rain gauges, the method can provide quick and reliable rainfall estimates for preliminary assessments.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Polygons we divide, rainfall we derive; Theissen’s savvy way, keeps errors at bay.
📖 Fascinating Stories
-
Imagine a rain gauge in the center of a star. Each ray represents a polygon where that gauge’s rainfall is paramount.
🧠 Other Memory Gems
-
P.A.W.S: Plot, Adjacent lines, Wield bisectors, Sum areas.
🎯 Super Acronyms
R.A.P
- Rain estimate
- Area influence
- Polygon construction.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Theissen Polygon Method
Definition:
A geometrical method to estimate area-weighted average rainfall based on point observations from rain gauge stations.
-
Term: Rain Gauge
Definition:
A device used to measure the amount of liquid precipitation over a set period.
-
Term: AreaWeighted Average Rainfall
Definition:
An average precipitation value for an entire area, calculated by weighting individual measurements by the area they influence.
-
Term: Triangulation
Definition:
The process of dividing an area into triangles for the purpose of obtaining a geometric representation of various locations.
-
Term: Perpendicular Bisectors
Definition:
Lines that bisect the segment joining two points at a right angle, used to create boundaries for polygons.