Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Darcy’s Law
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Today, we're going to discuss Darcy's Law. Can anyone tell me how groundwater flows through soil?
I think it flows from high pressure to low pressure?
And maybe depending on how permeable the soil is?
Exactly! This brings us to Darcy's Law, which defines this flow mathematically. The equation is Q = -k A (dh/dl). Let's break that down!
Components of Darcy’s Law
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
In the equation Q = -k A (dh/dl), Q represents the discharge. Can anyone explain what discharge means in this context?
Isn't it the volume of water flowing through a specific area over time?
That's correct! Discharge measures how much water flows per second. Now, the 'k' in this equation represents the coefficient of permeability. Student_4, can you tell me what permeability means?
It's how easily fluids can pass through a porous material, right?
Exactly! It largely depends on the size and distribution of the pores in the material. Good job!
Assumptions of Darcy’s Law
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now let's talk about some assumptions of Darcy's Law. Why is the assumption of laminar flow important, Student_1?
I think laminar flow means the fluid is flowing smoothly, so it helps us use the equation without needing to account for turbulence?
You've got it! Turbulent flow could complicate calculations. Also, why must the environment be homogeneous and isotropic, Student_2?
If it's not, the fluid might flow differently in various parts, and our calculations would be inaccurate.
That's precisely the point! The consistency of the medium is crucial for predicting flow correctly.
Applications of Darcy’s Law
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Finally, let's explore the applications of Darcy's Law. Anyone know how it might be used in groundwater management?
It could help determine where to place wells or assess how much water can be extracted sustainably.
And it might also help in pollution studies, right? Like predicting how contaminants move through water layers!
Yes! By understanding the flow direction and rate, we can effectively manage and protect our water resources. Excellent contributions today!
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
This section introduces Darcy's Law, a fundamental principle in groundwater hydrology that defines how fluid flows through porous materials. It examines key components like discharge, permeability, and hydraulic gradient, as well as the assumptions necessary for the law to hold true.
Detailed
Overview of Darcy’s Law
Darcy's Law is a crucial equation in groundwater hydrology, providing insight into the flow rates of groundwater through various porous media.
Key Components of Darcy's Law
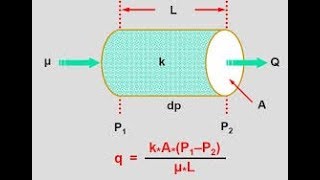
The law can be represented mathematically as:
\[ Q = -k A \frac{dh}{dl} \]
Where:
- \( Q \) = Discharge (m³/s)
- \( k \) = Coefficient of permeability (m/s)
- \( A \) = Cross-sectional area through which flow occurs (m²)
- \( \frac{dh}{dl} \) = Hydraulic gradient (the change in hydraulic head per unit length)
Assumptions of Darcy's Law
Darcy's Law is applicable under several key assumptions:
- Flow is laminar, ensuring smooth fluid movement.
- The porous medium must be homogeneous (uniform) and isotropic (properties are the same in all directions).
- The fluid (usually water) is incompressible and maintains a constant viscosity.
- The flow remains steady over time.
Importance in Groundwater Hydrology
Understanding Darcy's Law is essential for predicting groundwater movement, designing well systems, and ensuring sustainable water resource management.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Darcy's Law
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Darcy’s Law is a fundamental equation that describes the flow of groundwater through porous media.
Detailed Explanation
Darcy's Law provides a mathematical foundation for understanding how groundwater moves through soil and rock. The equation helps quantify the discharge of water moving through a porous medium, which is essential for various applications like groundwater management and environmental studies.
Examples & Analogies
Imagine trying to water your garden using different types of soil. In sandy soil, the water flows quickly, while in clay soil, it flows much slower. Darcy's Law helps us understand and predict how quickly water will flow through different types of soil, much like how you would water your plants based on the soil type.
Components of Darcy’s Law
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Q=−k A \[\frac{dh}{dl}\]
Detailed Explanation
The equation for Darcy’s Law consists of several important variables:
- Q represents the discharge, or how much water flows through an area over time.
- k is the coefficient of permeability, which shows how easily water can flow through a material.
- A is the cross-sectional area through which the water flows.
- The term \(\frac{dh}{dl}\) is the hydraulic gradient, indicating the change in hydraulic head per unit length. This gradient shows how steep the 'slope' of water levels is, guiding how fast the water will move.
Examples & Analogies
Think of a water slide in a theme park. The steepness of the slide determines how quickly you will reach the bottom. In this analogy, the hydraulic gradient is like the slide's steepness, and the water’s flow speed is comparable to the discharge (Q). The slide material (like rubber or plastic) represents the permeability (k).
Assumptions of Darcy's Law
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Assumptions of Darcy’s Law:
- The flow is laminar.
- The porous medium is homogeneous and isotropic.
- The fluid is incompressible and has constant viscosity.
- The flow is steady.
Detailed Explanation
Darcy's Law operates under certain assumptions that must be met for the law to accurately describe groundwater flow:
1. Laminar Flow: The flow of water is smooth and orderly, not chaotic.
2. Homogeneous and Isotropic Medium: The porous material has uniform properties in all directions, meaning the water will flow the same way regardless of where you measure it.
3. Incompressibility: The water's density does not change under pressure, simplifying calculations.
4. Steady Flow: Water flow remains consistent over time, allowing for predictable behavior.
Examples & Analogies
Think of a calm river flowing steadily on a flat path. If the water flows in a straight line without quick changes in direction (laminar), and the river bed is made of the same kind of rock everywhere (homogeneous and isotropic), then we can predict how quickly and where the water moves using Darcy’s Law.
Validity of Darcy's Law
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Darcy's law is valid for low Reynolds number flows (Re < 1), typical in most groundwater systems.
Detailed Explanation
The Reynolds number (Re) is a dimensionless value that helps predict flow patterns in fluids. For groundwater, Darcy's Law is applicable when Re is less than 1, indicating that the flow is smooth and laminar rather than turbulent. In typical groundwater systems, flow rates are low, which keeps the water movement consistent and predictable under the conditions outlined by Darcy's Law.
Examples & Analogies
Consider a slow-moving stream where leaves drift along the water surface without being kicked around too much. This represents low Re conditions. Should the stream's flow become faster and more aggressive, similar to a rapid river, then the leaves would whirl and spin, illustrating a transition to turbulent flow where Darcy’s Law might not hold as effectively.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Darcy’s Law: A fundamental theorem describing groundwater flow through porous materials.
-
Coefficient of permeability (k): Indicates how easily water flows through soil or rock.
-
Discharge (Q): Represents the volume of fluid passing through an area per unit time.
-
Hydraulic gradient (dh/dl): The slope of water levels indicating the direction of flow.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
If a well has a discharge of 10 m³/s and the cross-sectional area is 5 m², with a hydraulic gradient of 0.2, we can calculate the permeability.
-
In a sandy aquifer, the permeability may be high, allowing for greater discharge than in a clayey aquifer where permeability is low.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Water flows downhill, over earth and clay, Darcy's Law guides its way!
📖 Fascinating Stories
-
Imagine a water droplet on a hillside - it knows to flow where it's easiest, just like how Darcy's Law tells us groundwater moves through different soils based on their permeability.
🧠 Other Memory Gems
-
To remember Darcy's Law: 'Discharge Equals Permeability times Area times Gradient' (D = P × A × G).
🎯 Super Acronyms
D = P*A*G helps recall that Discharge is based on Permeability, Area, and Gradient.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Darcy's Law
Definition:
An equation that describes the flow of groundwater through porous media based on hydraulic gradient and permeability.
-
Term: Discharge (Q)
Definition:
The volume of groundwater flowing through a specific cross-sectional area per unit of time.
-
Term: Coefficient of permeability (k)
Definition:
A measure of how easily fluid can flow through a porous material.
-
Term: Hydraulic gradient (dh/dl)
Definition:
The change in hydraulic head per unit length, indicating the direction and magnitude of groundwater flow.
-
Term: Laminar flow
Definition:
A type of fluid flow where the fluid moves in smooth paths or layers, important for the application of Darcy's Law.
-
Term: Homogeneous
Definition:
A property of a medium where its characteristics are uniform throughout.
-
Term: Isotropic
Definition:
A property of a medium indicating that its characteristics are the same in all directions.
-
Term: Steady state
Definition:
A flow condition where the inflow and outflow remain constant over time.