Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Well Constants
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Today we'll explore well constants, key parameters derived from pumping test data that help us understand aquifer behaviors. Can anyone tell me why it's important to study these constants in groundwater hydrology?
I think it helps us know how much water we can extract from wells, right?
Exactly, Student_1! Well constants are fundamental in estimating sustainable yields for wells. They guide engineers in well design based on aquifer properties.
How do we derive these constants?
Great question! We derive well constants from pumping test data, often using the Theis equation. This downtime helps us model the drawdown in water levels over time.
What is the Theis equation, exactly?
The Theis equation looks like this: s equals W(u) over 4πT. Here, s represents drawdown and T is transmissibility. To dive deeper, we'll look at how it applies in actual scenarios. Remember the acronym WUT for We Understand Transmissibility in relation to drawdown!
Theis Equation in Practice
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Theis equation gets complex with its variables. Can anyone tell me how we would calculate 'u' in the equation?
Is it using r, S, T, and t?
That's correct, Student_4! Remember, 'u' is calculated as r²S over 4Tt— a crucial step in using the Theis equation effectively.
And how do we determine the drawdown?
We determine drawdown by observing changes in water levels from pre-pumping to post-pumping during our tests. It's vital to plot this data over time for analysis.
Is that where we plot time-drawdown data with type curves?
Exactly! Plotting helps match our curves to standard models like Theis or Jacob's method, allowing for meaningful comparisons and assessments.
Practical Applications of Well Constants
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
With our understanding of well constants, how can they assist in well design?
They help in figuring out how deep to drill to access enough water?
Absolutely, Student_3! Well constants indicate the aquifer's capacity and hence inform drilling depths. What factors do you think might limit well outputs?
I imagine if the aquifer is small or has low permeability, it wouldn’t supply much water?
Yes, those factors directly affect transmissibility and, subsequently, well yield. We must understand these relationships to develop sustainable groundwater management practices!
What are some examples of sustainable practices?
Examples include managing extraction rates based on constant monitoring of aquifers and implementing recharge areas to ensure groundwater sustainability.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
This section introduces well constants, derived from pumping test data, which are essential for evaluating aquifer characteristics. The Theis equation is highlighted as a method for understanding aquifer behavior and is crucial for effective well design and yield estimation.
Detailed
Well Constants
Well constants play a significant role in groundwater studies as they provide critical insights into the behavior of aquifers during pumping activities. These constants, derived from observed pumping test data, help in evaluating properties of the aquifer. The section discusses the Theis equation, which is instrumental under unsteady flow conditions.
Theis Equation
The Theis equation can be expressed as:
$$ s = \frac{W(u)}{4\pi T} $$
Where:
- s is the drawdown,
- Q is the discharge,
- T represents the transmissibility,
- W(u) is the well function, and
- u is a dimensionless parameter calculated as $$ u = \frac{r^2 S}{4 T t} $$ where r is the distance from the well and t is time.
Using time-drawdown data plots, scientists can estimate well constants and compare them with type curves like Theis or Jacob’s method. These constants are crucial for designing wells, estimating sustainable yields, and understanding aquifer behavior over time.
Youtube Videos
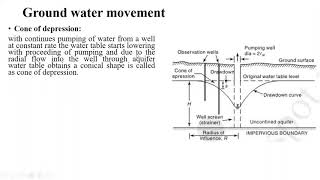
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Overview of Well Constants
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Well constants are derived from pumping test data and are used to evaluate the aquifer properties.
Detailed Explanation
Well constants are essential parameters that help understand the characteristics of an aquifer. They are obtained from data collected during pumping tests, which measure how a well behaves when water is removed from it. Essentially, these constants give us insight into how much water can be sustainably extracted from a well, contributing to the management and design of water supply systems.
Examples & Analogies
Think of well constants like a car's fuel efficiency rating. Just as you need to know how many miles you can drive per gallon to understand how far you can travel on a tank of gas, well constants help us determine how much water can be pulled from a well over time.
The Theis Solution
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Well function (Theis Solution): Applied for unsteady flow conditions.
Detailed Explanation
The Theis Solution is a mathematical approach used to analyze the data collected during pumping tests, particularly when the water level in the well drops due to pumping (unsteady flow). This solution helps determine how much drawdown occurs over time, which is critical in understanding the aquifer's response to increased water extraction.
Examples & Analogies
Imagine letting air out of a balloon; as you release air, the balloon shrinks. The Theis Solution helps predict how much a well's water level will drop as water is pumped out, similar to predicting the size of a balloon as air is let out.
Understanding the Theis Equation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Theis Equation: s = W(u) / (4πT) Where: s = Drawdown, Q = Discharge, T = Transmissibility, W(u) = Well function.
Detailed Explanation
The Theis Equation relates several important variables: drawdown (the decrease in water level), discharge (the volume of water taken from the well), transmissibility (how easily water can flow through the aquifer), and the well function (W(u)). This equation is used to quantify how much the water level in a well decreases when pumping occurs, allowing for the assessment of an aquifer's ability to deliver water.
Examples & Analogies
Think of this equation as a recipe for baking: the ingredients (drawdown, Q, T, W(u)) must be combined in the right proportions to find out how much water you get (drawdown). Just like a cake won't rise if the measurements are off, miscalculating these parameters can lead to unsustainable water extraction.
Calculating u in the Theis Equation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
u = r²S / (4Tt)
Detailed Explanation
In the context of the Theis Equation, 'u' is a dimensionless parameter that helps simplify calculations relating to drawdown. It incorporates the distance from the well (r), the drawdown (S), the transmissibility (T), and the time (t) of pumping. Understanding how to calculate 'u' is key to making the Theis Equation usable for real-world aquifer assessments.
Examples & Analogies
Calculating 'u' is like determining how long it takes to cook a meal based on the ingredients used and the cooking temperature. Just as you need to understand how these factors interact to predict cooking time, calculating 'u' helps predict drawdown based on aquifer characteristics and pumping duration.
Plotting Time-Drawdown Data
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Well constants can be obtained by plotting time-drawdown data and matching it with type curves (e.g., Theis or Jacob's method).
Detailed Explanation
To derive well constants effectively, hydrologists plot the drawdown of water levels over time during a pumping test. By comparing these plots with predefined type curves (known behaviors of wells), they can estimate the aquifer's properties. This graphical method allows for a visual assessment of how the aquifer responds to pumping and is crucial in well design and management.
Examples & Analogies
Imagine watching the stock market trends and comparing them to historical data. Just like investors analyze past performance to make future predictions, hydrologists use these curves to understand and anticipate how a well will behave, ensuring sustainable water management.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Well Constants: Key parameters derived from pumping test data.
-
Theis Equation: A formula describing drawdown under unsteady flow.
-
Transmissibility (T): Indicates the aquifer's capacity to transmit water.
-
Drawdown (s): The drop in water level caused by pumping.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
The Theis equation can be used to calculate drawdown at various distances from the well based on different pumping rates.
-
In an aquifer test, measuring drawdown over time can reveal insights into aquifer properties like transmissibility and storage.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
The Theis helps us see, how deep the flow can be!
📖 Fascinating Stories
-
Imagine a thirsty tree in a drought. The gardener measures how much water it can get over time using a special equation, ensuring the tree thrives without running dry.
🧠 Other Memory Gems
-
Remember WUT - Well Understanding Transmissibility to keep our aquifer happy!
🎯 Super Acronyms
USE - Understand, Sustain, Estimate for our groundwater well practices.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Well Constants
Definition:
Parameters derived from pumping test data used to evaluate aquifer properties.
-
Term: Theis Equation
Definition:
A formula used to describe drawdown in an aquifer under unsteady flow conditions.
-
Term: Transmissibility (T)
Definition:
The rate at which groundwater flows through a unit width of the aquifer under a unit hydraulic gradient.
-
Term: Drawdown (s)
Definition:
The decrease in hydraulic head in a well due to pumping.
-
Term: Well Function (W(u))
Definition:
A function used in the Theis equation representing drawdown over time.
-
Term: Dimensionless Parameter (u)
Definition:
A parameter calculated in relation to time, distance, and aquifer characteristics in the Theis equation.