Conclusion
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Velocity
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Welcome class! Today, we're concluding our chapter on motion. Let's start by revisiting the concept of velocity. What can anyone tell me about velocity?

Isn't velocity the same as speed?

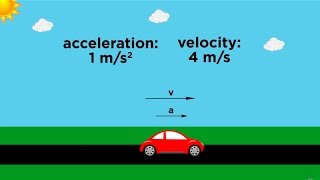
That's a great question! Velocity includes both speed and direction, making it a vector quantity. Speed is only how fast something moves; it lacks direction. Can anyone remember the formula for velocity?

It's displacement over time, right?

Exactly! Remember, displacement is the shortest distance from the initial to the final position. Let's add a memory aid: 'Velocity is Vector with Direction and Speed!' Can anyone give me an example of uniform and variable velocity?

Uniform would be a car moving straight at a constant speed, while variable could be a cyclist speeding up and slowing down.

Excellent! These examples help illustrate the differences. To sum up, velocity is crucial for understanding motion!
Acceleration Explained
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Next, let's discuss acceleration. Who can define it?

Isn't it the change in velocity over time?

Exactly right! Acceleration is also a vector quantity. It can indicate speeding up or slowing down. Can anyone recall the formula?

Change in velocity divided by time?

Correct! Remember the mnemonic: 'Acceleration Affects Velocity over Time.' Now, what real-life situations can you think of where acceleration is important?

Driving a car! It helps us to understand how quickly we can stop.

Great example! Acceleration plays a key role in transportation safety. Let's summarize: acceleration shows how velocity changes, which affects speed regulation in vehicles.
Linking Velocity and Acceleration
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now, let’s connect velocity and acceleration. How are they related?

If velocity changes, it must be due to acceleration.

Perfect! The equations of motion help us calculate using these relationships. Can someone list one of the equations for uniform acceleration?

V equals U plus At?

Yes! That's one important equation! Remember the acronym 'VUT' for Velocity = Initial Velocity + Acceleration × Time. Understanding these equations helps us predict motion. Can anyone share when these might be used in real life?

In sports, to measure an athlete's speed and changes in speed.

Exactly! These concepts apply in many areas like engineering and space exploration too. Quick recap: velocity changes due to acceleration, and they are quantifiable together through equations.
Graphical Representation
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now, let’s touch on graphical representations. Who's familiar with velocity-time graphs?

I've seen them! The slope tells us about acceleration.

Exactly! And the area under the curve gives us displacement. Mnemonic to remember: 'Slopes Signal Acceleration, Areas Account for Distance.' Can you think of scenarios where these graphs might be useful?

In analyzing race car speeds over time!

Spot on! Velocity-time graphs are crucial in motor sports. They help analyze performance. Quick summary: these graphs are valuable tools for visualizing motion dynamics.
Real-Life Applications
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Let's conclude by discussing real-life applications of velocity and acceleration. Can anybody share where this knowledge is applied?

In vehicle design and safety features.

Great example! Understanding these concepts ensures safety in many fields. We also see them in sports performance and even space exploration. Can anyone recall an example from sports?

In sprinting! Runners need to know their speed and how quickly they can accelerate.

Exactly! These concepts of motion apply everywhere in our lives. To cap it off, velocity and acceleration are essential for understanding motion, both in theory and practical applications. Well done today!
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
This section summarizes the key concepts of velocity as a vector quantity representing displacement over time and acceleration as the rate of change of velocity. It emphasizes the applicability of these concepts in real-world scenarios.
Detailed
Detailed Summary of Key Points
The conclusion of the chapter summarizes the essential concepts of velocity and acceleration. It reinforces that velocity is a vector quantity that indicates the rate of change of displacement with respect to time, incorporating both speed and direction. This is contrasted with speed, which is a scalar quantity. Additionally, acceleration is described as the rate of change of velocity over time, also a vector quantity. The relationship between velocity and acceleration is elucidated through equations of motion that provide a framework for understanding their interplay under uniform conditions. Furthermore, the importance of graphical representations is highlighted; velocity-time and acceleration-time graphs offer significant insights into motion dynamics, enabling calculations of displacement and acceleration. Finally, the practical applications of these concepts are acknowledged in various fields, such as transportation, sports, and engineering, demonstrating their relevance in our daily lives.
Youtube Videos






Audio Book
Dive deep into the subject with an immersive audiobook experience.
Summary of Key Points
Chapter 1 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Velocity is a vector quantity that represents the rate of change of displacement, and acceleration is the rate of change of velocity with respect to time.
Detailed Explanation
In this summary, we are reinforcing the essential definitions of two important concepts in physics: velocity and acceleration. Velocity is described as a vector quantity, which means it includes both a value (magnitude) and a direction. It measures how fast an object is changing its position. Acceleration, also a vector quantity, tells us how quickly the velocity of an object is changing. Understanding these definitions is critical as they form the foundation for the study of motion in physics.
Examples & Analogies
Think of driving a car. The speedometer shows how fast you are going (your velocity) and the steering wheel controls the direction of your car. If you press the accelerator, your car speeds up (increasing velocity), which is a result of acceleration. Thus, both concepts are at play when driving.
Equations of Motion
Chapter 2 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
The equations of motion under uniform acceleration provide a clear understanding of how velocity and displacement are related.
Detailed Explanation
The equations of motion describe the relationship between distance traveled (displacement), initial velocity, final velocity, acceleration, and time for objects moving under uniform acceleration. These equations allow us to calculate unknown variables if we know others. For example, if we know how fast an object is going initially, how much it speeds up or slows down (acceleration), and for how long, we can predict where it will be at a later time.
Examples & Analogies
Imagine you are on a roller coaster. You start from a specific point (initial velocity), as the coaster moves, it speeds up due to gravity (acceleration). By knowing how steep the hill is and how long the coaster travels down, we can predict its final speed and how far it has gone when it gets to the bottom.
Graphical Representation
Chapter 3 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
The graphical representation of velocity and acceleration helps visualize the motion and calculate displacement and acceleration.
Detailed Explanation
Graphs are a powerful tool in physics that allow us to visualize how an object's motion changes over time. A velocity-time graph can show us how fast an object is moving and how that speed changes. By looking at the slope of the graph, we can identify the object's acceleration. Moreover, the area under the graph can give us the displacement, or how far the object has traveled. This makes complex motion easier to understand and analyze.
Examples & Analogies
Consider watching a video of a car race. A velocity-time graph of the race would show spikes in velocity when the cars accelerate and drops when they slow down. Just like analyzing such a video gives insight into the race dynamics, the graphs translate that motion into a format we can analyze easily.
Practical Applications
Chapter 4 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Practical applications of these concepts are widespread, especially in fields like transportation, sports, and engineering.
Detailed Explanation
Velocity and acceleration concepts are fundamental in various real-world applications. In transportation, knowing how fast vehicles need to go and how quickly they can stop is crucial for safety. Engineers apply these principles when designing vehicles, ensuring that they can accelerate and decelerate efficiently. In sports, these concepts are used to improve athlete performance by analyzing how quickly they can move and change speeds.
Examples & Analogies
Think about a sprinter during a race. Coaches use velocity and acceleration to develop training programs that improve the runner's speed and agility. By understanding how fast and how much they can accelerate, they can predict performance and determine the best strategies for winning.
Key Concepts
-
Velocity: A vector quantity indicating displacement over time.
-
Acceleration: The change in velocity over time, also vector in nature.
-
Uniform Motion: Motion at a constant velocity.
-
Non-uniform Motion: Motion with changing velocity.
-
Graphical Representation: Visual analysis of motion dynamics through graphs.
Examples & Applications
A car traveling from one city to another at a constant speed for 2 hours exhibits uniform velocity.
An athlete sprinting and changing speed during a race demonstrates variable velocity and acceleration.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
To find velocity's might, just look for its direction and its height.
Stories
Imagine a car that drives straight at a constant speed. It never turns, and that's uniform velocity, while a bicycle riding through a park changes speed is variable velocity.
Memory Tools
For acceleration: 'Affects' is for the change, 'Velocity' goes through its range.
Acronyms
VUT
Velocity = Initial Velocity + Acceleration × Time.
Flash Cards
Glossary
- Velocity
A vector quantity representing the rate of change of displacement with respect to time, indicating both speed and direction.
- Acceleration
The rate of change of velocity with respect to time, also a vector quantity, indicating how quickly an object's velocity changes.
- Displacement
The shortest straight-line distance from an object's initial position to its final position, with direction.
- Uniform Velocity
When an object's velocity remains constant over time.
- Variable Velocity
When an object's velocity changes with time.
- Uniform Acceleration
When an object's acceleration is constant over a period of time.
- Nonuniform Acceleration
When an object's acceleration changes over time.
Reference links
Supplementary resources to enhance your learning experience.
