What is Acceleration?
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Acceleration
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Welcome, everyone! Today we'll be diving into the concept of acceleration. Can anyone tell me what they think acceleration means?

Isn't it how fast something speeds up?

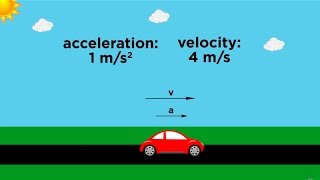
That's correct! Acceleration is indeed the rate at which an object's velocity changes over time. It's a vector, meaning it has both magnitude and direction.

So, does it mean that if an object slows down, it’s still acceleration?

Yes, absolutely! Acceleration can indicate that an object is speeding up or slowing down. In physics, we often refer to slowing down as negative acceleration or deceleration.

Can you remind us how we express acceleration mathematically?

Certainly! The formula for acceleration is given by \[ a = \frac{v - u}{t} \], where \( v \) represents the final velocity, \( u \) the initial velocity, and \( t \) the time interval.

What are the units we use for acceleration?

Great question! The SI unit for acceleration is meters per second squared, or m/s². This unit reflects how much the velocity changes in a second.

In summary, acceleration is about how quickly an object's velocity is changing, and it’s very important in analyzing motion. Let's explore its different types in our next session.
Types of Acceleration
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now that we've understood what acceleration is, let's talk about types of acceleration. Who can tell me about them?

I think there’s something called uniform acceleration?

Exactly! Uniform acceleration occurs when the change in velocity is constant over time, meaning an object accelerates at the same rate. Can you think of an example where this happens?

Maybe a car that speeds up at a steady rate?

Correct! And on the flip side, we have non-uniform acceleration, where the rate of change varies. Can anyone provide an example of that?

How about a roller coaster? It slows down and speeds up at different points.

That's a perfect example! Non-uniform acceleration is common in real-life scenarios. So remember: uniform acceleration is steady, while non-uniform is unpredictable.

Doesn't that also affect how we calculate motion?

Absolutely! The type of acceleration influences the way we apply the equations of motion. Keep this in mind as we move forward.

Let's recap: uniform acceleration is constant while non-uniform varies. Understanding these helps us predict motion correctly.
Application of Acceleration
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

We've learned a lot about acceleration. Let's discuss why it matters in the real world. Can anyone share an example where understanding acceleration is crucial?

I think vehicles need to understand acceleration for safety measures?

Correct! Vehicles rely on acceleration data to determine stopping distances and acceleration profiles.

What about in sports? I’ve seen athletes monitored for their speed during races.

Exactly! In sports, analyzing acceleration can help improve performance. Coaches use this data to strategize training.

And in space exploration, right? Isn’t acceleration used to calculate spacecraft velocities?

Yes! Space missions rely heavily on accurate calculations of acceleration to navigate and execute maneuvers in outer space.

To summarize, acceleration is not just a theoretical concept; it has real implications in our daily lives and technological advancements.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
In this section, we explore the definition and concepts of acceleration as a vector quantity, the formulas used for calculations, the various types of acceleration, and its significance in understanding motion. The section elaborates on the implications of acceleration in real-world scenarios and provides numerical examples for better comprehension.
Detailed
What is Acceleration?
Acceleration is defined as the rate of change of velocity concerning time, making it a vector quantity. This means it has both magnitude and direction, indicating whether an object is speeding up or slowing down. The formula for calculating acceleration is:
\[ a = \frac{v - u}{t} \]
Where:
- a = acceleration
- v = final velocity
- u = initial velocity
- t = time taken
In the SI unit system, acceleration is measured in meters per second squared (m/s²), illustrating how much the velocity changes per second. The section covers two primary types of acceleration:
1. Uniform Acceleration: Consistent acceleration over time.
2. Non-uniform Acceleration: Fluctuating acceleration with time.
Understanding acceleration is essential, as it relates directly to velocity changes, and this link is critical in formulated equations of motion that help predict and analyze moving objects.
Youtube Videos






Audio Book
Dive deep into the subject with an immersive audiobook experience.
Definition of Acceleration
Chapter 1 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Acceleration is the rate of change of velocity with respect to time. It is a vector quantity, meaning it has both magnitude and direction.
Acceleration indicates how quickly an object’s velocity is changing—whether the object is speeding up or slowing down.
Detailed Explanation
When we discuss acceleration, we're talking about how fast the speed of an object increases or decreases over a period of time. Since acceleration is a vector quantity, it doesn't just have a size (how much) but also a direction (where). This means that if a car accelerates to the right at a certain speed, it is very different from a car accelerating to the left at the same speed. When we say an object is accelerating, it can mean it is speeding up (increasing velocity), slowing down (decelerating), or changing direction.
Examples & Analogies
Imagine you're riding a bicycle. If you start pedaling faster, you're accelerating—you feel like you're getting pushed back into your seat. If you apply the brakes, you're also accelerating, but in the opposite direction, causing you to slow down. Thus, acceleration can happen in different scenarios besides just speeding up—it's any change in your velocity.
Formula for Acceleration
Chapter 2 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
The formula for acceleration is given as:
Acceleration = Change in velocity / Time taken
Or,
a = (v - u) / t
Where:
- a = acceleration
- v = final velocity
- u = initial velocity
- t = time taken
Detailed Explanation
The formula for acceleration helps us calculate how much an object's velocity changes over time. Here, 'v' refers to the final velocity the object reaches. 'u' is its initial velocity, or its speed before acceleration starts. 't' is the time over which this change occurs. By subtracting the initial velocity from the final velocity, we find out how much the velocity has changed. Then, we divide that change by the time to determine the acceleration—the rate at which the velocity changes every second.
Examples & Analogies
Think about a car at a traffic light. If it starts from rest (u = 0) and speeds up to 30 m/s (v) in 5 seconds (t), we can calculate its acceleration. Using the formula, we get:
a = (30 m/s - 0) / 5 s = 6 m/s².
This means every second, the car's velocity increases by 6 meters per second, showcasing how quickly it's speeding up!
Units of Acceleration
Chapter 3 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
In the SI system, the unit of acceleration is meters per second squared (m/s²).
This unit represents the change in velocity (m/s) per second.
Detailed Explanation
The unit of acceleration tells us how quickly an object's velocity changes. When we say an object has an acceleration of 1 m/s², it means that for every second that passes, the object's velocity increases by 1 meter per second. So if it starts at rest, after one second it will be traveling at 1 m/s, after two seconds at 2 m/s, and so forth. It's an important concept because it lets us quantify how quickly speed changes.
Examples & Analogies
Consider a roller coaster. If it accelerates at a rate of 2 m/s², it doesn't just reach a high speed instantly; every second, it's going faster and faster. After 5 seconds, if it started from rest, it would be moving at 10 m/s (2 m/s² * 5 s), making that thrilling feeling of speed clear and tangible!
Types of Acceleration
Chapter 4 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
- Uniform Acceleration: When an object’s acceleration is constant over time, it is said to have uniform acceleration.
- Non-uniform Acceleration: When an object’s acceleration changes with time, it is said to have non-uniform acceleration.
Detailed Explanation
Acceleration can be consistent or variable. With uniform acceleration, an object like a car might steadily increase its speed, say by accelerating at 2 m/s², meaning it adds 2 m/s to its speed every second without changing that rate. On the other hand, non-uniform acceleration involves changes in how quickly the speed increases or decreases. For example, a car might accelerate at 2 m/s² for a few seconds, then increase to 3 m/s², and later decelerate. Recognizing these two types helps us understand different motion scenarios.
Examples & Analogies
Imagine a sprinter in a race. If she starts slow and gradually picks up her speed, moving faster each second with a consistent increase, that's uniform acceleration. But if she speeds up dramatically while approaching the finish line and slows down to catch her breath shortly after, that's non-uniform acceleration. This differentiation helps in analyzing performance and improving techniques in sports.
Key Concepts
-
Acceleration: The rate of change of velocity over time.
-
Uniform Acceleration: Constant change in velocity.
-
Non-uniform Acceleration: Variable change in velocity.
-
SI Unit for Acceleration: Meters per second squared (m/s²).
Examples & Applications
A car accelerates from 20 m/s to 30 m/s in 5 seconds, demonstrating uniform acceleration.
A falling object like a skydiver experiences non-uniform acceleration due to air resistance changing their velocity over time.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
To know acceleration, just keep in mind, it's velocity’s change, a rate defined.
Stories
Imagine a race car zooming down the track—at first slow, then vroom, it speeds up to the max! That's acceleration in action!
Memory Tools
For acceleration, remember: A for Average (change in velocity), T for Time (like how long it takes), M for Meters per second squared (the unit).
Acronyms
A.V.T. => Acceleration = Velocity change / Time
Flash Cards
Glossary
- Acceleration
The rate of change of velocity per unit of time, represented as a vector quantity.
- Uniform Acceleration
A constant rate of acceleration with no change over time.
- Nonuniform Acceleration
A varying rate of acceleration that changes over time.
- Velocity
A vector quantity that indicates the rate of change of displacement with direction.
- SI Unit
The International System of Units, with meters per second squared (m/s²) as the unit of acceleration.
Reference links
Supplementary resources to enhance your learning experience.
