Introduction to Velocity and Acceleration
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Velocity
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today, we're diving into the concept of velocity. Who can tell me what velocity is? Remember, it’s not just speed!

Isn't velocity just how fast something is going?

Good start! But it's more specific than just speed—it’s a vector quantity, meaning it includes direction. The formula for velocity is displacement divided by time. Can anyone tell me what displacement means?

Is displacement just the distance traveled?

Not exactly! Displacement is the shortest distance from the starting point to the endpoint. Now, let's explore the units of velocity. What’s the SI unit for velocity?

I think it’s meters per second, m/s?

Correct! And you can also express it in kilometers per hour. To remember the key differences, think 'S = speed, D = direction' for velocity. Remember, symmetry in your understanding!

What are the types of velocity?

Great question! We have uniform velocity, which stays constant, and variable velocity, which changes. Any last questions before we summarize?

Can we summarize that quickly?

Absolutely! Velocity is a vector quantity defined as displacement over time, with types being uniform and variable. Remember that its unit is m/s.
Understanding Acceleration
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now onto acceleration. Who can tell me what acceleration is?

Is it how fast something speeds up?

Excellent! Acceleration is indeed the rate of change of velocity. It also has a direction, making it a vector. Can anyone share how we calculate acceleration?

Is it change in velocity over time?

Yes! We can represent this as: $$Acceleration = \frac{Change \ in \ velocity}{Time}$$. What do we use as our units here?

Meters per second squared, right?

That's right! Now, acceleration can be uniform or non-uniform. Can anyone clarify the difference?

Uniform is when acceleration stays the same?

Right! And non-uniform means it changes over time. Before we summarize, does anyone have any further questions?

Can we quickly review the formula one last time?

Sure! Acceleration is calculated as the change in velocity divided by time, with its unit being m/s². Remember, acceleration is a change, and velocity is the movement.
Relationship between Velocity and Acceleration
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now, let’s examine how velocity and acceleration are tied together. If velocity changes, what does that tell us about acceleration?

It must be accelerating!

Exactly! So, when we talk about their relationship, we often refer to the equations of motion. Who remembers the first one?

Is it $$v = u + at$$?

Correct! That's the final velocity formula. Who can explain what it represents?

It shows that final velocity equals initial velocity plus acceleration times time.

Well done! The other two equations involve displacement. Can someone share the second one?

Is it $$s = ut + \frac{1}{2}at^2$$?

Exactly! This relates displacement to both initial velocity and acceleration. Finally, let's recognize that these equations help us analyze motion effectively. Summary, anyone?

Velocity changes due to acceleration, and we can use the equations of motion to describe that.

Excellent summary! Remember these connections, they are vital for understanding motion!
Graphical Representation
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now, let’s visualize what we’ve learned through graphs! Who knows how a velocity-time graph can represent motion?

I think the slope of the graph indicates acceleration?

Absolutely! A steeper slope indicates greater acceleration. What about the area under the graph?

That would show the total displacement, right?

Exactly! Now, what about an acceleration-time graph? What kind of information does that convey?

It shows how acceleration changes over time?

Correct! A horizontal line indicates constant acceleration; a varying line shows changing acceleration. Each graph serves a specific purpose in analyzing motion. Let’s conclude with a quick recap. What’s key about these graphs?

The slope tells us about acceleration, and the displacement is found under the velocity graph.

Perfect! Remembering this will enhance your understanding of motion significantly!
Applications of Velocity and Acceleration
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

To connect our learning with real life, let’s discuss practical applications of velocity and acceleration. Can anyone think of areas where these play a critical role?

Vehicles need to understand these concepts for safety and efficiency.

Absolutely! Understanding both helps with stopping distances and vehicle design. Any other fields?

In sports, athletes analyze speed and acceleration to improve performance!

Good point! Sports science heavily relies on these calculations. And what about space exploration?

Spacecraft must manage their velocity and acceleration for safe travel and maneuvers.

Spot on! These concepts are everywhere, from roads to space! Let’s finalize by summarizing key applications.

We see velocity and acceleration in vehicles, sports, and space missions.

Exactly! These concepts are pivotal in various fields, enhancing our understanding of motion.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
Velocity is defined as a vector quantity that measures the rate of change of displacement over time, incorporating both speed and direction. Acceleration is similarly a vector quantity, indicating the rate of change of velocity over time. This section covers the respective formulas, types of each concept, and their implications in real-world applications.
Detailed
Introduction to Velocity and Acceleration
This section serves as a foundational introduction to velocity and acceleration, which are fundamental concepts in physics describing motion.
Understanding Velocity
- Definition: Velocity is a vector quantity indicating the rate of change of displacement concerning time. Unlike speed, which only expresses how fast an object is moving, velocity includes the direction of the object's motion.
- Formula: The formula for velocity is given by
$$Velocity = \frac{Displacement}{Time}$$
where displacement is the shortest distance between the start and end points, and time is the duration of this change. - Units: In SI units, velocity is measured in meters per second (m/s) but can also be expressed in kilometers per hour (km/h) for different contexts.
- Types: Two main types of velocity exist:
- Uniform Velocity: Constant speed and direction.
- Variable Velocity: Speed and/or direction change over time.
Understanding Acceleration
- Definition: Acceleration is a vector quantity that measures how quickly an object's velocity changes over time. It can represent both speeding up and slowing down motion.
- Formula: It is calculated using the formula
$$Acceleration = \frac{Change \ in \ velocity}{Time \ taken}$$
or
$$a = \frac{v - u}{t}$$
where - a = acceleration
- v = final velocity
- u = initial velocity
- t = time taken
- Units: The SI unit of acceleration is meters per second squared (m/s²).
- Types: The acceleration can also be classified into:
- Uniform Acceleration: Constant acceleration over time.
- Non-uniform Acceleration: Varies over time.
Relationship Between Velocity and Acceleration
Velocity and acceleration are directly interconnected since a change in velocity implies acceleration. The equations of motion under uniform acceleration provide critical relationships:
- $$v = u + at$$ (Final velocity)
- $$s = ut + \frac{1}{2}at^2$$ (Displacement)
- $$v^2 = u^2 + 2as$$ (Kinematics equation)
Graphical Representation
- Velocity-Time Graphs illustrate motion where the slope represents acceleration and the area under the graph gives displacement.
- Acceleration-Time Graphs represent changes in acceleration over time, with horizontal lines indicating constant acceleration.
This section provides a basis for understanding motion concepts essential in practical applications, such as vehicle dynamics, sports performance, and engineering.
Youtube Videos




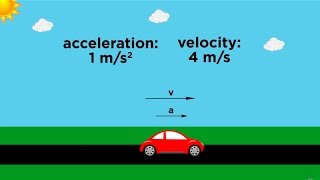


Audio Book
Dive deep into the subject with an immersive audiobook experience.
What is Velocity?
Chapter 1 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
● Velocity is a vector quantity that refers to the rate of change of displacement with respect to time. It gives both the speed of an object and the direction of its motion.
Detailed Explanation
Velocity tells you not just how fast something is moving, but also in which direction. For example, if a car is moving at 60 km/h eastwards, it has both speed (60 km/h) and a direction (eastwards). This makes velocity a vector quantity, distinguishing it from speed, which only provides the magnitude of movement.
Examples & Analogies
Imagine you're driving a car. If you say you're going 60 km/h, that's speed. But if you say you're going 60 km/h to the north, that's velocity. Knowing the direction can change everything, especially on a road trip!
Difference Between Velocity and Speed
Chapter 2 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
● It is different from speed because speed is a scalar quantity, which only refers to how fast an object is moving, whereas velocity provides both magnitude (speed) and direction.
Detailed Explanation
Speed refers to how fast an object is moving, regardless of its direction. Since speed does not involve direction, it is called a scalar quantity. For instance, saying an object is moving at 50 km/h gives the speed but does not specify where it's headed, unlike velocity, which would specify both speed and direction.
Examples & Analogies
Think of a marathon runner. If someone says the runner is going 10 km/h, they’re talking about speed. But if they say the runner is moving at 10 km/h toward the finish line, that’s velocity—and it’s much clearer!
Formula for Velocity
Chapter 3 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
● The formula for velocity is given as:
Velocity = Displacement / Time
Where:
○ Displacement is the shortest distance between the initial and final positions of an object.
○ Time is the duration taken for the displacement.
Detailed Explanation
To calculate velocity, you take the total displacement (the shortest distance in a straight line from start to finish) and divide it by the time it took to cover that distance. This gives you a speed with a direction. If you ran 100 meters north in 10 seconds, your velocity would be 10 meters/second north.
Examples & Analogies
Envision throwing a ball straight up. If it reaches a height of 20 meters and comes back down in 4 seconds, we can calculate the velocity by finding out its displacement (20 meters) divided by time (4 seconds), which is 5 m/s upwards.
Units of Velocity
Chapter 4 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
● In the SI system, the unit of velocity is meters per second (m/s).
● The unit of velocity can be converted depending on the situation. For example, in cases involving longer distances, kilometers per hour (km/h) might be used.
Detailed Explanation
Velocity is measured in units such as meters per second (m/s) in the International System of Units (SI). However, depending on the context, we might use kilometers per hour (km/h), especially when discussing vehicles and travel over longer distances. It's important to know both units to understand the speed in different situations.
Examples & Analogies
If you're driving a car, the speedometer shows speed in km/h; you'd say it's traveling at 80 km/h. But if you're calculating a short jog, you might want to note your speed in m/s because the distance is shorter. Just like how cooking might require grams versus kilograms!
Types of Velocity
Chapter 5 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
● Types of Velocity
1. Uniform Velocity: When an object moves with the same velocity in a straight line, it is said to have uniform velocity.
2. Variable Velocity: When an object’s velocity changes with time, it is said to have variable velocity.
Detailed Explanation
Uniform velocity is when an object moves at a constant speed in a straight line, meaning it doesn’t change direction or speed. In contrast, variable velocity occurs when the speed or direction changes, such as when a car accelerates or turns a corner.
Examples & Analogies
Consider a train moving at a constant speed on a straight track—this is uniform velocity. Now think of a bike rider speeding up as they go downhill; their speed is changing, which is a variable velocity. Just like how the smooth highway ride is different from the winding roads in the hills!
Key Concepts
-
Velocity: a vector quantity measuring the rate of displacement change.
-
Acceleration: the change in velocity over time, also a vector quantity.
-
Displacement: the shortest distance between initial and final positions.
-
Uniform and Variable Velocity: consistency versus change in speed.
-
Uniform and Non-uniform Acceleration: constant versus changing acceleration.
-
Equations of Motion: mathematical relations involving displacement, velocity, and acceleration.
-
Graphical Representation: visualizing motion through graphs.
Examples & Applications
A car moving in a straight line at a constant speed of 60 m/s demonstrates uniform velocity.
A cyclist speeds up from 10 m/s to 20 m/s in 5 seconds showing acceleration.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
Velocity so fast and true, direction matters, it's not just you!
Stories
Imagine a racecar zooming around a track. Its speed and direction are crucial—if it turns sharply, that's where velocity shines. It describes not just how fast it goes, but where it heads!
Memory Tools
For velocity, remember 'Speed + Direction = Vector' (SDV).
Acronyms
VADS for remembering Velocity
(V)ector
(A)cceleration
(D)isplacement
(S)peed.
Flash Cards
Glossary
- Velocity
A vector quantity representing the rate of change of displacement with respect to time, incorporating both speed and direction.
- Acceleration
The rate of change of velocity concerning time, also a vector quantity indicating how quickly an object's velocity changes.
- Displacement
The shortest distance from the initial position to the final position of an object.
- Uniform Velocity
When an object moves with a constant velocity in a straight line.
- Variable Velocity
When an object’s velocity changes over time.
- Uniform Acceleration
Constant acceleration over time.
- Nonuniform Acceleration
Acceleration that changes over time.
- Equations of Motion
Mathematical formulas that relate displacement, velocity, and acceleration.
- VelocityTime Graph
A graph used to represent an object's velocity over time, where the slope indicates acceleration, and the area represents displacement.
- AccelerationTime Graph
A graph showing how acceleration changes with time.
Reference links
Supplementary resources to enhance your learning experience.
