Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skillsβperfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
Youβve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take mock test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Initial and Final Velocity
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Today, we'll discuss the first equation of uniformly accelerated motion: \( v = u + at \). Can anyone tell me what \( u \) and \( v \) stand for?
I think \( u \) is the initial velocity, right?
Exactly! \( u \) is the initial velocity, and \( v \) is the final velocity. This equation shows how velocity changes over time due to acceleration. Can anyone give me an example of how this might apply?
If a car starts from rest, that means its initial velocity is 0, right?
Yes! In that case, if it accelerates, we can use this equation to find the final velocity after a certain time. Remember: If you're calculating, listing your known values helps track your work!
So, if it accelerates at 3 m/sΒ² for 5 seconds, it will change its velocity?
Correct! Using \( v = 0 + (3)(5) \), we find \( v = 15 \) m/s. Great thinking!
So, can we use this equation to predict the car's speed at any time in its acceleration phase?
Absolutely! That's the beauty of these equations. Let's summarize: The first equation relates initial velocity, acceleration, and time to find final velocity.
Displacement Analysis
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now let's discuss the displacement equation: \( s = ut + \frac{1}{2}at^2 \). What does \( s \) represent?
It represents the displacement traveled during the time of acceleration, doesn't it?
Exactly! This equation shows how to calculate total displacement using initial velocity, time, and acceleration. Letβs plug some numbers in. If a bike with an initial speed of 2 m/s accelerates at 4 m/sΒ² for 3 seconds, how do we find \( s \)?
So weβd calculate it as \( s = (2)(3) + \frac{1}{2}(4)(3^2) \)?
Perfect! Let's calculate that: \( s = 6 + \frac{1}{2}(4)(9) = 6 + 18 = 24 \) meters.
Does that mean the total distance the bike travels after 3 seconds is 24 meters?
You got it! Remember, calculating accurately lets us predict where an object will be during its motion. Summarizing: This equation is vital for determining how far an object moves under uniform acceleration.
Velocity and Displacement Relationship
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
The third equation weβll cover is \( v^2 = u^2 + 2as \). This relates the final velocity squared to the initial velocity squared, with displacement and acceleration as components. What could we calculate with this equation?
We can find how fast an object is moving when we know its acceleration and the distance it covered!
Exactly! Suppose a runner starts with an initial velocity of 2 m/s, accelerates at 2 m/sΒ² for a distance of 50 meters. What would be their final velocity?
I think we can rearrange the equation to find \( v \). So, \( v^2 = 2^2 + 2(2)(50) \)?
Correct! Now whatβs the next step?
That will give us \( v^2 = 4 + 200 = 204 \), so \( v = \sqrt{204} \) which is about 14.28 m/s!
Excellent work! Remember, this equation is valuable for finding relationships between velocity, acceleration, and distance. Letβs summarize: We can calculate the final velocity by knowing the initial velocity, acceleration, and displacement.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The equations of uniformly accelerated motion describe the relationship between displacement, velocity, acceleration, and time. The three primary equations are presented, which are essential for understanding the kinematics of objects under constant acceleration.
Detailed
Equations of Uniformly Accelerated Motion
This section introduces the equations used to depict uniformly accelerated motionβan essential concept in kinematics that excludes forces acting on objects. These equations are significant for solving problems related to motion, enabling students to predict an object's position and velocity over time.
Key Equations
- Final Velocity Equation:
\( v = u + at \) -
Where:
- \( v \): final velocity
- \( u \): initial velocity
- \( a \): acceleration
- \( t \): time
-
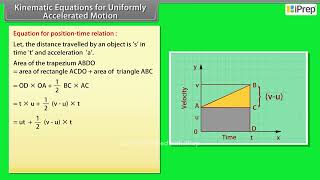
Displacement Equation:
\( s = ut + \frac{1}{2}at^2 \) -
Where:
- \( s \): displacement
-
Velocity-Displacement Equation:
\( v^2 = u^2 + 2as \)
Significance
These equations allow students to analyze motion in various scenarios, enhancing their problem-solving skills in physics. Mastery of uniformly accelerated motion equations is foundational for deeper study in physics.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Equation for Final Velocity
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
v = u + at
Detailed Explanation
This equation helps us understand how the final velocity (v) of an object changes over time based on its initial velocity (u), acceleration (a), and the time period (t) over which the object is accelerating. In simpler terms, if you know how fast an object was moving at the start (u) and how quickly it is speeding up (a), you can find out how fast it will be moving after a certain amount of time (t).
Examples & Analogies
Imagine a car that starts from rest (initial velocity, u = 0) and accelerates at a rate of 5 meters per second squared (a = 5 m/sΒ²). After 3 seconds (t = 3), its final speed can be calculated using this equation: v = 0 + (5 * 3) = 15 m/s. So, after 3 seconds, the car will be going 15 meters per second.
Equation for Displacement
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
s = ut + Β½atΒ²
Detailed Explanation
This equation calculates displacement (s), which is how far an object has moved from its original position, considering both its initial velocity (u) and how much it accelerates (a) over a period of time (t). The term 'ut' represents the distance traveled at the initial velocity, while 'Β½atΒ²' accounts for the additional distance gained due to acceleration.
Examples & Analogies
Think of a ball rolling down a hill. Letβs say it starts rolling at an initial speed of 2 meters per second and accelerates by 4 meters per second squared. After 5 seconds, we can determine how far it has traveled using the equation. The initial distance would be 2 m/s * 5 s = 10 m from the start, plus the extra distance gained due to acceleration, which is Β½ * 4 m/sΒ² * (5 s)Β² = 50 m. So, the total displacement is 10 m + 50 m = 60 m.
Equation Relating Velocities and Displacement
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
vΒ² = uΒ² + 2as
Detailed Explanation
This equation connects the squares of the initial and final velocities (u and v) along with the acceleration (a) and the displacement (s). It shows how the velocities are related when an object accelerates over a specific distance. This equation is especially useful when you don't know the time of the motion but have the initial and final speeds and the distance covered.
Examples & Analogies
Picture a rollercoaster that starts from a certain height. If you know the initial speed at the top (u), how fast the rollercoaster goes down (uΒ² + 2as) as it accelerates down the track, you can find out its speed (v) at the bottom without needing to consider how long it took. For example, if the coaster starts from rest (u = 0) and drops down a vertical distance of 20 meters with an acceleration due to gravity (about 10 m/sΒ²), you can find its speed at the bottom: vΒ² = 0 + 2 * 10 * 20, so vΒ² = 400, thus v = 20 m/s.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Initial velocity (u): The starting speed of an object before acceleration.
-
Final velocity (v): The speed of an object at the end of the acceleration.
-
Acceleration (a): The change in velocity per unit time, affecting how fast an object speeds up or slows down.
-
Time (t): Duration over which the motion occurs, affecting displacement and velocity.
-
Displacement (s): Total distance traveled in a specific direction during motion.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
A car accelerates from 0 m/s to 20 m/s in 10 seconds; find its acceleration.
-
A ball is thrown upward with an initial velocity of 15 m/s; calculate how high it goes before stopping.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
π΅ Rhymes Time
-
When speed ups and downs we measure, remember time and distance as a treasure.
π Fascinating Stories
-
Once upon a time, a car started at a speed of 'u'. With pedal to the metal, it accelerated to speed 'v' with a push of 'a', all within a time 't'. The journey was magical, and you could calculate how far 's' it would go easily!
π§ Other Memory Gems
-
A simple phrase: SVD - Speed, Velocity, Displacement, reminds us what equations measure in motion.
π― Super Acronyms
Using 'VAT', recall
- **V**elocity = **A**cceleration x **T**ime + Initial Velocity
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Initial Velocity (u)
Definition:
The velocity of an object at the beginning of the observation or time period.
-
Term: Final Velocity (v)
Definition:
The velocity of an object at the end of the observation or time period.
-
Term: Acceleration (a)
Definition:
The rate at which an object changes its velocity, measured in meters per second squared (m/sΒ²).
-
Term: Displacement (s)
Definition:
The shortest distance from the initial position to the final position of an object, including direction.
-
Term: Time (t)
Definition:
The duration over which motion occurs, measured in seconds.