Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skillsβperfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
Youβve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take mock test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Recursion
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Today, we're going to explore recursion, a powerful concept in programming where a function calls itself. Can anyone tell me what you think recursion means?
I think itβs when a function repeats itself?
Exactly! It's a method of solving problems where a function calls itself to tackle smaller instances of the same problem. Now, what do you think is crucial for a recursive function to work properly?
It needs to have a stopping point?
Correct! Thatβs called the base case. Without it, the function would run indefinitely. Can anyone provide an example of a problem that might use recursion?
How about calculating the factorial of a number?
Great example! Factorial is indeed a classic case of recursion. To recap, recursion involves a base case that terminates the function and a recursive case that continues the process.
Characteristics of Recursion
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Let's dive deeper into the two main characteristics of recursion. Can anyone remind me what they are?
Base case and recursive case?
Exactly! The base case must be defined to prevent infinite loops. Now, what happens when we reach the base case?
The function stops calling itself!
Right! And do you remember what we call the process of returning values once the base case is reached?
Stack unwinding?
Perfect! All values are returned back in reverse order, ensuring the calculations are properly completed.
Types of Recursion
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now, letβs differentiate between types of recursion. Who can tell me the difference between direct and indirect recursion?
Direct recursion is when a function calls itself?
Correct! And indirect recursion?
Itβs when one function calls another that eventually calls the first one?
That's right! Indirect recursion can be more complex, but both types have their applications. Can you think of real-world situations where recursion might be advantageous?
Like categorizing files in a directory?
Excellent point! Recursion is great for tasks like that, as well as solving puzzles, backtracking algorithms, and more.
Examples of Recursion
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Letβs look at some actual examples. Who remembers how to calculate the factorial using recursion?
Yes! Itβs something like if n is 0, return 1; else return n times factorial of n minus 1.
Exactly! Great job. Now, what about the Fibonacci series? Can we write a recursive function for that?
It's similar, right? Like, if n equals 0 return 0, if n equals 1 return 1, else return the sum of the previous two Fibonacci numbers!
Yes! You all are catching on fast. These examples show how recursion can simplify complex calculations.
Advantages and Disadvantages of Recursion
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Finally, let's discuss the advantages and disadvantages of recursion. Can anyone start with an advantage?
It makes the code cleaner and easier to understand.
Absolutely! What about a disadvantage?
It might lead to stack overflow if the recursion goes too deep.
Thatβs correct! While recursion is powerful, it can be inefficient in some cases, especially concerning memory usage. So, always consider whether recursion is the best approach for your problem.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
What is Recursion?
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Recursion occurs when a function calls itself within its own body to solve a smaller instance of the same problem. The process continues until it reaches a base case, which stops the recursion.
Detailed Explanation
In recursion, a function solves a complex problem by breaking it down into smaller, more manageable problems. The function calls itself until it reaches a predefined condition known as the base case, which tells the function to stop calling itself further. This approach allows programmers to express solutions to problems in a more intuitive way, where each recursive call works towards solving a smaller part of the original problem.
Examples & Analogies
Imagine you are nesting dolls, where each doll contains a smaller one inside. To reach the smallest doll, you would open each one until you find the last doll β this process is similar to recursion, where the function keeps calling itself until it hits the smallest doll, or the base case.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Base Case: Necessary for stopping recursion.
-
Recursive Case: Where the function continues to call itself.
-
Direct Recursion: Function calls itself directly.
-
Indirect Recursion: A function calls another function that ultimately calls the first.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
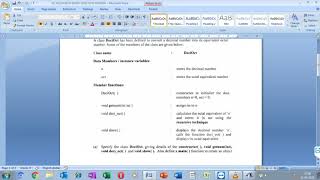
Calculating the factorial of a number using recursion.
-
Calculating Fibonacci numbers through recursive calls.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
π΅ Rhymes Time
-
Recursion, it's true, helps break problems in two. With base cases to stop, and recursive calls on top.
π Fascinating Stories
-
Imagine a wise wizard who continuously shrinks down a big task into little bits until he finds just the right size to solve, helping him tackle even the most colossal challenges.
π§ Other Memory Gems
-
BRR: Base case, Recursive case, Repeat!
π― Super Acronyms
BRB - Base case, Recursive function, Box (to remember the stack structure).
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Recursion
Definition:
A programming technique where a function calls itself to solve problems by breaking them down into smaller sub-problems.
-
Term: Base Case
Definition:
The condition that terminates the recursion process, preventing infinite loops.
-
Term: Recursive Case
Definition:
The part of the function where the function calls itself with modified parameters.
-
Term: Stack Overflow
Definition:
An error that occurs when too many nested recursive calls exceed the call stack memory limit.
2. Recursive Case
The part of the function where the function calls itself with modified arguments, moving towards the base case.
- Detailed Explanation: Every recursive function must have two essential parts: the base case and the recursive case. The base case determines the condition under which the recursion should end. Without this base case, the function would keep calling itself endlessly, leading to an error known as stack overflow. The recursive case, on the other hand, is the part where the function does its work to get closer to the base case. It adjusts the parameters with each call to ensure that eventually, the base case will be reached.
- Real-Life Example or Analogy: Think of climbing down a staircase. The base case is reaching the bottom step where you stop. The recursive case is taking each step down one by one until you reach that last step. If you forget where the last step is, you might keep going down endlessly.
- Chunk Title: How Recursion Works
- Chunk Text: When a recursive function is called, the computer stores each function callβs parameters and local variables in a call stack until the base case is reached. Then, the functions return their values one by one in reverse order (stack unwinding).
- Detailed Explanation: Recursion functions use a structure known as the call stack to manage function calls. Each time a function is called, its data is placed on the top of the stack. As functions reach their base cases, they start to return values, popping off the stack until control returns to the initial caller. This process is called stack unwinding. It ensures that values are computed correctly by resolving them in the opposite order of the function calls.
- Real-Life Example or Analogy: Imagine you are stacking plates. Each plate represents a function call. When you stack them up, you keep adding plates (calls). To get to the bottom plate, you must remove the top plates first. As you remove them, you uncover the one at the bottom, just like how functions resolve their values as they return from each call.
- Chunk Title: Types of Recursion
- Chunk Text: ### 1. Direct Recursion:
A function calls itself directly.
2. Indirect Recursion
A function calls another function which eventually calls the first function.
- Detailed Explanation: Recursion can be categorized into two main types: direct and indirect. In direct recursion, a function directly calls itself to solve a problem. In contrast, indirect recursion occurs when one function calls another function, which ultimately results in a call back to the original function. Understanding these distinctions helps in identifying and analyzing recursive patterns in programming.
- Real-Life Example or Analogy: Think of a pair of friends relaying a message. In direct recursion, one friend tells the other to pass the message directly back to herself. In indirect recursion, friend A tells friend B to relay the message to friend C, who then tells friend A. Both methods can reach the same conclusion, but through different pathways.
- Chunk Title: Examples of Recursion
- Chunk Text: #### 1. Factorial of a Number
The factorial of a non-negative integer n is defined as: - π! = πΓ(πβ1)Γ(πβ2)Γβ―Γ1
- 0! = 1 (by definition)
Recursive definition:
- Base case: 0! = 1
- Recursive case: π! = πΓ(πβ 1)!
Python code example:
Example usage
print(sum_of_digits(1234)) # Output: 10
2. Fibonacci Series
The Fibonacci sequence is a series of numbers where the next number is the sum of the previous two:
- πΉ = 0
- πΉ = 1
- πΉ = πΉ + πΉ for π β₯ 2
Python code example: