Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skillsβperfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
Youβve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take mock test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Motion
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Welcome everyone! Today we're diving into the concept of motion. Motion is defined as the change in position of a body relative to a time frame and a reference point.
What types of motion are there, sir?
Great question! There are three main typesβtranslatory, rotational, and vibratory. In this chapter, we'll focus on translatory motion, which can either be linear or curved.
Could you explain what translatory motion is?
Sure! Translatory motion refers to movement along a straight line or a curve. An example is a car driving down a straight road.
Isn't rotational motion when something spins around, like a wheel?
Exactly! In rotational motion, an object moves around a fixed axis. Any questions so far?
No, this is clear. What's our next topic?
Next, weβll discuss important terms in motion.
Important Terms in Motion
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Letβs explore some important terms such as distance, displacement, speed, velocity, and acceleration. Distance is the total path length travelled, while displacement is the shortest distance between two points.
So, distance is always positive, right?
Correct! Displacement, however, can be positive, negative, or zero, depending on the direction of movement.
What about speed and velocity, sir?
Speed is a scalar quantity measuring how fast something movesβit's just distance over time. Velocity, on the other hand, is a vector quantity indicating speed in a specific direction.
Can you give us the formulas for speed and velocity?
Of course! Speed is calculated as `Speed = Distance/Time`, and velocity is `Velocity = Displacement/Time`. Let's remember these formulas using the acronym SVD: Speed = Distance over Time & Velocity = Displacement over Time.
This is beginning to make sense!
Acceleration
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now, let's talk about acceleration! It's defined as the rate of change of velocity over time.
What is the formula for acceleration?
The formula is `Acceleration (a) = Change in velocity/Time taken`, or `a = (v - u)/t`, where 'u' is the initial velocity, 'v' is the final velocity, and 't' represents time.
What does positive and negative acceleration mean?
Positive acceleration means the object is speeding up, while negative acceleration, or deceleration, means itβs slowing down. How about real-life examples? If a car accelerates when the light turns green, that's positive acceleration!
What if the car is slowing down to stop?
That's negative acceleration! Now, can anyone summarize what we've learned about acceleration?
Equations of Motion
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
As we dive into equations of motion, there are three crucial formulas for uniformly accelerated motion: `v = u + at`, `s = ut + 1/2 atΒ²`, and `vΒ² = uΒ² + 2as`.
What do these symbols stand for?
Good question! Here, 's' is displacement, 'u' is initial velocity, 'v' is final velocity, 'a' is acceleration, and 't' is time. It's important to know how to apply these equations!
Can you give us a scenario where we might use these equations?
Certainly! If you want to calculate how far a car travels while it accelerates from rest to a certain speed over a specific time, these equations will help you determine that.
So, it relates to real-world physics!
Absolutely! Understanding these equations allows us to connect the dots between theory and real-life applications. Now, who can give a brief recap of the equations?
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section explores the fundamentals of motion in one dimension, detailing definitions and differences between distance and displacement, as well as introducing concepts of speed, velocity, and acceleration. It provides key equations for uniformly accelerated motion and discusses graphical representations of motion.
Detailed
Detailed Summary
In this chapter, we delve into the concept of motion in one dimension, a fundamental aspect of physics that deals with the change in position of an object over time relative to a reference point.
Key Concepts:
- Types of Motion: We primarily focus on linear or translatory motion, which can either be in a straight line or along a curved path. Other types include rotational and vibratory motion.
- Important Terms: Understanding distance and displacement is crucial:
- Distance is the total path length travelled, while displacement measures the shortest distance from the initial to the final point.
-
Speed and velocity are key in describing motion:
- Speed is the rate of change of distance, presented as a scalar, whereas velocity is the rate of change of displacement and serves as a vector quantity.
- The concept of acceleration represents the rate of change of velocity.
- Distance vs. Displacement: Distance, being scalar, can only have positive values, while displacement, as a vector, can be positive, negative, or zero depending on the position of the object.
- Speed and Velocity: We differentiate between uniform, variable, average speeds, and their corresponding velocities using formulas, leading to equations of uniformly accelerated motion:
- Speed Formula:
Speed = Distance/Time -
Velocity Formula:
Velocity = Displacement/Time -
Acceleration: Positive acceleration indicates speeding up, while negative signifies deceleration. The relationship is established through the formula:
Acceleration (a) = Change in velocity/Time taken. - Graphical Representation: The section illustrates how distance-time and velocity-time graphs can represent motion, with specific attention on slopes and areas under the curves.
- Equations of Motion: The chapter culminates with essential equations used in uniformly accelerated motion, which are critical for solving many physics problems related to motion in one dimension.
The discussion also includes free fall and acceleration due to gravity, bridging theory with practical understanding.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Motion
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Motion is the change in position of a body with respect to time and a reference point.
Detailed Explanation
Motion refers to the change in the position of an object as time passes. To understand motion, it's important to reference a point, known as a reference point, which helps to determine if an object is moving or stationary. For example, when you are on a moving bus, everything outside the bus is your reference point, and how the bus changes its position regarding that reference is what we describe as motion.
Examples & Analogies
Imagine you are watching a train pass. The trees and buildings outside remain stationary, while the train moves from one point to another. This illustrates motion with respect to a stationary background.
Types of Motion
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
β Translatory motion: Linear movement (straight line or curve) β Rotational motion: About a fixed axis β Vibratory motion: To and fro about a mean position
Detailed Explanation
There are various types of motion which can be classified as follows:
1. Translatory motion refers to the movement along a straight path or a curve, like a car driving on a road.
2. Rotational motion involves objects turning around a fixed point or axis, like the Earth rotating around its axis.
3. Vibratory motion consists of back-and-forth movements around a central point, such as a pendulum swinging in a clock.
Examples & Analogies
Think of a merry-go-round. As it spins, riders experience rotational motion. When swinging on a swing, your motion is vibratory, moving back and forth from a central position.
Important Terms
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Quantity Description SI Unit
Distance Total path length travelled Metre (m)
Displacement Shortest distance from initial to final point Metre (m)
Speed Rate of change of distance m/s or km/h
Velocity Rate of change of displacement m/s or km/h
Acceleration Rate of change of velocity m/sΒ²
Detailed Explanation
This section defines essential terms associated with motion.
- Distance is the total length of the path traveled by an object, always a positive quantity measured in meters.
- Displacement is the straight line distance from the starting point to the endpoint and can be positive, negative, or zero depending on direction.
- Speed is how fast an object moves and is calculated as the distance traveled over time, measured in meters per second (m/s) or kilometers per hour (km/h).
- Velocity, similar to speed, also considers direction and is the displacement over time.
- Acceleration measures how quickly an objectβs velocity changes and is expressed as meters per second squared (m/sΒ²).
Examples & Analogies
If you drive 3 km east and then 4 km west, your distance is 7 km, but your displacement is 1 km west. If you take ten seconds to cover that distance, your speed is 0.7 km/h, while the velocity accounts for the direction and could be negative if we define east as positive.
Distance vs. Displacement
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Feature Distance Displacement
Scalar/Vecto Scalar Vector
r Value Always positive Can be positive, negative, or zero
Path Actual path Shortest path
Detailed Explanation
This comparison distinguishes distance from displacement.
- Distance is a scalar quantity, meaning it only has magnitude and is always positive.
- Displacement, by contrast, is a vector quantity, which includes both magnitude and direction and can be positive, negative, or zero depending on the objectβs motion.
- Also, distance refers to the actual path taken, while displacement refers to the shortest path between two points.
Examples & Analogies
Consider a situation in a park where you walk around a pond taking 100 meters of path. Your distance is 100 meters. However, if the pond was 30 meters across, your displacement (straight line from start to end) would only be 30 meters, showcasing the difference between these two concepts.
Speed and Velocity
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Speed = Distance travelled / Time taken
Velocity = Displacement / Time taken
β Uniform speed/velocity: Same magnitude at all times
β Variable speed/velocity: Changes with time
β Average speed = Total distance / Total time
Average velocity = Total displacement / Total time
Detailed Explanation
In understanding speed and velocity:
- Speed is the total distance an object travels divided by the time it takes, while velocity includes directional information and is the ratio of displacement over time.
- If a car travels at the same speed throughout its journey, it has uniform speed, whereas if it speeds up or slows down, it has variable speed.
- Average speed and average velocity provide a general idea of motion over a journey by totaling the distances or displacements covered during the total time of travel.
Examples & Analogies
Imagine driving to a friend's house. Initially, you might go slowly in traffic (low speed) and then speed up on a highway (high speed). Your overall average speed helps determine how long the trip took, but velocity reflects how quickly you reached your destination directly.
Acceleration
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Acceleration (a) = Change in velocity / Time taken = (v - u) / t
Where: β u = initial velocity β v = final velocity β t = time taken
β Positive acceleration β speeding up
β Negative acceleration (deceleration) β slowing down
Detailed Explanation
Acceleration describes how quickly an object's velocity changes over time. Its formula indicates the difference between final velocity (v) and initial velocity (u) divided by the time (t) taken.
- If an object speeds up, it has positive acceleration.
- Conversely, if it slows down, it experiences negative acceleration, often called deceleration.
Examples & Analogies
Picture a bicycle racer. As the biker pedals harder going downhill, their speed increases, demonstrating positive acceleration. However, when they tap the brakes to slow down at a turn, that's an example of negative acceleration.
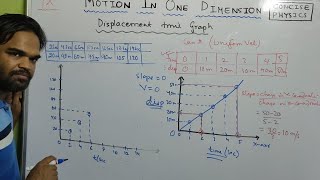
Graphical Representation of Motion
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
- Distance-Time Graph
β Uniform motion: Straight line with constant slope
β Non-uniform motion: Curved line - Velocity-Time Graph
β Uniform acceleration: Straight sloping line
β Area under graph = distance travelled
β Slope = acceleration
Detailed Explanation
Graphical representations help visualize motion:
1. Distance-Time Graphs show how distance changes over time. Straight lines indicate uniform motion, while curved lines imply changing speeds.
2. Velocity-Time Graphs depict how velocity varies with time. A straight line suggests uniform acceleration, and the area beneath the line represents the total distance traveled while acceleration represents the slope of the line.
Examples & Analogies
Imagine a race track; a distance-time graph for a runner might show them moving steadily (straight line). If they sprint (acceleration), the graph curves upwards. Conversely, in a velocity-time graph indicating acceleration, the steeper the line goes up, the faster the runner is gaining speed.
Equations of Uniformly Accelerated Motion
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
- v = u + at
- s = ut + 1/2 atΒ²
- vΒ² = uΒ² + 2as
Where: β s = displacement β u = initial velocity β v = final velocity β a = acceleration β t = time taken
Detailed Explanation
These equations relate initial velocity (u), final velocity (v), acceleration (a), time (t), and displacement (s) in uniformly accelerated motion.
1. The first equation calculates the final velocity after a specific time based on initial velocity and acceleration.
2. The second equation helps determine displacement over time given initial velocity and acceleration.
3. The third enables the calculation of final velocity based on displacement and acceleration.
Examples & Analogies
Think of a car speeding up from a standstill. Using these equations, you can calculate how fast it will be going after a given time or how far it will travel under constant acceleration.
Free Fall and Acceleration due to Gravity
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
β Free fall: Motion of an object under gravity alone.
β Acceleration due to gravity (g): g β 9.8 m/sΒ²
β In free fall: a = g, u = 0
β Equations used: v = gt, s = 1/2 gtΒ², vΒ² = 2gs
Detailed Explanation
Free fall describes how objects fall toward the Earth solely due to the pull of gravity, with no air resistance affecting them. The acceleration due to gravity is approximately 9.8 m/sΒ². When an object falls without any initial velocity, its motion is described using formulas that show how its speed and distance change over time.
Examples & Analogies
Consider dropping a ball from a height. Without any external forces, it will accelerate downwards at 9.8 m/sΒ² due to gravity. You can use the mentioned equations to predict how fast the ball will be traveling just before hitting the ground and how far it will fall in a given time.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Types of Motion: We primarily focus on linear or translatory motion, which can either be in a straight line or along a curved path. Other types include rotational and vibratory motion.
-
Important Terms: Understanding distance and displacement is crucial:
-
Distance is the total path length travelled, while displacement measures the shortest distance from the initial to the final point.
-
Speed and velocity are key in describing motion:
-
Speed is the rate of change of distance, presented as a scalar, whereas velocity is the rate of change of displacement and serves as a vector quantity.
-
The concept of acceleration represents the rate of change of velocity.
-
Distance vs. Displacement: Distance, being scalar, can only have positive values, while displacement, as a vector, can be positive, negative, or zero depending on the position of the object.
-
Speed and Velocity: We differentiate between uniform, variable, average speeds, and their corresponding velocities using formulas, leading to equations of uniformly accelerated motion:
-
Speed Formula:
Speed = Distance/Time -
Velocity Formula:
Velocity = Displacement/Time -
Acceleration: Positive acceleration indicates speeding up, while negative signifies deceleration. The relationship is established through the formula:
Acceleration (a) = Change in velocity/Time taken. -
Graphical Representation: The section illustrates how distance-time and velocity-time graphs can represent motion, with specific attention on slopes and areas under the curves.
-
Equations of Motion: The chapter culminates with essential equations used in uniformly accelerated motion, which are critical for solving many physics problems related to motion in one dimension.
-
The discussion also includes free fall and acceleration due to gravity, bridging theory with practical understanding.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
If a car travels 100 meters in 10 seconds, its speed is 10 m/s.
-
If a person walks 300 meters northeast in a straight line, their displacement is 300 meters to the northeast.
-
An object drops from a height experiencing free fall will have an acceleration of approximately 9.8 m/sΒ² due to gravity.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
π΅ Rhymes Time
-
To move in a line, that's motion divine; distance is straight, while displacement's not late!
π Fascinating Stories
-
Imagine a race car speeding down a track. It covers many twists and turns, representing distance, but its quickest route to the finish line represents displacement!
π§ Other Memory Gems
-
To remember the order of motion equations, use 'Vaccine Statements'. - v = u + at, s = ut + 1/2 atΒ², vΒ² = uΒ² + 2as.
π― Super Acronyms
D.V.S.A - Distance, Velocity, Speed, Acceleration!
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Motion
Definition:
The change in position of an object with respect to time.
-
Term: Distance
Definition:
Total path length travelled by an object.
-
Term: Displacement
Definition:
Shortest distance from initial to final point, with direction considered.
-
Term: Speed
Definition:
Rate of change of distance travelled (scalar).
-
Term: Velocity
Definition:
Rate of change of displacement (vector).
-
Term: Acceleration
Definition:
Rate of change of velocity over time.
-
Term: Uniform Motion
Definition:
Motion at a constant speed in a straight line.
-
Term: Nonuniform Motion
Definition:
Motion with varying speed.