Speed and Velocity
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Defining Speed and Its Calculation
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Good morning everyone! Today, we will discuss speed. Can anyone tell me what speed means?

Is it how fast something moves?

Exactly! Speed measures how fast an object is moving. We calculate it using the formula: Speed = Distance travelled divided by Time taken. This means, if you know how far an object has gone and how long it took, you can find its speed.

So if I run 100 meters in 10 seconds, my speed is 10 meters per second?

That's correct, Student_2! Remember this formula: Speed = Distance/Time. Let's remember it with the acronym ST: S for Speed, T for Time, and D for Distance.

What if I run slower or faster during my run? Does that change my speed?

Great question! The speed can vary if you're not moving at a constant pace, so we will discuss variable speed next.

What if we average it over the whole distance?

Good point! To find average speed, we use Average Speed = Total Distance divided by Total Time. Let’s wrap up this session by remembering: Speed is a scalar quantity, meaning it only has magnitude.
Understanding Velocity and Its Calculation
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now, let's transition to velocity. How is it different from speed?

I think velocity includes direction?

Exactly! Velocity is a vector quantity, meaning it has both magnitude and direction. The formula is similar: Velocity = Displacement / Time taken. It’s important to note that displacement is the shortest path from the initial to the final point.

So, if I walk back to where I started, my displacement is zero?

Yes! And thus, your average velocity would also be zero since there’s no change in your position. To help remember, think of the term 'vector' pointing in a specific way; we could use the mnemonic 'D over T' as a reminder for Displacement over Time.

How does that relate to speed again?

Good question! While speed only measures how fast something moves, velocity gives the direction of that movement. This is crucial in navigation and physics where direction matters.

Can velocity ever be negative?

Yes, if an object moves backward from its original position, its velocity can be negative. Remember, velocity can be positive, negative, or even zero, depending on the direction of displacement.
Uniform vs. Variable Speed and Velocity
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Let’s talk about uniform and variable speed. What do you think uniform speed means?

I think it means going at the same speed the whole time.

Right! Uniform speed means that the speed remains constant over time. In contrast, variable speed means it changes. Think about when you ride a bike and speed up or slow down.

So velocity can also be uniform or variable then?

Absolutely! Uniform velocity entails moving at a constant speed in a straight line, while variable velocity involves changes in speed or direction. Let’s keep these terms in mind using this mnemonic: U for Uniform -> Always the same!

Can I get an example of variable speed?

Consider a car that accelerates from a stoplight and then slows down at a traffic jam; that's variable speed at work! To summarize, speed focuses on how fast and velocity incorporates direction.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
This section defines speed and velocity, illustrating their calculations and differences. It discusses uniform and variable rates, along with the formulations for average speed and average velocity, providing clear distinctions between these two essential concepts in motion.
Detailed
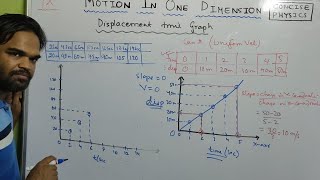
In this section, we explore the concepts of speed and velocity, both critical in understanding motion. Speed is calculated by the formula: Speed = Distance travelled / Time taken, primarily focusing on how fast an object moves irrespective of direction. In contrast, velocity, defined as the rate of change of displacement, is expressed as Velocity = Displacement / Time taken, factoring in direction. We categorize speed and velocity into uniform (constant) and variable (changing) states and discuss average speed, calculated as Average Speed = Total distance / Total time, and average velocity as Average Velocity = Total displacement / Total time. Recognizing these distinctions is crucial for physics studies and real-world applications.
Youtube Videos









Audio Book
Dive deep into the subject with an immersive audiobook experience.
Definition of Speed
Chapter 1 of 3
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Speed = Distance travelled / Time taken
Detailed Explanation
Speed is a measure of how fast an object is moving, defined as the total distance traveled divided by the time taken to cover that distance. It indicates the rate at which distance is covered and is generally measured in units of meters per second (m/s) or kilometers per hour (km/h). Thus, if a car travels 100 meters in 5 seconds, its speed would be 20 m/s, calculated by dividing 100 m by 5 s.
Examples & Analogies
Imagine you're running a race. If you complete a 400-meter lap in 50 seconds, you can calculate your speed. This can help you understand your performance, just like a driver checks the speedometer to see how fast they are going on the road.
Definition of Velocity
Chapter 2 of 3
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Velocity = Displacement / Time taken
Detailed Explanation
Velocity is similar to speed, but with an important difference: it is defined as the rate of change of displacement over time. Displacement takes into account not just the distance traveled but also the direction of motion. Thus, if an object moves from point A to point B (10 meters to the east) in 2 seconds, its velocity would be 5 m/s to the east. This shows both how fast the object is moving and the direction in which it is moving.
Examples & Analogies
Consider driving from your home to a friend's house in the north direction. Regardless of how many twists and turns you take on the way, your displacement is the straight-line distance from your home to your friend's house. This illustrates that velocity gives a complete picture when combined with direction, which is crucial for navigation.
Types of Speed and Velocity
Chapter 3 of 3
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
● Uniform speed/velocity: Same magnitude at all times
● Variable speed/velocity: Changes with time
● Average speed/velocity:
- Average Speed = Total distance / Total time
- Average Velocity = Total displacement / Total time
Detailed Explanation
Speed and velocity can be classified into different types. Uniform speed means an object is moving at a constant speed, such as a car cruising at a steady 60 km/h on a highway. Variable speed indicates that the speed changes, like a car accelerating or decelerating in traffic. Average speed is the total distance divided by the total time taken for a trip. Meanwhile, average velocity also considers the direction, defined as the total displacement divided by the total time, which can be quite different from average speed if the route is not straight.
Examples & Analogies
Think of a runner racing in a circular track. If they complete one round at the same pace, their speed is uniform. However, if they speed up or slow down at different parts of the track (like starting strong and losing pace on a curve), they have variable speed. At the end, if we consider their total distance and net displacement (which might be zero if they finished where they started), average speed and average velocity will give two different measures of their performance.
Key Concepts
-
Speed: The rate of distance traveled regardless of direction.
-
Velocity: The rate of change of displacement with direction.
-
Uniform Speed/Velocity: Constant rate of change.
-
Variable Speed/Velocity: Changing rate of change.
-
Average Speed/Velocity: Computed over the entire distance and time.
Examples & Applications
A runner finishes a 400m track in 50 seconds. Speed = 400m / 50s = 8 m/s.
If a car moves 120 km north in 2 hours, its average velocity = 120 km / 2h = 60 km/h north.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
To find your speed, just remember the deed, Distance divided by Time is all you need!
Stories
Imagine a race where a car starts fast, keeps its speed, and finishes first. This illustrates uniform speed.
Memory Tools
D for Displacement, T for Time, in finding Velocity it’s truly sublime!
Acronyms
S for Speed, V for Velocity, E for Even pace, C for Changes in pace.
Flash Cards
Glossary
- Speed
The rate at which distance is covered, calculated as distance divided by time.
- Velocity
The rate of change of displacement, incorporating direction into its calculation.
- Displacement
The shortest distance from the initial to the final position of an object.
- Average Speed
Total distance travelled divided by total time taken.
- Average Velocity
Total displacement divided by total time taken.
Reference links
Supplementary resources to enhance your learning experience.
