Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Concept of Diagonalization
Unlock Audio Lesson
Today, we're going to learn about diagonalization. A matrix A is diagonalizable if it's similar to a diagonal matrix D, meaning we can write it as D = P^{-1}AP. Can anyone tell me why this might be important?
I think it makes calculations easier, right?
Exactly! Diagonalization simplifies many operations, particularly when we need to compute powers of the matrix. Does anyone know what P represents?
Isn't it the matrix whose columns are the eigenvectors of A?
Correct! P contains the linearly independent eigenvectors. Let's remember: *D for Diagonal and P for eigenvectors*. Anyone knows the primary condition for a matrix to be diagonalizable?
A needs to have n linearly independent eigenvectors.
Right! Great job! This is pivotal for our next lesson. In summary, diagonalization helps us significantly in computational efficiency.
Conditions for Diagonalization
Unlock Audio Lesson
Now let’s dive deeper into the conditions for diagonalization. Can anyone suggest when a matrix is guaranteed to be diagonalizable?
If it has n distinct eigenvalues?
Yes! Distinct eigenvalues ensure linear independence. What about symmetric matrices? Why are they special?
Symmetric matrices are always diagonalizable, right?
Absolutely! That characteristic is important in fields like civil engineering because symmetric matrices commonly represent stress or strain tensors. Remember: *Symmetric = Diagonalizable*.
So if a matrix has distinct eigenvalues or is symmetric, we can always diagonalize it?
That’s right! Let's recap. A matrix is diagonalizable if it has enough linearly independent eigenvectors, particularly n distinct eigenvalues or is symmetric.
Applications of Diagonalization
Unlock Audio Lesson
What do you think are some practical applications of diagonalization?
It could be used in solving differential equations?
Exactly! When we diagonalize a coefficient matrix in systems of linear differential equations, it simplifies the solution process. Can anyone think of other applications?
Like in dynamic systems or simulations?
Yes! Dynamic simulations, especially in civil engineering, where we predict how structures will respond, greatly benefit from diagonalization. To summarize, diagonalization is vital for efficient computations, system response analysis, and solving complex equations.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In this section, we explore the concept of diagonalization, where a matrix is transformed into a diagonal form if it is similar to a diagonal matrix. The conditions for diagonalizability are discussed, including the requirement for linearly independent eigenvectors, and its implications for computational efficiency in solving linear equations.
Detailed
Diagonalization and Similarity
In linear algebra, a matrix A is said to be diagonalizable if it can be expressed in the form $D = P^{-1}AP$, where D is a diagonal matrix consisting of the eigenvalues of A and P is a matrix whose columns are the corresponding linearly independent eigenvectors of A. Through diagonalization, one can simplify many matrix operations, such as raising matrices to powers and solving systems of linear equations, making it an essential concept in diverse applications including civil engineering.
Conditions for Diagonalizability
A matrix A is diagonalizable if and only if it has n linearly independent eigenvectors. This condition is always satisfied when:
- A has n distinct eigenvalues,
- A is symmetric, which has significant relevance in applications, particularly in civil engineering where symmetric matrices often arise in stress and strain calculations.
Diagonalization allows for simplification of computations, especially when dealing with dynamic systems. The expression $A^k = PD^kP^{-1}$ can be employed to compute high powers of A efficiently.
Significance
Understanding diagonalization is fundamental for addressing problems in eigenvalue analysis, stability, and system dynamics, making it a cornerstone concept in both theoretical and applied mathematics.
Youtube Videos
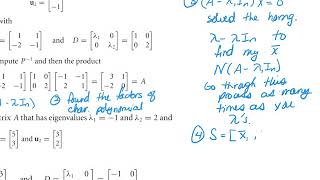
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Definition of Diagonalization
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
A matrix A is said to be diagonalizable if it is similar to a diagonal matrix D:
D = P⁻¹AP
Where D = diag(λ₁, λ₂, ..., λₙ), the eigenvalues of A, and P is the matrix whose columns are the linearly independent eigenvectors of A.
Detailed Explanation
A matrix is called diagonalizable if we can find a diagonal matrix that is similar to it. 'Similar' means there exists an invertible matrix P such that multiplying the matrix A by P and P's inverse leads us to the diagonal matrix D. The diagonal matrix D contains eigenvalues of A on its diagonal, which are special values that give us insight into the transformation properties of A. The columns of P are the corresponding eigenvectors of A, which are the vectors that do not change direction when the transformation is applied.
Examples & Analogies
Think of diagonalization like changing a complex machine into a simpler form that is easier to understand. Just as a complicated device might be broken down into its main components (which in this case, are the eigenvalues and eigenvectors), a matrix can be transformed into a simpler diagonal form while preserving essential information about its operation.
Conditions for Diagonalizability
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Matrix A is diagonalizable if and only if it has n linearly independent eigenvectors.
This is always true if:
– A has n distinct eigenvalues, or
– A is symmetric (especially relevant in civil engineering applications).
Detailed Explanation
For a matrix to be diagonalizable, it must have a number of unique eigenvectors equal to its size n. If a matrix has n distinct eigenvalues, it guarantees that the eigenvectors corresponding to those values will also be independent, thus ensuring diagonalizability. Furthermore, symmetric matrices (which are equal to their own transpose) have special properties that often ensure they can be diagonalized, leading to simplification in many engineering calculations.
Examples & Analogies
Imagine a classroom where each student has a unique skill (like a different eigenvalue). If every student can work independently on a project (having independent eigenvectors), the team can integrate their unique strengths into a single cohesive result. Conversely, if many students share the same skill, they may struggle to contribute uniquely, akin to matrices that don’t meet the diagonalizability conditions.
Implications of Diagonalization
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Diagonalization simplifies computation, especially when raising matrices to powers, as:
A^k = PD^kP⁻¹
This has implications in dynamic system simulations and solving systems of differential equations arising in civil structures.
Detailed Explanation
When a matrix A is diagonalized, computing powers of A becomes much easier. Instead of directly multiplying A by itself multiple times, we can take the diagonal matrix D, raise it to the k-th power easily (since powers of a diagonal matrix are simply the powers of the diagonal entries), and then use P and P's inverse to transform back. This efficiency greatly aids in simulations of dynamic systems, particularly in fields like civil engineering.
Examples & Analogies
Think of diagonalization as converting a complex recipe into simple, individual steps for each ingredient. Instead of mixing all at once (which is hard), you process each ingredient separately (D), which allows for quick adjustments and iterations (raising D to a power). Once each step is perfected, you blend them back together (using P and P⁻¹) to achieve your final dish – a more manageable approach in both cooking and matrix calculations!
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Diagonalization: A process of converting a matrix into a diagonal form.
-
Eigenvalues: Scalars indicating the factor by which eigenvectors are stretched during transformations.
-
Eigenvectors: Vectors that maintain their direction under linear transformations.
-
Similarity Transformation: A transformation that defines a relationship between two matrices that represent the same linear transformation.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Example 1: A matrix A is said to be diagonalizable if we can represent it as D = P^{-1}AP, with D being a diagonal matrix.
-
Example 2: If matrix A has distinct eigenvalues 4 and 3, it can be diagonalized efficiently.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Diagonalization's the key, when eigenvectors are free, compute with ease, your matrices, watch them like a breeze!
📖 Fascinating Stories
-
Imagine a magician turning a complex shape into a simple square. This is like diagonalization, simplifying matrices into diagonal forms with magic eigenvalues and vectors!
🧠 Other Memory Gems
-
D.E.S.I.G.N: Diagonalization = Eigenvalues, Symmetric = Independent, Good to go for calculations, Number of eigenvectors.
🎯 Super Acronyms
P.E.D.
- P: for eigenvectors
- E: for eigenvalues
- D: for diagonalized form.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Diagonalizable
Definition:
A matrix is diagonalizable if it can be expressed as a diagonal matrix via similarity transformation.
-
Term: Eigenvalue
Definition:
A scalar associated with a linear transformation represented by the matrix that characterizes the behavior of eigenvectors.
-
Term: Eigenvector
Definition:
A non-zero vector that changes at most by a scalar factor when a linear transformation is applied.
-
Term: Similarity
Definition:
Two matrices A and B are similar if there exists an invertible matrix P such that B = P^{-1}AP.