Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to the Spectral Theorem
Unlock Audio Lesson
Today, let's delve into the Spectral Theorem, which states that real symmetric matrices can be orthogonally diagonalized. This theorem is pivotal in various applications. Can anyone explain what we understand by 'orthogonal diagonalization'?
I think it means we can express a matrix in a way that its eigenvalues are neatly arranged on a diagonal, using an orthogonal transformation.
Exactly! And orthogonal transformations preserve lengths and angles. This leads us to consider the implications in engineering, especially stress calculations. What do you think that means for us?
It sounds like using these transformations, we could simplify complex stress analysis by identifying principal stresses.
Right on point! Remember, symmetric matrices assure us that our eigenvalues are real, which is a critical aspect of our calculations. Can anyone relate this to a practical example?
In structural engineering, if we have a stress tensor, we can find the principal stresses through diagonalization.
That’s exactly it! Let's summarize: The Spectral Theorem allows us to diagonalize real symmetric matrices, which is vital in applications like yield design and modal analysis.
Properties of Orthogonal Matrices
Unlock Audio Lesson
Let’s discuss the properties of the orthogonal matrix Q involved in the diagonalization. What do we know about the columns of Q?
They should be orthogonal unit vectors, meaning they are perpendicular and have a norm of one.
Correct! This orthogonality is crucial as it preserves the geometric structure of our vectors. Why is that important in applications?
Because we need to maintain the integrity of angles and distances, especially when working with physical quantities.
Perfect! Thus, orthogonal transformations help ensure that as we transform stresses, we don’t distort physical interpretations.
Does that mean every real symmetric matrix can be diagonalized using this method?
Yes, and that’s a powerful insight! This theorem guarantees that any real symmetric matrix is diagonalizable through orthogonal similarity. Let’s reinforce these ideas with a practical situation in engineering.
Applications in Civil Engineering
Unlock Audio Lesson
Transitioning to application, who can summarize what we've discussed regarding principal stresses using orthogonal diagonalization?
We can find the principal stresses by determining the eigenvalues of the stress tensor matrix through orthogonal transformation.
Precisely! And these eigenvalues give us critical information about the maximum and minimum stresses experienced by the material. How would you utilize this in a practical scenario?
When designing beams, we could analyze how they would behave under varied loading. Knowing the principal stresses would influence our material selection.
Exactly! The ability to accurately determine stress states through orthogonal diagonalization impacts both safety and material effectiveness in structures.
This seems like it would be especially useful when working with complex load patterns on structures.
Absolutely! And thus, understanding the orthogonal diagonalization helps engineers create safer designs by simplifying complex stress analysis.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section discusses the Spectral Theorem, establishing that real symmetric matrices can be orthogonally diagonalized, thus providing tangible applications like principal stress calculations in civil engineering. It discusses the implications of this theorem in terms of real eigenvalues and diagonal matrix representation.
Detailed
Orthogonal Diagonalization of Symmetric Matrices
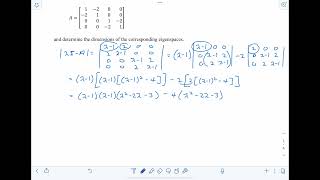
In this section, we explore the Spectral Theorem, which states that if A is a real symmetric matrix, it has real eigenvalues and can be orthogonally diagonalized. This means that there exists an orthogonal matrix Q such that:
$$ Q^T A Q = D $$
where D is diagonal. The significance of orthogonal diagonalization primarily lies in its applications in civil engineering, especially for calculating principal stresses and strains. Here, symmetry of matrices simplifies transformations to principal axes, ensuring that the resulting calculations preserve essential geometric properties like angle and length, which are crucial in structural analysis.
Youtube Videos
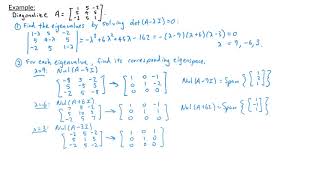
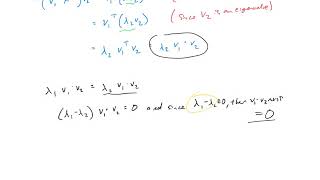
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Spectral Theorem Overview
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Theorem (Spectral Theorem): If A is a real symmetric matrix, then:
- All eigenvalues of A are real.
- There exists an orthogonal matrix Q such that:
Q^T A Q = D
where D is a diagonal matrix with eigenvalues of A on the diagonal.
Detailed Explanation
The Spectral Theorem states that for any real symmetric matrix A, its eigenvalues are always real numbers. This theorem guarantees that we can find an orthogonal matrix Q to transform A into a diagonal matrix D, where D contains the eigenvalues of A on its diagonal. The orthogonality of Q signifies that the transformation preserves angles and lengths, which is vital in many applications such as mechanics and structural analysis.
Examples & Analogies
Imagine a crystal structure where each atom's position can be defined using coordinates in 3D space. Transforming the coordinates so that the crystal aligns perfectly along its natural axes, without stretching or squishing the dimensions, is akin to the orthogonal diagonalization process. Just as the atomic positions rearrange into a simpler form that retains the original properties, the matrix simplifies to a diagonal form.
Real Eigenvalues
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
This is fundamental in:
- Principal stress/strain calculations.
- Transformation to principal axes in mechanics.
Detailed Explanation
The fact that all eigenvalues of a real symmetric matrix are real has practical implications in engineering and physics. For instance, in structural engineering, when calculating principal stresses or strains in materials, we need these values to be real for accurate assessments of stability and safety. The diagonalization ensures the system's response can be analyzed along principal axes, where the behavior is most predictable and simplified.
Examples & Analogies
Think of a bridge being tested for its stress levels. The stress on the bridge can be analyzed by measuring where the greatest forces act on it. By transforming the stress measurements (represented by a symmetric matrix) into a simpler form (diagonal), engineers can easily see the principal stresses, thus ensuring safety and efficacy in the bridge's design.
Application: Principal Stresses
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Given stress tensor:
\[ \sigma = \begin{bmatrix} \sigma_{xx} & \tau_{xy} \ \tau_{xy} & \sigma_{yy} \end{bmatrix} \]
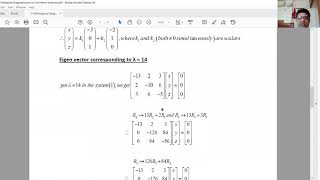
The principal stresses are the eigenvalues of this matrix, and the principal directions (angles) are given by eigenvectors. Since \( \sigma \) is symmetric, it can be orthogonally diagonalized.
Detailed Explanation
In the context of a stress tensor, we can represent the internal forces acting on a material as a 2x2 symmetric matrix. The diagonalization process helps us find the principal stresses (eigenvalues) and the angles at which these stresses occur (eigenvectors). This orthogonal diagonalization makes it much easier for engineers to determine where the material will experience maximum stress and strain.
Examples & Analogies
Consider a soft clay ball being pressed from different sides. As pressure is applied, it deforms in a predictable way, with certain directions experiencing more stress than others. By diagonalizing the stress tensor, engineers can simplify the analysis of how the clay will respond under various forces, just as they can find the most critical stress directions in any structural material.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Orthogonal Diagonalization: The process of transforming a symmetric matrix into diagonal form via orthogonal matrices, which do not alter distances.
-
Spectral Theorem: Establishes that every real symmetric matrix can be diagonalized, providing real eigenvalues essential for many applications.
-
Principal Axes: Directions in which a system experiences maximum and minimum stresses, found using eigenvalues and eigenvectors.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Given a symmetric stress tensor, diagonalization allows us to find principal stresses effectively through its eigenvalues.
-
Using the Spectral Theorem, we can transform a symmetric matrix representing a mechanical system into a diagonal form to simplify dynamic analysis.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Diagonalize with care and grace, symmetric matrices have their place.
📖 Fascinating Stories
-
Imagine a bridge being built; engineers use symmetric matrices to find where stress is felt the most. Via orthogonal diagonalization, they ensure that every beam bears weight in a balanced way without losing its strength.
🧠 Other Memory Gems
-
SPE - Symmetric, Principal, Eigenvalues: Remember these key terms for understanding orthogonal diagonalization.
🎯 Super Acronyms
SAD - Symmetric, And, Diagonalizable
- Highlighting the properties essential for using the Spectral Theorem.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Orthogonal Diagonalization
Definition:
The process of transforming a matrix into a diagonal form using an orthogonal transformation, preserving properties like angles and lengths.
-
Term: Spectral Theorem
Definition:
A theorem stating that every real symmetric matrix can be diagonalized by an orthogonal matrix.
-
Term: Symmetric Matrix
Definition:
A square matrix that is equal to its transpose, having real eigenvalues.
-
Term: Principal Stresses
Definition:
The maximum and minimum normal stresses at a point in a stressed body, indicated by the eigenvalues of the stress tensor.