Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Deflections
Unlock Audio Lesson
Welcome, class! Today we will discuss the importance of deflections in structures. Why do you think controlling deflection is critical in design?
Isn't it to ensure that the structures are safe for use?
Very good! Yes, deflections must be limited to meet serviceability requirements—typically to values like (1/360) of the span length. This ensures safety and comfort. Anyone know what that might look like in a practical example?
Maybe like in bridges or buildings where too much bending can cause problems?
Exactly! Let's remember the acronym S.A.F.E. for Serviceability, Acceptable, Flexibility, and Efficacy in our designs.
Flexural Deformation
Unlock Audio Lesson
Now let's dive deeper into flexural deformation. Can anyone explain what flexural deformation involves?
Isn't it how beams bend under load?
Correct! When a beam bends, we relate its slope and curvature through equations. For instance, the curvature (𝓚) is defined as the change in slope per unit length. Who remembers how we express these relationships mathematically?
Is it something like d𝓸/ds = 𝓚?
Yes! We'll illuminate this relationship further with our visual aids. Understanding these derivations helps visualize how structures respond to load.
Differential Equation of the Elastic Curve
Unlock Audio Lesson
Let’s discuss the differential equation of the elastic curve. Why is this important?
It helps in calculating deflections based on material properties, right?
Exactly! This equation connects curvature with deflection and moment. Remember the formula M = EI(d^2y/dx^2), where 'E' is the modulus of elasticity and 'I' is the moment of inertia. Why do these parameters matter?
They define how much the material can bend without failing?
Yes! Great point. Let's recap that as MEMORY—Material Properties, Elasticity, Moment, and Yield.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
This section discusses the necessity of determining deflections in structures to meet serviceability requirements, specifically focusing on flexural deformation. It also introduces the curvature equation and differential equations of the elastic curve as foundational concepts, setting the stage for further discussions of axial and torsional deformations, and paving the way for more advanced methods grounded in energy considerations.
Detailed
Detailed Summary
In this section, we delve into the topic of deflections in structures, which are crucial to ensure that they meet serviceability requirements. The focus is primarily on flexural deformation, characterized by the curvature of beams subjected to bending loads.
Key Concepts:
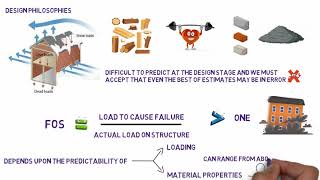
- Deflections: Must be limited under service loads to values such as (1/360) of the span length.
- Structure Analysis: Important for understanding statically indeterminate structures, ultimately highlighting the necessity for accurate deflection calculations.
- Flexural Deformation: Discusses the relationship between slope, curvature, and the radius of curvature within the context of flexural members.
Main Equations:
- The curvature equation relates slope and curvature to the y displacement through differential relationships.
- Differential Equation of the Elastic Curve: This fundamental relationship connects curvature with the elastic curve and linear strain. Additionally, it incorporates moment and curvature in structural analysis.
- Integrative approaches are utilized to derive moment equations and ultimately yield deflection equations through sequential integration.
Through this structured approach, various derivations lead to key implications about how structures respond to loading and, consequently, the practicality of ensuring comfort and safety in structural design.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Importance of Deflection Measurements
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Deflections of structures must be determined in order to satisfy serviceability requirements, i.e. limit deflections under service loads to acceptable values (such as L/360).
Detailed Explanation
Deflections are the displacements of structures caused by external forces. Measuring and controlling these deflections ensures that structures remain safe and comfortable for use. For example, a bridge must not bend too much under the weight of vehicles, as excessive bending can lead to structural failure or discomfort for users. The acceptable limit of deflection is often expressed as a ratio, such as L/360, meaning for every 360 units of length, the deflection should not exceed 1 unit.
Examples & Analogies
Think of a diving board. If you jump on the board, it will flex downwards. However, if it flexes too much, it could break or cause an uncomfortable experience for the diver. Similarly, buildings and bridges need to limit how much they flex to ensure safety and comfort.
Role of Deflection Calculations
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Later on, we will see that deflection calculations play an important role in the analysis of statically indeterminate structures.
Detailed Explanation
Statically indeterminate structures are those that cannot be analyzed using equilibrium equations alone. We need to consider additional factors, including deflections, to fully understand how these structures behave under loads. By calculating deflections, engineers can predict how structures will respond to various forces, leading to better design and safety.
Examples & Analogies
Imagine a team of engineers trying to understand how a multi-story building behaves when a strong wind blows. It's not just about how the building stays upright; they must also calculate how much it will sway or bend to ensure it remains stable and comfortable for occupants.
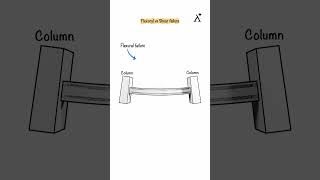
Focus on Flexural Deformation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
We shall focus on flexural deformation; however, by the end of this chapter, we will review axial and torsional deformations as well.
Detailed Explanation
Flexural deformation refers specifically to the bending of structural members under load. It is crucial to understand this type of deformation since it influences how beams, slabs, and other members behave when subjected to vertical loads. We will later expand our discussions to include axial deformation (lengthening or shortening of members) and torsional deformation (twisting of members). This comprehensive approach helps engineers consider all forms of deformation in their designs.
Examples & Analogies
Consider a ruler held at both ends and pressed down in the middle. It bends (flexural deformation). If you were to pull or push on its ends, it would stretch (axial deformation), and if you twisted one end, you would cause it to rotate (torsional deformation). Understanding these behaviors helps engineers design safer and more efficient structures.
Geometric Considerations of Deflection
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
This chapter will examine deflections of structures based on geometric considerations. Later on, we will present a more powerful method based on energy considerations.
Detailed Explanation
Geometric considerations involve analyzing the shapes and sizes of structural elements to determine how they will deflect under loads. The relationship between geometry and deflection is foundational in structural analysis, meaning that the way a structure is designed affects how it behaves when forces are applied. Energy methods, which we will explore later, take this a step further by analyzing how energy is distributed and transformed in a structure, allowing for a deeper understanding of its behavior.
Examples & Analogies
Think of an archway. Its curved shape allows it to hold a lot of weight without collapsing; this is a direct result of its geometry. If an archway were flat instead of curved, it would not bear loads as efficiently. Understanding these geometric relationships helps engineers design structures that can withstand forces effectively.
Curvature Equations and Definitions
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Let us consider a segment (between point 1 and point 2) of a beam subjected to flexural loading. The slope is denoted by θ, the change in slope per unit length is the curvature κ, and the radius of curvature is ρ. From Strength of Materials, we have the following relations: dθ/ds = 1/ρ, dθ = κ ds.
Detailed Explanation
In structural mechanics, when a beam bends, it creates angles (slope) and curves (curvature). The slope (θ) indicates how much the beam is tilting at any point, while curvature (κ) measures how sharply it is bending. The radius of curvature (ρ) provides a measure of this bend. These relationships help engineers calculate how much deflection occurs at various points along the beam when it is subjected to lateral loads.
Examples & Analogies
If you imagine bending a flexible straw, the angle at which you can push it down represents the slope, and the tightness of its curve represents the curvature. The easier it bends, the smaller the radius of curvature, while keeping it straight means a larger radius.
Relationships Between Slope, Curvature, and Displacement
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Thus the slope θ, curvature κ, and radius of curvature ρ are related to the y displacement at a point x along a flexural member by d²y/dx² = κ = 1/ρ.
Detailed Explanation
This equation shows a fundamental relationship in structural analysis: the second derivative of the vertical displacement (y) with respect to horizontal displacement (x) gives us the curvature of the beam. This means that if we know the shape of the beam and how it bends, we can determine how much it displaces vertically under load. This is crucial for ensuring the designed structures do not exceed allowable deflections.
Examples & Analogies
Think about a roller coaster track. The way it curves up and down (its shape) can be modeled mathematically, and knowing this allows engineers to predict how high the coaster will go or how fast it will drop, which is essential for both safety and thrill!
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Deflections: Must be limited under service loads to values such as (1/360) of the span length.
-
Structure Analysis: Important for understanding statically indeterminate structures, ultimately highlighting the necessity for accurate deflection calculations.
-
Flexural Deformation: Discusses the relationship between slope, curvature, and the radius of curvature within the context of flexural members.
-
Main Equations:
-
The curvature equation relates slope and curvature to the y displacement through differential relationships.
-
Differential Equation of the Elastic Curve: This fundamental relationship connects curvature with the elastic curve and linear strain. Additionally, it incorporates moment and curvature in structural analysis.
-
Integrative approaches are utilized to derive moment equations and ultimately yield deflection equations through sequential integration.
-
Through this structured approach, various derivations lead to key implications about how structures respond to loading and, consequently, the practicality of ensuring comfort and safety in structural design.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
A simply supported beam with a uniform load can be analyzed to determine its deflection using the equation δ = (5wL^4)/(384EI).
-
In a cantilever beam, the maximum deflection occurs at the free end, where δ = (wL^4)/(8EI) when a point load is applied.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Flex and bend, keep it nice; deflections should not pay a price.
📖 Fascinating Stories
-
Imagine a bridge that bends with the wind. It must not sway too much stay strong, and safe for all those who pass.
🧠 Other Memory Gems
-
M.E.D—Material, Elasticity, Deflection—three kings in the realm of bending.
🎯 Super Acronyms
S.A.F.E - Serviceability, Acceptable, Flexibility, and Efficacy in designs.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Deflection
Definition:
The displacement of a structural element under load.
-
Term: Curvature
Definition:
The measure of how much a curve deviates from being a straight line, specifically how steeply it bends.
-
Term: Elastic Curve
Definition:
The deflected shape of a beam under load, defining how it bends in response to applied forces.
-
Term: Moment of Inertia (I)
Definition:
A measure of an object's resistance to angular acceleration, dependent on the shape and distribution of mass.
-
Term: Modulus of Elasticity (E)
Definition:
A property that measures a material's ability to deform elastically when a force is applied.