Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Curvature Equation
Unlock Audio Lesson
Let's start by looking at the curvature equation. Can someone remind me how curvature relates to the curvature radius in a beam?
Curvature is defined as the reciprocal of the radius of curvature.
Exactly! So when we have bending, the curvature gives us insight into how sharply a beam is bending. Can anyone recall how we express that mathematically?
It’s formulated as \(\kappa = \frac{d^2y}{dx^2}\).
Good job! This means the curvature relates the second derivative of the deflection to curvature, which is vital when analyzing deflections.
So, curvature is directly tied to how much the beam deflects at a point?
Yes, and it leads us right into discussing the differential equation of the elastic curve.
In summary, curvature is key to understanding deflections in beams. It connects to how materials react under load, establishing relationships that are fundamental to structural design.
Relation between Moment and Curvature
Unlock Audio Lesson
Now let’s explore how the bending moment impacts curvature. The relationship is articulated in the equation: \(\frac{d^2y}{dx^2} = -\frac{M}{EI}\). Who can explain what each term represents?
\(M\) is the bending moment, \(E\) is the modulus of elasticity, and \(I\) is the moment of inertia.
Perfect! This shows that as the moment increases, the curvature increases, resulting in greater deflections. What implications does this have for structural integrity?
More bending could lead to larger deflections, possibly exceeding serviceability limits.
Correct! Hence, managing the bending moments is crucial in design to ensure beams do not sag excessively.
To summarize, the differential equation links moment and curvature, which is critical for assessing the behavior of structural elements under loading.
Practical Applications of the Elastic Curve Equation
Unlock Audio Lesson
Let’s discuss practical applications of the elastic curve equation in engineering design. Can anyone suggest a scenario where this might be critical?
In designing bridges, knowing how much the beam will deflect helps in ensuring safety and functionality.
Exactly! In bridge design especially, we need to make sure deflections remain below certain limits for comfort and safety.
So this equation helps engineers predict if the design is feasible?
Indeed! It forms the backbone of ensuring that structures will perform as expected throughout their lifespan.
To wrap up, the differential equation of the elastic curve is crucial for evaluating and designing safe structures, helping engineers understand how materials will behave under various loads.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In Section 8.1.2, we explore the differential equation of the elastic curve, emphasizing the relationships between curvature, deflection of beams, and moment in structural elements. This foundational concept aids in analyzing the behavior of beams under various loading conditions, significantly impacting structural design and serviceability.
Detailed
Differential Equation of the Elastic Curve
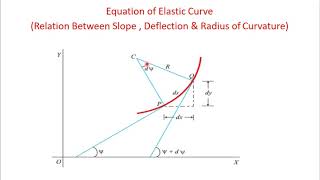
In this section, we define key relationships among curvature (denoted as \(\Theta\)), elastic curve (designated as \(y\)), and linear strain (represented as \(\epsilon\)). The elastic behavior of materials under load is critical for ensuring that structures meet serviceability requirements, such as limiting deflections to acceptable values.
Key Equations
- The slope of the curve is given by:\n\[
\frac{d\Theta}{ds} = \frac{1}{R},
\]
which indicates how the slope changes with respect to the arc length of the beam. - The curvature \(\kappa\) can be approximated for small deflections as:\n\[
\kappa = \frac{d^2y}{dx^2}.
\] - The fundamental relationship that ties all these concepts together under elastic loading is expressed by the equation:
\[
\frac{d^2y}{dx^2} = -\frac{M}{EI},
\]
where \(M\) represents the bending moment, \(E\) is the modulus of elasticity, and \(I\) is the moment of inertia of the beam's cross-section.
This differential equation is crucial in structural analysis, allowing engineers to calculate deflections of beams subjected to various loads and determine whether the structures can safely accommodate these deflections.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Basic Relationships of Elastic Curvature
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Again with reference to Figure 8.1 a positive d(θ) at a positive y (upper fibers) will cause a shortening of the upper fibers
\( \delta u = y \delta (\theta) \ (8.11) \)
Detailed Explanation
This equation describes the relationship between angular displacement (θ), which represents the rotation of the beam, and a corresponding change in length (δu) in the upper fibers of the beam. As the beam bends due to loading, the top fibers experience compressive strain, leading to a short length due to the curvature. This sets the foundation for understanding how displacement and strain are interconnected within the context of structural deformation.
Examples & Analogies
Imagine a rubber band. When you stretch it and then release one end, the top surface of the band will shorten as it curves, similar to how a beam's fibers shorten when loads are applied. The distance shortened on the top fibers represents the elastic response to bending, just like the rubber band reacting to your fingers pulling it.
Rewritten Relation of Strain and Displacement
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
This equation can be rewritten as
\(\lim_{\Delta s \rightarrow 0} \frac{\Delta u}{\Delta s} = y \lim_{\Delta s \rightarrow 0} \frac{\Delta \theta}{\Delta s} \ (8.12)\)
Detailed Explanation
This rewritten equation emphasizes that as the small segment length (Δs) approaches zero, the relationship between the change in vertical displacement (Δu) and the change in angular displacement (Δθ) also becomes more precise. It forms a foundational basis for deriving curvatures in beams where bespoken tensions and stresses are at play.
Examples & Analogies
Consider a soft ice cream cone. As you apply pressure on the top (the ice cream), the cone bends and the ice cream's shape changes slightly. The smaller you make the sections to measure the change in volume and shape, the more accurately you can describe the behavior of these changes. Like this, engineers analyze small segments of beams under load.
Combining Strain with the Curvature
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Combining this with Eq. 8.10 we obtain
\(\frac{d^2y}{dx^2} = -\frac{M}{EI} \ (8.16)\)
Detailed Explanation
This equation relates the second derivative of displacement (dy/dx) with the bending moment (M) acting on the beam and its stiffness characteristics denoted by EI (where E is the modulus of elasticity and I is the moment of inertia). Essentially, it states that the curvature of the elastic curve is directly proportional to the moment applied and inversely proportional to the stiffness of the beam, providing vital insights into how beams will respond to applied loads.
Examples & Analogies
Imagine bending a thick and rigid straw versus a thin and flexible one. The thicker straw will resist bending much more effectively than the thinner one, aligning with our understanding that the moment of inertia (I) and rigidity (EI) affect how structures bend under pressure. Construction engineers must understand these principles to design safer structures.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Curvature: A key concept representing how much a beam bends under a load, important for structural analysis.
-
Differential Equation: The relationship between moment, curvature, and deflection, crucial for predicting structural behavior.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
For a simply supported beam with a uniform load, the differential equation helps calculate the maximum deflection at the center using known load, span length, and material properties.
-
In reinforced concrete design, the elastic curve equation is used to ensure that beams meet the deflection criteria under both static and dynamic loads.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Bending beams like cypress trees, curvature grows with every squeeze.
📖 Fascinating Stories
-
Once there was a beam under a load, bending like a path on a solitary road. Its curvature was a tale of care, to ensure it didn’t fall, engineers were there.
🧠 Other Memory Gems
-
Remember CEM (Curvature, Elastic curve, Moment) to link the concepts!
🎯 Super Acronyms
MEL (Moment, Elastic curve, Load) for the key factors affecting deflection.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Curvature
Definition:
The amount by which a curve deviates from being a straight line; in this context, related to the bending of beams.
-
Term: Elastic Curve
Definition:
The deflected shape of a beam or structural element under loading.
-
Term: Strain (\(\epsilon\))
Definition:
The measure of deformation representing the displacement between particles in a material.
-
Term: Bending Moment (\(M\))
Definition:
A measure of the bending effect due to forces applied to a beam.
-
Term: Moment of Inertia (\(I\))
Definition:
A property of the cross-section of a beam that affects its resistance to bending.
-
Term: Modulus of Elasticity (\(E\))
Definition:
A material property indicating its stiffness; the ratio of stress to strain.