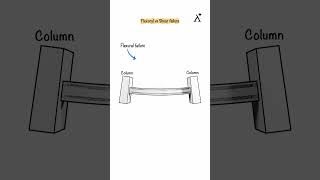
Flexural Deformations
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Flexural Deformations
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Welcome class! Today, we will explore flexural deformations, which are crucial for understanding how structures behave under load. Can anyone tell me why we care about deflections in structures?

It's important to ensure they don't bend too much, right?

Exactly! We typically limit deflections to prevent serviceability issues, like ensuring floors are comfortable to walk on. Does anyone know the common limit?

Is it 1/360 of the span length?

Correct! Now, let's dive deeper into the curvature equation and its significance.
Curvature and Displacement
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

When a beam bends, its curvature (κ) relates to the slope (θ) and displacement (y). Recall that for small angles, we can simplify equations. What does that tell us about our mathematical approach?

We can use simpler forms of the equations and still get accurate results?

Correct! Remember, for small displacements, the curvature can be approximated as d²y/dx². Why is this useful?

It helps us easily calculate deflections using basic calculus!

Exactly! Great understanding. Let's move to the differential equations of the elastic curve.
Differential Equations of the Elastic Curve
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now, we will examine how the moment (M) relates to curvature through the differential equations. Can someone give me the fundamental relationship we discussed?

It relates M = EI * d²y/dx²?

Exactly! Where EI represents the flexural rigidity. Why do you think this is important?

It shows how material properties affect the beam's responsiveness to bending.

Exactly! This underlines the dual role of curvature and material properties in predictable deflection outcomes.
Application of Moments to Flexural Deformations
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Let’s apply our newfound knowledge! Understanding how to derive the moment equation is essential for predicting deflection. Can anyone describe the steps?

We derive the moment equation from our curvature relationship and then integrate it to find displacement?

Right! Then, we apply boundary conditions to find constants of integration. What happens if the boundary conditions are not applied correctly?

We might get incorrect deflection values, leading to potential structural failures.

Exactly, well done everyone! This highlights the importance of precise application in engineering calculations.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
Flexural deformations are vital for understanding how structures deflect under loading. This section covers the relationships between curvature, displacement, and the effects of moments on beams, providing foundational concepts critical for future analyses of structures.
Detailed
Detailed Summary of Flexural Deformations
Flexural deformations describe how beams experience changes in shape when subjected to forces, leading to deflections critical for serviceability. This section emphasizes three core concepts:
- Curvature Equation: We establish relationships among slope (θ), curvature (κ), and radius of curvature (ρ) using differential equations. For small displacements, simplified equations relating these variables to beam displacement arise.
- Differential Equations of the Elastic Curve: The fundamental relationships between curvature, elastic curve, and strains are discussed. These relationships are independent of the material properties, encompassing both elastic and inelastic behavior.
- Application of Moments: The section concludes by examining how moments lead to calculations of flexural deformation through integrating moment equations. This interplay of geometry and mechanics is fundamental in ensuring structural integrity and performance.
Youtube Videos





Audio Book
Dive deep into the subject with an immersive audiobook experience.
Moment Equation
Chapter 1 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
- Moment Equation
\[
\frac{d^{2}y}{dx^{2}} \cdot EI = M = \frac{wL^{3}}{x} - \frac{5}{18}wL^{2}
\]
Detailed Explanation
This equation states that the second derivative of the displacement (y) with respect to the position (x) multiplied by the flexural rigidity (EI) equals the moment (M) at that section of the beam. This moment is influenced by the distributed load (w) and the geometry of the beam (L). The terms involved help understand how the bending of a beam responds to load.
Examples & Analogies
Imagine a diving board. When a person jumps on the diving board, their weight creates a bending moment. The equation helps show how much that moment impacts how much the board bends at each point. Just like bending a ruler gradually with your hands, it illustrates how forces lead to different responses along the length.
Integrate Once
Chapter 2 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
- Integrate once
\[
\frac{dy}{dx} = \frac{wL^{2}}{6}x^{2} - \frac{5}{18}x + C
\]
Detailed Explanation
This step updates our understanding by integrating the moment equation with respect to x once. This gives us the slope (dy/dx) as a function of x, which incorporates the effects of the load distributed across the beam. The constant (C) is determined using boundary conditions, indicating the slope at a certain point.
Examples & Analogies
Think about drawing a curve on a piece of paper. As you lift your pencil off the paper, the height of your pencil represents the slope of the curve at that point. Ultimately, knowing the slope at different points helps you understand the shape of the entire curve, helping illustrate how a beam bends under load.
Integrate Twice
Chapter 3 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
- Integrate twice
\[
EIy = \frac{wL^{2}}{18}x^{3} - \frac{wL^{2}}{36}x^{2} + C
\]
Detailed Explanation
This step continues from the previous one and integrates the slope equation once more to describe the overall deflection (y) of the beam under the applied load. The formula now relates the deflection directly to the applied load and its respective position along the beam. Boundary conditions at specific points (like where the beam is supported) are again applied to eliminate the constant.
Examples & Analogies
Think of a trampoline as an example of deflection. When someone jumps on the trampoline (applying a load), it deflects downwards. The formula helps us figure out just how much it will dip at various points depending on factors like weight and position on the trampoline, much like how we calculate deflection in the beam.
Boundary Conditions
Chapter 4 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Applying the boundary condition at x = 2L, we must have dy equal to the value coming from the left, thus C = 0.
Detailed Explanation
Boundary conditions are essential in ensuring our results are physically meaningful. By specifying conditions (like that the slope at certain endpoints should equal a specific value), we can solve for constants such as C that clarify the behavior of the beam under loading. Such constraints guide the calculations to reflect real-world scenarios.
Examples & Analogies
Think of boundary conditions like the rules of a game. They define how a player can move and score. In beam theory, these conditions similar to game rules tell you how the beam should respond at the ends based on the support conditions (like fixed or free), ensuring the calculations remain relevant and accurate.
Key Concepts
-
Curvature: A measure of how sharply a beam bends.
-
Deflection: The vertical displacement of a beam under load.
-
Elastic Curve: The graphical representation of the deflected shape of a beam.
-
Moment: The measure of force causing rotation around a point, crucial in beam deformation.
-
Flexural Rigidity: Represents a beam's ability to resist bending deformations.
Examples & Applications
When a beam is loaded at its center, it bends into an arc, illustrating curvature and resulting deflection.
A simply supported beam with known load and span can be analyzed using formulas to calculate expected deflection.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
When the beam bends low, it’s curvature we show, keep it in line, no deflection should flow.
Stories
Once, a builder placed a beam under heavy load. The beam bent, becoming a curvy path. They measured carefully, ensuring no deflection bothered the folks above!
Memory Tools
M-E-D-D: Moment, Energy, Deflection, Deformation - key concepts to remember.
Acronyms
CURV
Curvature
Uplift of load
Resulting deflection
Valid limits.
Flash Cards
Glossary
- Curvature
The measure of how much a curve deviates from being a straight line, defined mathematically as the derivative of the slope with respect to the displacement.
- Deflection
The degree to which a structural element is displaced under a load.
- Elastic Curve
The shape a beam takes under load, which can be described mathematically by differential equations relating deflection and moments.
- Moment
A measure of the rotational effect of a force, acting at a distance from a point.
- Flexural Rigidity
The product of a beam's modulus of elasticity and the moment of inertia, an indicator of a beam's resistance to bending.
Reference links
Supplementary resources to enhance your learning experience.
