Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Statically Indeterminate Structures
Unlock Audio Lesson
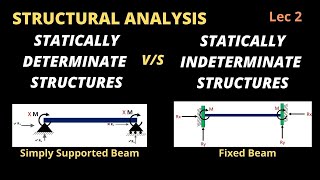
Today, we're discussing statically indeterminate structures. These structures have more unknowns than equations of equilibrium. Can anyone tell me why this might be significant?
It makes the analysis more complicated, right?
Exactly! This complexity arises because we must use additional methods to analyze them. Can anyone name some advantages of these structures?
They can handle failures without immediately collapsing, right?
Yes! That's an essential feature known as redundancy. It allows internal forces to redistribute in case of a failure in a support or member.
Requirements for Analysis
Unlock Audio Lesson
To analyze these structures, we need to satisfy three main requirements: equilibrium, force-displacement relations, and compatibility of displacements. Can anyone elaborate on what compatibility means in this context?
It means there shouldn't be any discontinuity in how the structure deforms under load?
Exactly! This ensures a stable and realistic behavior under applied loads. Now, how do we mathematically express these requirements?
I think we set up equations based on the forces and moments acting on the structure, right?
That's correct! It’s crucial to set up appropriate equations based on the load conditions.
Flexibility and Stiffness Methods
Unlock Audio Lesson
Now, let's dive into the analysis methods: the flexibility method and the stiffness method. Who can explain the flexibility method?
I think it focuses on the internal forces given certain displacements, right?
Yes, it relates to how a structure deforms under loading. And what about the stiffness method?
The stiffness method looks at displacements that result from known forces.
Exactly! Both methods serve as powerful tools, but they apply to different situations depending on what you know and what you need to find out.
Examples of Statically Indeterminate Structures
Unlock Audio Lesson
Let's discuss some examples of statically indeterminate structures. For instance, a cable-supported rigid plate. How many unknowns are involved in this system?
I think there are three unknowns for the forces in the cables, but only two equations of equilibrium.
Correct! This leads to a first-degree indeterminate scenario. Can anyone summarize why we need to consider material properties in these cases?
Because unlike determinate structures, the solution depends on the elastic properties of the materials!
Absolutely! You are catching on well, and it highlights the importance of understanding material behavior in engineering.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section defines statically indeterminate structures and describes their analysis methods, including the flexibility method and stiffness method. It highlights the advantages of these structures, such as lower internal forces and redundancy, while noting their complexity in analysis. Requirements such as equilibrium and compatibility of displacements are emphasized, alongside examples demonstrating these principles.
Detailed
Detailed Summary
The analysis of statically indeterminate structures, which are characterized by having more unknowns than equations of equilibrium, involves specific methods that ensure the safety and functionality of the structure under various load conditions. Statically indeterminate structures offer advantages such as lower internal forces and redundancy. In case of failure of a support or member, these structures can redistribute internal forces, making them safer. However, the analysis of these structures is inherently more complex than that of statically determinate structures.
Key Points:
- Requirements: To effectively analyze statically indeterminate structures, it is essential to satisfy three primary requirements:
1. Equilibrium: The overall forces and moments in the system must balance.
2. Force-displacement relations: This is usually linear elastic, indicating how forces relate to displacements within the material.
3. Compatibility of displacements: This ensures there are no discontinuities in displacements across the structure.
- Analysis Methods: Two main methods are adopted in the analysis:
1. Flexibility Method: Useful when comparing internal forces relative to external imposed displacements.
2. Stiffness Method: Focuses on displacements resulting from known forces.
The methods are illustrated through examples such as a cable-supported rigid plate and a propped cantilever beam. Both cases emphasize the dependence of these structures on the elastic properties rather than just the external loads, showcasing the need to include material properties in the analysis.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Definition of Statically Indeterminate Structures
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
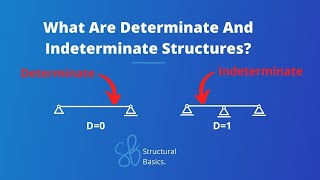
A statically indeterminate structure has more unknowns than equations of equilibrium (and equations of conditions if applicable).
Detailed Explanation
Statically indeterminate structures are those where the number of unknown forces exceeds the available equations to solve them. This often occurs in structures with multiple supports or members, making it impossible to determine the internal forces solely using static equilibrium conditions.
Examples & Analogies
Think of trying to solve a puzzle with missing pieces. If you have more questions to answer than clues available, you can't find a solution just with the clues. In the same way, a statically indeterminate structure has too many unknowns for the equations available.
Advantages of Statically Indeterminate Structures
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The advantages of statically indeterminate structures are: 1. Lower internal forces 2. Safety in redundancy, i.e., if a support or members fails, the structure can redistribute its internal forces to accommodate the changing boundary conditions without resulting in a sudden failure.
Detailed Explanation
Statically indeterminate structures can distribute loads more effectively due to the additional supports and member connections. This redundancy (the ability to withstand the failure of one component) enhances safety, allowing the structure to adjust to changes without collapsing suddenly. Additionally, because of the way forces are shared among multiple members, the internal forces in each member are lower than those would be in a statically determinate structure.
Examples & Analogies
Imagine a safety net for a circus performer. If one string of the net breaks, the remaining strings still hold the performer up, preventing a fall. Similarly, statically indeterminate structures can maintain stability even if one part fails.
Disadvantages of Statically Indeterminate Structures
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Only disadvantage is that it is more complicated to analyse.
Detailed Explanation
The complexity of analyzing statically indeterminate structures arises because the extra unknowns lead to a system of equations that is more intricate. This requires advanced methods, such as the flexibility method or stiffness method, to analyze the structure accurately. Unlike statically determinate structures, which can often be solved with basic static equilibrium equations, indeterminate structures require a deeper understanding of material properties and deformation.
Examples & Analogies
Consider baking a complex cake that needs multiple layers and decorations compared to a simple one-layer cake. The multi-layered cake requires more planning and care in execution, just as analyzing a statically indeterminate structure demands more detailed calculations and considerations.
Requirements for Analysis
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Analysis methods of statically indeterminate structures must satisfy three requirements: 1. Equilibrium 2. Force-displacement (or stress-strain) relations (linear elastic in this course). 3. Compatibility of displacements (i.e., no discontinuity).
Detailed Explanation
To ensure a successful analysis of a statically indeterminate structure, three core requirements must be met. First, the structure must be in equilibrium, meaning all forces and moments are balanced. Second, the relationship between forces and displacements must adhere to linear elasticity, which allows for predictable deformation under load. Third, all displacements throughout the structure must be compatible, indicating that they must not have any abrupt changes or discontinuities as forces are applied.
Examples & Analogies
Think about a well-orchestrated dance performance. The dancers must all move in harmony (equilibrium), follow the choreography (force-displacement relations), and ensure smooth transitions from one move to another (compatibility of displacements) to create a flawless show. In engineering structures, this level of coordination is crucial as well.
Classes of Solutions
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
This can be achieved through two classes of solution: 1. Force or Flexibility method; 2. Displacement or Stiffness method.
Detailed Explanation
To solve the equations resulting from the requirements mentioned above, engineers typically use one of two methods. The 'Flexibility Method' analyzes the structure by applying forces and examining how those forces cause displacements, focusing on member flexibility. On the other hand, the 'Stiffness Method' operates by looking at displacements first and determining the necessary forces, focusing on how rigid the structure is. Both methods have their advantages and specific applications depending on the situation.
Examples & Analogies
Imagine two different approaches to solving a maze. One player chooses to press through walls (flexibility method), testing each section to find a path, while the other carefully maps out each section before making their moves (stiffness method). Both methods can lead to the exit, but their approaches differ based on strategy and planning.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Statically Indeterminate Structures: Have more unknowns than equations of equilibrium, making analysis complex.
-
Flexibility Method: Focuses on the internal forces based on displacements.
-
Stiffness Method: Focuses on displacements that result from known forces.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
A cable-supported rigid plate with three unknown forces and two equilibrium equations.
-
A propped cantilever beam where the displacements depend on both the external loads and elastic properties.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
For a statically indeterminate view, more unknowns, that much is true!
📖 Fascinating Stories
-
Imagine a bridge with cables. If one cable snaps, others adjust to hold up the weight, showing redundancy.
🧠 Other Memory Gems
-
Remember the acronym 'EFC': Equilibrium, Force-Displacement Relations, Compatibility!
🎯 Super Acronyms
RUB. Redundancy, Uniqueness, Balance - key features of structures.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Statically Indeterminate Structure
Definition:
A structure with more unknown forces than the available equations of equilibrium.
-
Term: Equilibrium
Definition:
A state where all forces and moments acting on a structure are balanced.
-
Term: Compatibility
Definition:
The requirement that displacements in a structure must be continuous and without gaps.
-
Term: Flexibility Method
Definition:
An analysis method that relates internal forces to applied displacements.
-
Term: Stiffness Method
Definition:
An analysis method that relates displacements to applied forces.