Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Definition and Basics of Statically Indeterminate Structures
Unlock Audio Lesson
Let's define what a statically indeterminate structure is. It has more unknowns than equations of equilibrium, which adds complexity to its analysis.
So, why is that important? What's the main implication of having more unknowns?
Great question! This means we need to find extra equations or methods to solve for the unknowns. Statically indeterminate structures can handle loads better due to their redundancy.
So, does that mean they are always better than statically determinate ones?
Not always. While they provide safety in redundancy, their analysis is indeed more complex. Let's remember the phrase: 'With great flexibility, comes great complexity!'
Advantages of Statically Indeterminate Structures
Unlock Audio Lesson
Now, let's discuss the advantages. First, they often result in lower internal forces. What do you think that means?
Does it mean they can support more weight without breaking?
Exactly! Lower internal forces enhance performance. Next, there’s safety in redundancy. If one part fails, the structure can still carry loads effectively.
But what if yet another part fails?
Good thinking! That situation could indeed lead to failure, but the structure can handle a single failure without collapsing.
Analysis Requirements for Statically Indeterminate Structures
Unlock Audio Lesson
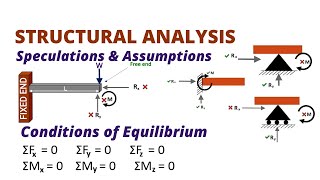
Let’s shift our focus to the analysis methods. There are three essential requirements: equilibrium, force-displacement relations, and compatibility of displacements.
What do you mean by equilibrium?
Equilibrium means all forces and moments acting on the structure must balance. Think of it like a see-saw; if one side is too heavy, it tips!
What about force-displacement relations?
That refers to understanding how forces relate to the resulting displacements based on material properties. This leads us to the next methods we can use for analysis.
Flexibility Method and Its Applications
Unlock Audio Lesson
The flexibility method is one common approach to analyze statically indeterminate structures. It allows us to calculate the internal forces based on known displacements.
Can you give an example of where we might see this applied?
Absolutely! Imagine a cable structure supporting a rigid plate; we would use the flexibility method to find forces in the cables based on how the plate displaces under loads.
That's interesting! But I bet it's way more complicated than in simpler structures.
Yes, it is! But that complexity allows for greater structural efficiency and safety.
Summary of Key Concepts
Unlock Audio Lesson
To summarize what we've learned, statically indeterminate structures offer lower internal forces and safety through redundancy but require more complex analysis methods.
The three analysis requirements are equilibrium, force-displacement relations, and compatibility, right?
Exactly! And the flexibility method is one of the key methods we use to analyze these structures.
I feel like I understood a lot more about why these structures are important now!
Great to hear! Understanding these concepts is crucial in structural engineering.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The 'Introduction' segment defines statically indeterminate structures and explains their analysis methods. It highlights advantages such as lower internal forces and redundancy for safety, as well as the associated complexity in analysis. It outlines the necessary conditions for analysis and introduces the flexibility method as a solution to such structures.
Detailed
Introduction to Statically Indeterminate Structures
A statically indeterminate structure is defined as having more unknowns than equations of equilibrium, meaning additional dependencies on external factors such as material properties. This characteristic provides several advantages:
1. Lower Internal Forces: These structures can have reduced internal stress, enhancing overall performance.
2. Safety in Redundancy: In case of member failure, they can redistribute loads, preventing sudden collapses.
However, the complexity of analysis rises, requiring methods that ensure:
1. Equilibrium: All forces and moments must be balanced.
2. Force-Displacement Relations: These structures are considered in a linear elastic context.
3. Compatibility of Displacements: No discontinuities should exist in the structural displacements.
The analysis can be approached via:
- Force (Flexibility) Method
- Displacement (Stiffness) Method
We exemplify these concepts using scenarios such as a cable-supported structure and a propped cantilever beam, further accentuating the reliance on elastic properties for determining forces.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Definition of Statically Indeterminate Structures
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
A statically indeterminate structure has more unknowns than equations of equilibrium (and equations of conditions if applicable).
Detailed Explanation
Statically indeterminate structures are those where there are more unknown forces than equations available to solve for them. In other words, you cannot figure out the forces just by using the basic rules of equilibrium (which state that the sum of forces and moments must equal zero). This situation typically arises in situations where the structure has more supports or members than strictly necessary.
Examples & Analogies
Think of trying to find the weight of several bags on a scale that can only show you the combined weight of two bags at a time. If you have more bags (unknowns) than the scale (equations) can compare, you won't be able to figure out the exact weight of each bag without more information.
Advantages of Statically Indeterminate Structures
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The advantages of statically indeterminate structures are:
1. Lower internal forces
2. Safety in redundancy, i.e., if a support or members fails, the structure can redistribute its internal forces to accommodate the changing B.C. without resulting in a sudden failure.
Detailed Explanation
Statically indeterminate structures are beneficial because they tend to have lower internal forces, which means they can safely withstand loads without excessive stress. Additionally, these structures can handle the failure of a support or member more gracefully. Instead of collapsing suddenly, they can redistribute the forces throughout the remaining structure, providing a safety advantage.
Examples & Analogies
Consider a team of workers on a project. If one person is unable to perform their task (like a support failing), the rest of the team can adjust and take on some of that person's work without the project falling apart. The redundancy means that there is backup available, much like the multiple paths for forces through a statically indeterminate structure.
Disadvantage of Statically Indeterminate Structures
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Only disadvantage is that it is more complicated to analyse.
Detailed Explanation
While statically indeterminate structures have many advantages, their analysis is more complex than that of statically determinate structures. This complexity arises because you need to consider the relationships between forces and displacements in more detail, often requiring advanced methods of analysis to find the internal forces and reactions.
Examples & Analogies
Imagine trying to solve a multi-layer puzzle instead of a simple one-layer puzzle. The multi-layer version requires you to understand how the different layers interact with each other, making it more intricate and time-consuming to complete.
Requirements for Analysis Methods
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Analysis methods of statically indeterminate structures must satisfy three requirements:
1. Equilibrium
2. Force-displacement (or stress-strain) relations (linear elastic in this course).
3. Compatibility of displacements (i.e., no discontinuity).
Detailed Explanation
To properly analyze statically indeterminate structures, you need to address three main criteria: First, the structure must be in equilibrium, meaning all forces and moments must balance. Second, you must account for the material properties and how they relate force to displacement, which often involves linear elastic behavior. Lastly, the displacements within the structure must be compatible, ensuring that there are no sudden changes that disrupt its continuity.
Examples & Analogies
Think of a bridge. For it to be safe and functional, all the sections must be stable (equilibrium), the materials must bend or compress predictably under load (force-displacement relations), and all parts must fit together without gaps or overlaps (compatibility of displacements).
Achieving Solutions in Statically Indeterminate Structures
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
This can be achieved through two classes of solution: Force or Flexibility method; Displacement or Stiffness method.
Detailed Explanation
When dealing with statically indeterminate structures, engineers use two primary methods to find solutions: the Flexibility Method, which focuses on how forces distribute and the reactions develop due to those forces, and the Stiffness Method, which emphasizes the displacements in the structure and how they relate to internal forces. Both methods have their own applications depending on the problem at hand.
Examples & Analogies
Consider two approaches to climbing a mountain. The first approach (Flexibility Method) involves figuring out the best route based on where you can put your weight safely, while the second approach (Stiffness Method) is based on how steep the climb is and planning your climbing techniques accordingly. Both methods help you reach the summit, but they do so through different strategies.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Statically Indeterminate Structure: More unknowns than equations leads to complex analysis.
-
Equilibrium: Forces must balance for a structure to be stable.
-
Flexibility Method: A method to analyze structures by calculating internal forces based on displacements.
-
Redundancy: The safety provided by the ability to redistribute loads during failure.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Example of a cable structure supporting a rigid plate, which uses a flexibility method for analysis.
-
Propped cantilever beam, demonstrating the complexities of statically indeterminate analysis.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
For structures, indeterminate, more unknowns, be sure to take care, find the balance, in the air!
📖 Fascinating Stories
-
Imagine a bridge where some beams can give way; others will hold, saving the day!
🧠 Other Memory Gems
-
R.E.F. - Remember Equilibrium, Force-displacement, Compatibility to analyze statically indeterminate structures.
🎯 Super Acronyms
S.I.S. - Statically Indeterminate Structures
- Safety in redundancy
- Internal force distribution
- Structural complexity.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Statically Indeterminate Structure
Definition:
A structure with more unknowns than equations of equilibrium.
-
Term: Equilibrium
Definition:
A state where all forces and moments acting on a structure are balanced.
-
Term: ForceDisplacement Relation
Definition:
A relationship that describes how applied forces result in deformations.
-
Term: Redundancy
Definition:
The ability of a structure to redistribute internal forces if a member fails.
-
Term: Flexibility Method
Definition:
An analysis approach that uses displacements to determine internal forces in structures.