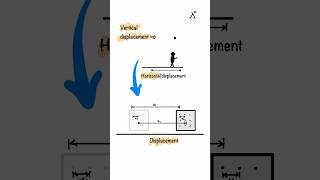
Compatibility of displacements
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Statically Indeterminate Structures
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Welcome, everyone! Today we're diving into statically indeterminate structures. Can anyone tell me what makes a structure statically indeterminate?

Is it because there are more unknowns than equations to solve them?

Exactly! These structures have more unknown internal forces than available equilibrium equations. This leads to complexity in analysis.

What does that mean for engineers working with these structures?

Great question! It means engineers need to apply methods like flexibility or stiffness to determine forces within the structure.

So, these structures can handle unexpected loads better because of redundancy?

Exactly! That's a key advantage. Redundancy allows redistribution of forces if one support fails.

In summary, statically indeterminate structures present unique challenges but also opportunities for safer engineering designs.
Compatibility of Displacements
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Let's talk about compatibility of displacements. Why is it essential in structural analysis?

It ensures there are no sudden changes in displacement, right?

Exactly! Compatibility ensures continuous displacement across the structure, which helps in maintaining integrity.

What happens if there is a discontinuity?

Good question! Discontinuities can lead to stress concentrations, ultimately risking structural failure.

I still find it confusing how to analyze these structures with the displacement methods.

No worries! We'll go step by step. We'll use examples of cable structures and cantilever beams next.

To recap: Compatibility of displacements ensures smooth performance in statically indeterminate structures, which is vital in our analysis.
Methods for Structural Analysis
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now, let’s focus on specific methods to analyze these structures. Can anyone name the two primary methods?

The flexibility method and the stiffness method.

Correct! The flexibility method relies on analyzing displacement, while the stiffness method focuses on forces.

Can we apply both methods to the same problem?

Indeed, that’s often done! Each method shines light on different aspects of the structure's behavior.

Okay, so in the flexibility method, we need to consider connections and how they deform under load?

Absolutely! Analyzing how each component deforms is crucial to ensuring compatibility.

In summary, understanding both methods lets us solve complex structural problems effectively.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
In analyzing statically indeterminate structures, compatibility of displacements ensures there are no discontinuities in displacements throughout the structure. This principle, alongside equilibrium conditions and force-displacement relationships, is fundamental in employing methods like flexibility and stiffness for structural analysis.
Detailed
Compatibility of Displacements
In the study of statically indeterminate structures, the compatibility of displacements is a crucial requirement. This concept ensures that all displacements across a structure are consistent and continuous, preventing any abrupt changes that could weaken the integrity of the structure.
Key Points:
- Definition of Statically Indeterminate Structures: These structures possess more unknowns than available equations of equilibrium, presenting unique complexities in their analysis.
- Importance of Compatibility: Compatibility guarantees that displacements are continuous, allowing engineers to apply either the Flexibility Method or the Stiffness Method for analysis. Each method serves to bridge the gap between internal forces and external loads, addressing how structural components respond to applied loads.
- Consequences of Incompatibility: Failure to ensure compatibility can lead to structural failures, as discontinuities in displacement lead to unforeseen stress concentrations.
- Example Problems: Throughout the section, illustrative problems demonstrate the process of analyzing forces in structures that adhere to the principles of compatibility, such as cable structures and cantilever beams.
Ultimately, mastering the concept of compatibility not only enhances analytical skills but also solidifies foundational knowledge in structural engineering principles.
Youtube Videos









Audio Book
Dive deep into the subject with an immersive audiobook experience.
Methods to Ensure Displacement Compatibility
Chapter 1 of 1
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
To achieve compatibility of displacements, engineers employ various methods such as the flexibility method and the stiffness method. The flexibility method focuses on expressing displacements in terms of forces and includes finding the flexibility matrix, which describes how displacements react to applied loads. Conversely, the stiffness method relates displacements directly to the stiffness characteristics of elements.
Detailed Explanation
Using the flexibility method, engineers can relate the resultant displacements to the applied forces on each structural component by using a flexibility matrix. This matrix helps in understanding how much the structure will deform under certain loads. On the other hand, the stiffness method uses stiffness coefficients, which are derived from material properties and geometry, to determine how forces affect the displacements. Both methods ensure that the displacements remain compatible throughout.
Examples & Analogies
Consider a rubber band and a metal rod being stretched. The rubber band (flexibility method) displays a large amount of stretch for a small increase in force, whereas the metal rod (stiffness method) will stretch much less for the same amount of force. By understanding the properties of both objects, you can predict how each will respond to being pulled, just like how engineers predict how different parts of a structure will deform under loads.
Key Concepts
-
Statically Indeterminate Structure: More unknowns than equations.
-
Compatibility of Displacements: Ensuring smooth displacement across structures.
-
Flexibility Method: Analyzes displacements to determine internal forces.
-
Stiffness Method: Analyzes forces to determine structural behavior.
-
Redundancy: Structural capability to handle failure through force redistribution.
Examples & Applications
Example of a cable system with two aluminum cables and one steel cable to analyze force distribution.
Propped cantilever beam demonstrating internal force evaluation through displacement analysis.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
In structures where forces are more, compatibility is what we adore.
Stories
Imagine a bridge built from many beams that must work together seamlessly. If one beam shifts suddenly, the whole bridge could crack, leading to collapse.
Memory Tools
Fifty Smooth Red Foxes to remember the Flexibility Method, Stiffness Method, Compatibility, Redundancy, and Structural stability.
Acronyms
SCAR for Statics, Compatibility, Analysis, Redundancy.
Flash Cards
Glossary
- Statically Indeterminate Structure
A structure with more unknown internal forces than available equations of equilibrium.
- Compatibility of Displacements
A principle ensuring continuous displacements across a structure without discontinuities.
- Flexibility Method
An analytical method that determines internal forces based on displacement.
- Stiffness Method
An analytical method focusing on determining structural forces directly.
- Redundancy
The ability of a structure to redistribute forces if a component fails.
Reference links
Supplementary resources to enhance your learning experience.
