Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Statically Indeterminate Structures
Unlock Audio Lesson
Today, we will explore statically indeterminate structures. Do any of you know how they differ from statically determinate structures?
I think they have more unknowns than equations of equilibrium.
Exactly! This means we can't solve them using simple equilibrium equations alone. They often rely on additional methods, like the flexibility method. Let's remember that with the acronym **FOC**: **F**lexibility, **O**verload, and **C**omplexity.
Can you explain more about the flexibility method?
Certainly! The flexibility method focuses on analyzing the structure's flexibility—or how it deforms—under loading conditions. It's an essential approach for understanding how to safely support different loads.
Example Analysis: Steel Building Frame
Unlock Audio Lesson
Let's discuss the steel building frame. There are three designs based on soil conditions. Who can summarize the first design?
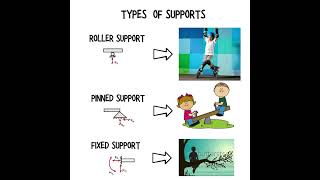
The first design utilizes a hinge and roller to account for poor soil conditions, minimizing horizontal force dependence.
Great! This approach enhances flexibility but requires careful analysis of forces. Why do you think understanding these designs is important?
It ensures the building can redistribute forces if one support fails, which adds safety.
Correct! That's one of the main advantages of using statically indeterminate structures.
Temperature Effects on Structures
Unlock Audio Lesson
Now, let's analyze how temperature affects our structures, especially with axial strain.
How does temperature cause change in structures?
Excellent question! A temperature change can cause materials to expand or contract, leading to changes in length. For example, a span can shorten, thus affecting overall structural alignment. This is crucial during hot and cold weather conditions.
So, it means we need to factor this into our designs, right?
Absolutely! Always remember to consider thermal effects in design with the **TIP** acronym: **T**emperature, **I**nternal forces, and **P**erformance.
Braced Bent Analysis
Unlock Audio Lesson
Finally, we'll examine braced bents. Can anyone describe what happens under lateral loads?
They can shift and may require added support to maintain stability.
Exactly! Our analysis table helps us organize forces into clear columns, especially with variable loads and temperature changes. Remember the order: **Actual load, Unit load, and Virtual force**.
Why do we analyze them separately?
Analyzing them separately allows us to isolate effects, making calculations simpler and more accurate. Pay attention to this organization!
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The examples focus on determining forces in structures using different support conditions and consider the effects of loading and temperature changes. It illustrates practical applications of the flexibility method and highlights the complexity involved in structural analysis.
Detailed
Detailed Summary
In this section, several examples provide insight into the analysis of statically indeterminate structures, particularly focusing on the flexibility method. The examples demonstrate how engineers address varying support conditions and the influence of external loads on structural behavior.
- Steel Building Frame Analysis: This example discusses three design approaches for a steel frame regarding differing soil conditions. Each design's structural analysis illustrates how redundancies ensure safety and adaptability in load-bearing scenarios.
- Effects of Temperature Changes: A critical component in structural analysis, particularly for materials sensitive to temperature variations, is examined through axial strain and curvature effects. The study quantifies changes in member lengths and the resulting impacts on structure performance.
- Braced Bent Example: The significance of redundants in trusses is highlighted as the analysis also considers temperature effects, lateral loads, and the evaluation of forces across the truss members. An organized tabular form summarizes necessary computations and reinforces understanding of the approach to analyzing displaced structures.
By employing these practical examples, students can visualize the complexities involved in structural engineering, reinforcing theoretical principles with real-world applications.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Steel Building Frame Analysis
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Example 10-1: Steel Building Frame Analysis, (White et al. 1976)
A small, mass-produced industrial building, Fig. 10.3, is to be framed in structural steel with a typical cross section as shown below. The engineer is considering three different designs for the frame: (a) for poor or unknown soil conditions, the foundations for the frame may not be able to develop any dependable horizontal forces at its bases. In this case the idealized base conditions are a hinge at one of the bases and a roller at the other; (b) for excellent...
Detailed Explanation
In this example, a structural engineer is tasked with designing a steel frame for a small industrial building. The design must account for varying soil conditions that could impact the stability and performance of the building. Three design scenarios are proposed: one where the soil conditions are poor, necessitating special support (a hinge and a roller), and two others for better soil conditions which allow for different types of support. Each choice affects the structural analysis and load distribution, thereby impacting safety and functionality.
Examples & Analogies
Imagine building a treehouse. If you're attaching it to a sturdy tree, you can use simple nails (like ideal conditions), but if the tree is weak or leaning, you might need ropes and hooks (like hinge and roller supports) to ensure it stays up safely.
Displacement due to Axial Strain
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
- In the following discussion, the contributions to displacements due to axial strain are denoted with a single prime (') and those due to curvature by a double prime ('').
-
Consider the axial strain first. A unit length of frame member shortens as a result of the temperature decrease from 85°F to 45°F at the middepth of the member. The strain is therefore
(\delta T = (0.0000055)(40) = 0.00022 - The effect of axial strain on the relative displacements needs little analysis. The horizontal member shortens by an amount (0.00022)(20) = 0.0044 ft. The shortening of the vertical members results in no relative displacement in the vertical direction 2. No rotation occurs.
Detailed Explanation
This part of the example focuses on how changes in temperature affect the frame's dimensions. When the temperature drops, the materials contract, causing a length change known as axial strain. In this case, the linear shortening of a horizontal beam is calculated based on the temperature drop. The explanation clarifies that while the horizontal member shrinks, the vertical members do not change in height, meaning there's no vertical displacement or rotation, simplifying the analysis.
Examples & Analogies
Think of a balloon filled with air. When it gets cold, the air inside cools down and takes up less space, causing the balloon to shrink a bit. If you have a long balloon shaped like a dog, it might not change in height, but its length decreases. So, while the dog balloon gets shorter, it stays upright without falling over.
Effect of Curvature and Virtual Work Method
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
- The effect of curvature must also be considered. A frame element of length dx undergoes an angular strain as a result of the temperature gradient. The change in length at an extreme fiber is
\(\epsilon = \delta T dx = 0.0000055(25)dx = 0.000138dx \) - with the resulting real rotation of the cross section
\(d\theta = \epsilon/0.5 = 0.000138dx/0.5 = 0.000276dx \) radians.
Detailed Explanation
Here, the focus shifts to how curvature (bending) in the frame affects its overall displacement. As the temperature changes, not only does the frame shorten (as previously discussed), but it also bends slightly due to thermal expansion, affecting angles between members. The calculations show how temperature changes lead to angular strains along the length of the material, which is critical for understanding the entire structural behavior under variable conditions.
Examples & Analogies
Picture a metal ruler left in the sun, which can heat up. As it warms, if it gets long enough in the heat, it may start to bow in the middle. Just as the bending of the ruler affects the angles it forms with other objects around it, the curvature in frame elements needs to be accounted for in structural analysis to ensure safety and usability.
Virtual Work Equation and Results
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
- A virtual force Q is applied in the direction of the desired displacement and the resulting moment diagram M determined. 11. The virtual work equation \(Q D = \int M d\theta \) is used to obtain each of the desired displacements D.
Detailed Explanation
This section explains the virtual work method, a powerful approach in structural analysis. When analyzing the structure, a hypothetical (or virtual) force is applied to determine how the displacement changes in response to external loads. By calculating the moments created by this force, engineers can use the virtual work equation to find actual displacements in the structure. This method allows for a systematic way to assess how structures respond under different loading conditions.
Examples & Analogies
Imagine you have a stretchy rubber band. If you pull on one end, the other end moves as well. If you take a friend to help pull on the rubber band, you can visualize how far it stretches by measuring the length at various points. Here, applying a virtual force is like having multiple people pulling on different parts of the rubber band—that helps you understand how each part responds to the overall force.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Statically Indeterminate Structure: A structure with more unknowns than equations.
-
Flexibility Method: An analytical technique to evaluate the response of a structure to loads.
-
Temperature Influence: The effects of thermal expansion or contraction impacting structural calculations.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Example of a steel building frame: involving different support conditions.
-
Effect of temperature changes: analyzing axial strain and its impact on structure length.
-
Braced bent analysis under lateral loads.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
When structures fear to collapse and bend, remember the flexibility method is your friend.
📖 Fascinating Stories
-
Imagine a tall building that shakes in the wind, every beam must adjust to avoid a sad end.
🧠 Other Memory Gems
-
Use 'TIP' for Thermal effects: Temperature, Internal forces, Performance.
🎯 Super Acronyms
Remember FOC**
- F**lexibility
- **O**verload
- and **C**omplexity for structures.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Statically Indeterminate
Definition:
Structures that have more unknown forces or displacements than equations of equilibrium available.
-
Term: Flexibility Method
Definition:
A structural analysis technique focusing on the flexibility or deformation of a structure under load.
-
Term: Axial Strain
Definition:
The deformation of material due to tension or compression along a particular axis.
-
Term: Thermal Effects
Definition:
Changes in physical dimensions of materials due to temperature variations, affecting structural integrity.