Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skillsβperfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Overview of Placement Algorithms
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Today, we're discussing the role of placement algorithms in VLSI design. Can anyone tell me why placement is crucial?
Isn't it to arrange the components correctly on the chip?
Exactly! Placement is essential for minimizing wirelength, meeting timing constraints, and ensuring controlled density. Remember, efficient placement can significantly impact the circuit performance.
What are the key goals of these placement algorithms?
Great question! The main goals include wirelength minimization, timing optimization, and density control, which ensures that the design does not create congestion. An acronym to remember is WTD: Wirelength, Timing, Density.
Can you explain what density control means?
Sure! Density control involves ensuring that cells are placed in a way that avoids overcrowding, which can lead to manufacturing issues. Let's keep WTD in mind as we explore specific algorithms.
Simulated Annealing in Placement
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Letβs talk about Simulated Annealing, or SA. Who can describe how it operates in placement?
Isnβt it a method that improves placements by iteratively adjusting positions?
Correct! It starts with a random placement and improves upon it by minimizing a cost function related to wirelength. The temperature in SA helps it escape local minima. Think of it like cooling metal to achieve the best shape.
Can it guarantee the best solution?
Not necessarily; it finds near-optimal solutions but isn't always perfect. This is a trade-off between speed and accuracy. Remember, SA is excellent for exploring multiple solutions!
Greedy Algorithms and Their Limitations
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Next, letβs delve into Greedy Algorithms. Who can summarize their approach?
They place cells one at a time based on the best immediate position.
Exactly! They make quick decisions based on current evaluations of placement cost. But whatβs a drawback of using Greedy Algorithms?
They might miss the best overall arrangement since they only consider immediate benefits.
Well put! So, while Greedy algorithms are faster, they can sometimes lead to suboptimal solutions. They are best when rapid placement is needed.
Quadratic Programming and Partitioning
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now, letβs explore Quadratic Programming. What do we know about it in terms of placement?
Itβs an optimization method that deals with minimizing quadratic functions under constraints, right?
Correct! This approach gives high-quality solutions that account for both wirelength and timing constraints. What about Partitioning-Based Placement?
It involves dividing the design into smaller partitions to manage complexity during placement.
Exactly! Iterative refinement within partitions reduces congestion. Think of it as organizing your workspace into manageable sections!
Recap and Importance of Placement Algorithms
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
To wrap up, can anyone summarize the key algorithms we discussed in placement?
We talked about Simulated Annealing, Greedy Algorithms, Quadratic Programming, and Partitioning!
Great! And remember, each has its strengths and weaknesses, making them suitable for different design challenges. Efficient placement can lead to better performance in the final VLSI product. Always consider the specific needs of your design!
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
Placement algorithms are crucial in VLSI design for optimally positioning cells to minimize wirelength, ensure timing constraints, and manage density. This section outlines various algorithms including Simulated Annealing, Greedy Algorithms, Quadratic Programming, and Partitioning-Based Placement, discussing their functionalities and applications.
Detailed
Placement Algorithms in VLSI Design
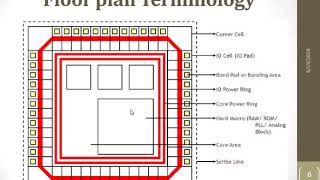
Placement algorithms are integral to the VLSI physical design process, focusing on the optimal arrangement of standard cells or blocks after establishing a floorplan. The primary goals include minimizing total wirelength, ensuring that timing constraints are met, and maintaining proper density to avoid manufacturing issues.
These algorithms can be categorized into global placement and detailed placement. Global placement involves the initial cell distribution to roughly minimize wirelength, while detailed placement refines this arrangement considering specific constraints, like cell overlap.
Key algorithms discussed include:
- Simulated Annealing: A heuristic inspired by metallurgy that iteratively improves placements by minimizing cost functions, leveraging a temperature parameter to escape local minima.
- Greedy Algorithms: Quick placement methods that select optimal positions based on immediate cost metrics, though they may miss global optima.
- Quadratic Programming: This optimization-based approach seeks to minimize quadratic functions under defined constraints, offering high-quality solutions.
- Partitioning-Based Placement: Involves dividing layouts into smaller segments and refining placements within these partitions to enhance efficiency and reduce congestion.
By employing these algorithms, designers can achieve effective layouts that improve performance, reduce power consumption, and enhance manufacturability in the resultant integrated circuits.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Simulated Annealing (SA)
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
β Simulated Annealing (SA): Similar to its use in floorplanning, simulated annealing is also widely used in placement algorithms. It starts with a random placement and iteratively improves the placement by minimizing a cost function (e.g., wirelength, timing, or congestion). The temperature parameter in simulated annealing allows the algorithm to escape local minima, leading to better solutions.
Detailed Explanation
Simulated Annealing is a probabilistic technique used to find approximate solutions to optimization problems. It operates by starting with a random arrangement of the elements (in this case, standard cells on a chip), then it makes iterative adjustments to their positions. Each adjustment is aimed at reducing a defined cost, which might involve factors like the total length of wiring required (wirelength), the timing required for signals to travel (timing), or how congested the layout becomes (congestion).
The unique aspect of Simulated Annealing is its use of a 'temperature' parameter. This temperature gradually decreases, allowing the algorithm to avoid getting stuck in a local minimumβa solution that is good but not the best. When the temperature is high, there is a higher chance of accepting changes that worsen the current solution, which helps the algorithm explore more of the solution space. As the temperature decreases, the algorithm becomes more conservative, focusing on fine-tuning the placement for the best results.
Examples & Analogies
Imagine adjusting the arrangement of furniture in a room to make it more spacious and functional. You start with a random layout (similar to a random cell placement), and then you try different arrangements (the iterations). At first, you might change things around radically, even if it seems to make the room feel more cramped (like accepting worse solutions to escape local minima). However, over time, you notice which configurations work better, and you start making smaller adjustments to enhance comfort and space efficiency, much like the algorithm stabilizes at lower temperatures to refine its solution.
Greedy Algorithms
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
β Greedy Algorithms: Greedy placement algorithms iteratively place cells by selecting the best position for each cell based on a given cost metric, such as the shortest wirelength to other cells. Although faster than simulated annealing, greedy algorithms are often not as effective at finding the global optimum.
Detailed Explanation
Greedy algorithms operate on the principle of making the most immediate best choice at each step. In the context of placement algorithms, this means that each cell is placed one by one, choosing the position that offers the best cost metric at that moment, commonly focusing on minimizing wirelength to surrounding cells. While this approach is straightforward and quick, making decisions based only on current local information doesn't guarantee the best overall result for the entire layout. This can sometimes lead to suboptimal placements where better global arrangements are overlooked because the algorithm didnβt consider future placements.
Examples & Analogies
Think of a chef preparing multiple dishes. If the chef focuses entirely on optimizing the cooking time for each dish separately, they might miss the bigger picture of how different timings affect the meal's presentation and serving. For instance, if a side dish takes longer to cook and the main dish has to wait, the entire meal's dining experience might suffer. Similarly, greedy placement can lead to quick solutions but might not yield the best configuration when viewed as a whole.
Quadratic Programming
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
β Quadratic Programming: This method is used to solve placement problems in which the objective is to minimize a quadratic function (e.g., wirelength) subject to certain constraints (e.g., timing). Itβs an optimization-based approach that provides high-quality solutions.
Detailed Explanation
Quadratic Programming (QP) is a mathematical strategy used to find the best outcome from a set of variables while following a specific structureβusually something that involves a quadratic cost function. In placement algorithms, QP seeks to minimize specific criteria like wirelength while adhering to constraints such as timing requirements. This optimization method involves setting up equations that define these relationships, allowing the algorithm to calculate the most effective placement of the structural elements on the chip to achieve minimal wirelength while obeying necessary timing rules.
Examples & Analogies
Consider planning a public transport route in a city. You want to minimize the distance the transport vehicles travel (the wirelength) but must also ensure that they arrive at major stops within a certain time frame (the constraints). Using quadratic programming is like employing a strategic math model that weighs these factors against each other to find the most efficient route for all vehicles while satisfying timeliness constraints.
Partitioning-Based Placement
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
β Partitioning-Based Placement: These algorithms divide the layout into manageable partitions and perform placement within each partition. The partitions are then refined iteratively, and this approach helps to reduce congestion and wirelength.
Detailed Explanation
Partitioning-Based Placement breaks down the complex layout of the chip into smaller, manageable sections or partitions. Each partition is analyzed independently, allowing for more straightforward optimization processes within each small area. After initial placements are made, the algorithm refines the positions iteratively, which helps to reduce issues like congestion that can arise from tightly packed areas and aim for overall wirelength minimization. This method improves the efficiency of placement algorithms by simplifying the challenge of fitting all components onto the chip.
Examples & Analogies
Imagine organizing a large library; instead of trying to sort every book in one go, you first divide the shelves into sections (fiction, non-fiction, reference, etc.). By organizing one section at a time, it becomes easier to manage space and keep similar genres together. This method reduces the chaos of having a single massive pile of books spread out, just as partitioning in placement reduces congestion and optimizes placement efficiency step-by-step.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Placement Objectives: Placement aims to minimize wirelength, meet timing constraints, and control density.
-
Simulated Annealing: A heuristic method that allows for iterative improvement in placements by escaping local minima.
-
Greedy Algorithms: Quick algorithms that make immediate choices, often missing out on global optimal solutions.
-
Quadratic Programming: An optimization method effective in minimizing wirelength under constraints.
-
Partitioning-Based Placement: Involves dividing the circuit layout into smaller sections to improve placement efficiency.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
In a circuit with multiple interconnected components, a placement algorithm positions clusters of related components close together to minimize wirelength and reduce latency.
-
Simulated Annealing iteratively improves a random initial layout by adjusting positions based on a wirelength cost function in real-time.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
π΅ Rhymes Time
-
In placement we strive, to keep wirelength alive. With timing in view, our designs break through!
π Fascinating Stories
-
Imagine a busy city where streets are designed stubbornly. Placing buildings without planning creates jams. But when organized, the traffic flows smooth!
π§ Other Memory Gems
-
WTD: Remember Wirelength, Timing, Density when you think of placement goals!
π― Super Acronyms
S.G.Q.P
- Simulated
- Greedy
- Quadratic
- Partitioning - the algorithms for our placement expedition!
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Placement Algorithms
Definition:
Techniques used to determine the optimal positioning of cells in VLSI design.
-
Term: Simulated Annealing
Definition:
A heuristic optimization method that mimics the annealing process in metallurgy for improving placements.
-
Term: Greedy Algorithms
Definition:
Placement methods that select the best immediate option for positioning without considering future consequences.
-
Term: Quadratic Programming
Definition:
An optimization technique that computes placements by minimizing quadratic functions subject to constraints.
-
Term: PartitioningBased Placement
Definition:
An approach that divides the layout into smaller sections to optimize cell placements within them.