Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skillsβperfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Routing in VLSI
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Welcome everyone! Today we're discussing routing in VLSI design. Can anyone tell me what routing means in this context?
Isn't it about connecting different blocks or cells in the circuit?
Exactly! Routing is about ensuring all components are correctly connected while minimizing wire length to prevent delays. Why do you think minimizing wire length is important?
Because shorter wires can help reduce signal delay and power consumption?
Great point! Minimizing wire length is indeed vital for efficient design. Now, let's explore specific routing algorithms.
Maze Routing
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
One of the fundamental algorithms we use is Maze Routing. Can anyone explain how it works?
I think it finds the shortest path in a grid while avoiding obstacles?
That's right! It uses a breadth-first search methodology. Can you remember any scenarios where this would be particularly useful?
Maybe in complex designs where there are many obstacles between connections?
Exactly! Its ability to navigate around obstacles makes it ideal for intricate layouts.
Lee's Algorithm
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Next, let's talk about Lee's Algorithm. How does it differentiate from standard maze routing?
Doesn't it use a wave propagation technique to explore the grid?
Absolutely! This method is effective for smaller designs. Why do you think wave propagation is advantageous?
It probably allows the algorithm to efficiently find paths, right?
Exactly! It's efficient in early routing steps. Fantastic engagement, everyone!
A* Algorithm
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now, let's move on to the A* Algorithm. Who remembers its unique features?
It evaluates both the cost to the current point and the estimated cost to the destination, right?
Correct! This method allows efficient searching for both global and detailed routes. Can anyone think of an advantage of using A*?
It balances efficiency with the need for accuracy in routing?
Exactly! It finds efficient pathways without compromising too much on resources.
Global Routing with Steiner Trees
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Lastly, let's discuss Global Routing with Steiner Trees. What do you know about this method?
I remember it involves adding points to improve routing efficiency.
That's right! By introducing Steiner points, it helps minimize wirelength effectively. Can anyone give an example of when we'd use this?
In very dense circuits where wire length is critical?
Exactly! It's particularly useful in complex designs. Great job summarizing todayβs key points!
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
Routing is a crucial stage in VLSI design that connects various blocks of a circuit. This section highlights key routing algorithms, such as Maze Routing, Lee's Algorithm, A*, and Steiner Trees, each of which plays a vital role in ensuring effective and efficient connections within the chip design.
Detailed
Detailed Summary of Routing Algorithms
Routing is the essential process in VLSI design that connects the physical blocks placed within the integrated circuit. This section focuses on various routing algorithms that are integral to this process, aiming to achieve efficient connections that minimize total wirelength while avoiding congestion and maintaining the power requirements of the design.
- Maze Routing: This classical routing algorithm finds the shortest path between two points in a grid layout while avoiding obstacles. It employs a breadth-first search method, exploring all potential paths to identify an optimal route.
- Lee's Algorithm: A variation of maze routing, Lee's Algorithm uses a wave propagation technique to navigate through the layout efficiently. It's particularly advantageous in the early routing stages for smaller designs.
- A* Algorithm: The A* pathfinding algorithm evaluates the cost of reaching a particular point alongside the estimated cost to the destination. It balances performance and computational efficiency, making it suitable for both global and detailed routing steps.
- Global Routing with Steiner Trees: This method gets its efficiency from utilizing Steiner trees, which introduce additional points (Steiner points) to improve overall routing efficiency, particularly beneficial for minimizing wirelength compared to traditional methods.
These routing algorithms are crucial for transforming logical designs into physical implementations, ensuring that they adhere to performance specifications while optimizing area and power constraints.
Youtube Videos
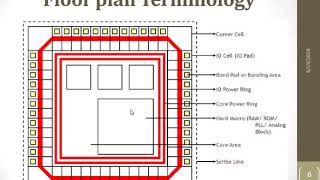
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Overview of Routing Algorithms
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Routing algorithms are crucial in VLSI design as they determine how the various blocks or cells are interconnected on the chip. The effectiveness of routing has a direct impact on performance, power consumption, and overall design efficiency.
Detailed Explanation
Routing algorithms work by calculating pathways for electrical signals to travel between different parts of a chip. Since these algorithms affect areas like length of wiring and timing of signal transmission, they play a vital role in achieving an efficient design. The algorithms ensure that there are minimal delays and that the layout meets the required specifications for power usage and timing.
Examples & Analogies
Think of routing algorithms like the way a city planner maps out roads for cars. Just as a well-planned road network reduces traffic and travel times, effective routing minimizes the distance signals must travel and prevents congestion within the circuitry.
Maze Routing
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Maze Routing is a classical routing algorithm used for finding the shortest path between two points while avoiding obstacles. It works by exploring all possible paths from the source to the destination in a grid-based layout, using a breadth-first search algorithm to find the optimal route.
Detailed Explanation
The Maze Routing algorithm functions like navigating a maze where the objective is to find the shortest way out. It examines all available routes from the start point to ensure it chooses the most direct path while avoiding any obstructions. This method is particularly useful when determining routing paths on chip layouts where potential obstacles exist.
Examples & Analogies
Imagine you are in a corn maze trying to find the exit. You would methodically check each path, remembering which ones are blocked until you find the shortest way out. Maze Routing does the same for electronic signals.
Leeβs Algorithm
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Leeβs Algorithm is a variation of maze routing, which uses a wave propagation technique to explore the grid and find the shortest path. It is widely used in early routing steps and is efficient for small designs.
Detailed Explanation
Lee's Algorithm enhances the basic maze routing by employing a wave-like method to propagate through the grid, enabling it to identify the shortest path more effectively. It starts by marking points reachable from the source and propagating until it finds the destination. This makes it particularly effective for smaller designs, allowing for rapid evaluation of potential paths.
Examples & Analogies
This method can be likened to throwing a stone into a pond and watching the ripples radiate outward until they reach a certain point. The ripples represent possible paths being explored until Lee's Algorithm finds the best route to the destination.
A* Algorithm
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The A* algorithm is a well-known pathfinding algorithm that finds the shortest path by evaluating both the cost to reach the current point and the estimated cost to reach the destination. Itβs used for both global and detailed routing in VLSI designs, balancing between performance and computational efficiency.
Detailed Explanation
A Algorithm combines the best features of both breadth-first search and heuristic-based searches. By considering not only the cost to travel to the current node but also factoring in a heuristic that estimates the distance to the target, A is able to find optimal paths efficiently, making it suitable for complex routing tasks in VLSI design.
Examples & Analogies
Imagine planning a road trip: you not only consider the distance to each stop but also the expected traffic conditions that might delay the journey. A* Algorithm does the same by weighing the distance to travel against potential obstacles or delays.
Global Routing with Steiner Trees
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
In this method, global routing aims to minimize the total wirelength by using Steiner trees, which are more efficient than using simple shortest-path algorithms like maze routing. Steiner trees involve adding extra 'helper' points (called Steiner points) to improve routing efficiency.
Detailed Explanation
Steiner Trees work by identifying optimal connections that reduce the total distance needed for wiring by introducing additional points. It analyzes combinations of points and connections to create a routing strategy that minimizes wire length and enhances performance, especially in complex layouts.
Examples & Analogies
Consider a scenario where you want to connect three cities with the shortest possible road network. Instead of drawing straight lines between each pair of cities, adding a fourth city as a connector can lead to a shorter overall distance. Steiner Trees exploit this concept by introducing helper points strategically.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Routing: The process of connecting different components in VLSI design to form a complete circuit.
-
Wirelength Minimization: The goal of reducing the total length of connecting wires to enhance performance and reduce power consumption.
-
Routing Algorithms: Specialized methods employed to achieve efficient routing in integrated circuit designs.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
In a complex circuit design, utilizing the A* algorithm may significantly reduce the time taken to find optimal paths between multiple components.
-
Applying Steiner Trees can help in a large VLSI circuit where minimizing wire length is essential to prevent timing issues.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
π΅ Rhymes Time
-
In the maze we find our way, shortest path is what we say.
π Fascinating Stories
-
Imagine you're a postman delivering letters. You have to find the shortest path on a city grid, dodging traffic jams β this is like Maze Routing.
π§ Other Memory Gems
-
Remember the M.L.A.S. for Route Success: Maze, Lee, A*, Steiner.
π― Super Acronyms
RATS
- Routing Algorithms for Total Success in minimizing wirelength.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Maze Routing
Definition:
A classical algorithm used to find the shortest path between two points on a grid while avoiding obstacles.
-
Term: Lee's Algorithm
Definition:
A variation of maze routing that uses wave propagation to find the shortest path in VLSI design.
-
Term: A* Algorithm
Definition:
A pathfinding algorithm that evaluates the cost of reaching a point and estimates the cost to target, balancing efficiency.
-
Term: Steiner Trees
Definition:
A method that introduces additional nodes (Steiner points) to improve routing efficiency and minimize total wirelength.