Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Gauss's Law for Magnetism
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Today, we're going to discuss Gauss's law for magnetism, which is fundamentally different from what we learned about electric fields. Does anyone remember the basic idea of Gauss's law?
Yes, it relates the electric field to the charge enclosed by a surface.
Exactly! Now, for magnetism, we have a unique situation. Gauss's law for magnetism tells us that the total magnetic flux through any closed surface is zero. Can someone explain why that is?
Because there are no magnetic monopoles?
Correct! Magnetic field lines form continuous loops, and the number of lines entering a closed surface must equal the number leaving it.
So, it's like all magnetic field lines are connected?
Exactly! You're doing great. Remember, a key point here is understanding that in contrast to electric fields, magnetic fields don’t originate from positive or negative charges.
The Mathematical Expression of Gauss's Law for Magnetism
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Let’s talk about the mathematical expression for Gauss's law for magnetism. Can anyone recall what the formula looks like?
Is it similar to the electric field flux equation?
Yes, but instead of electric charge, we find that the magnetic flux through a closed surface equals zero. It can be written as: ∮ B · dS = 0. What does this signify?
It confirms that the flux inside and outside the surface is always balanced.
Well said! Let’s visualize this with some diagrams. If we look at a Gaussian surface, can anyone tell me what that would represent?
It’s a hypothetical surface used to analyze the behavior of the magnetic field.
Yes! And when we consider it, we always find that the magnetic field lines don’t originate or terminate within that closed surface.
Differences from Gauss's Law for Electrostatics
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now, let's discuss how Gauss's law for magnetism differs from electrostatics. What would you say is the biggest difference?
In electrostatics, the flux is related to the charge inside, while in magnetism, it's always zero.
Absolutely! The implications of magnetic monopoles or the lack thereof shape our understanding of magnetism. Is anyone familiar with why this absence is important?
It shows how magnetism is fundamentally different, and we can't have isolated poles.
Exactly! This understanding has profound implications in both theoretical and applied physics.
Real-Life Applications of Gauss's Law for Magnetism
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Let's discuss some real-world applications of Gauss's law for magnetism. How do you think this principle might be useful?
It could help design magnetic shielding or equipment in electrical engineering.
Correct! In devices like transformers or MRI machines, understanding the flow of magnetic fields is crucial. What else?
It might be used when dealing with magnetic materials to understand their behavior.
Excellent point! Mastering these principles enables us to innovate and improve technologies.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
This section introduces Gauss's law for magnetism, contrasts it with Gauss's law for electrostatics, and highlights the significant differences, including the absence of isolated magnetic monopoles in nature and demonstrating that magnetic field lines form continuous closed loops.
Detailed
Detailed Summary of Gauss's Law for Magnetism
In this section, we explore Gauss's law for magnetism, which states that the net magnetic flux through any closed surface is zero. Unlike electrostatics, where the flux through a closed surface is directly related to the charge enclosed, magnetic fields do not have sources or sinks because isolated magnetic poles (monopoles) have not been observed. The continuous nature of magnetic field lines is emphasized through various closures of Gaussian surfaces. We analyze the mathematical formulation of this law, denoting magnetic flux through a small vector area element and establishing that the total magnetic flux over any closed surface sums to zero. This conceptual understanding is fundamental in understanding not only magnetism but also the behavior of magnetic fields in practical applications.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Gauss's Law for Magnetism
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
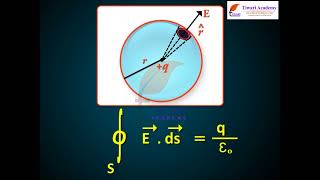
In Chapter 1, we studied Gauss’s law for electrostatics. In Fig 5.2(c), we see that for a closed surface represented by i, the number of lines leaving the surface is equal to the number of lines entering it. This is consistent with the fact that no net charge is enclosed by the surface. However, in the same figure, for the closed surface ii, there is a net outward flux, since it does include a net (positive) charge. The situation is radically different for magnetic fields which are continuous and form closed loops.
Detailed Explanation
The opening segment introduces the concept of Gauss’s law for magnetism by comparing it with electrostatics. In electrostatics, if you visualize a closed surface (like a balloon), the electric field lines either enter or exit the surface depending on the presence of an electric charge inside the surface. If there’s no charge, the number of lines entering equals the number leaving. However, for magnetic fields, they behave differently. Magnetic field lines are always continuous loops, meaning what goes in must come out. Since there are no isolated magnetic charges, the magnetic flux through any closed surface is always zero.
Examples & Analogies
Think of a crowded theater filled with people (magnetic field lines) moving in and out. If someone leaves the theater (field line exiting), another must enter (field line entering) at the same time to keep the number of people inside (net magnetic flux) constant. If no one enters or exits, the number inside remains the same (zero net flux through the magnetic surface).
Magnetic Flux Through a Closed Surface
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Consider a small vector area element ∆S of a closed surface S as in Fig. 5.5. The magnetic flux through ΔS is defined as Δφ = B.ΔS, where B is the field at ΔS. We divide S into many small area elements and calculate the individual flux through each. Then, the net flux φ is, φ = (∑ Δφ) = ∑ (B · ΔS) = 0.
Detailed Explanation
We consider a small piece of any closed surface, represented by ∆S. The magnetic flux (the measure of the quantity of magnetic field passing through that surface) can be determined for that small piece first by calculating the product of the magnetic field B and the area ΔS it covers. To find the total magnetic flux through the entire closed surface, we sum up all these small contributions. In accordance with Gauss's law for magnetism, when we sum them all together, we find the total magnetic flux through any closed surface is zero. This emphasizes the nature of magnetic fields being non-diverging, unlike electric fields that can have sources or sinks.
Examples & Analogies
Imagine measuring water flow through a series of connected pipes (the surface). If every drop of water entering a pipe (analogous to a magnetic field line entering a closed surface) is matched by a drop leaving, the total flow inside the space (net flux) is zero. You can visualize this with a sponge in water, constantly absorbing and releasing the same amount of water around it—what goes in must come out!
Magnetic Dipoles: The Basis of Gauss's Law
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The difference between the Gauss’s law of magnetism and that for electrostatics is a reflection of the fact that isolated magnetic poles (also called monopoles) are not known to exist. There are no sources or sinks of B; the simplest magnetic element is a dipole or a current loop. All magnetic phenomena can be explained in terms of an arrangement of dipoles and/or current loops. Thus, Gauss’s law for magnetism is: The net magnetic flux through any closed surface is zero.
Detailed Explanation
This section emphasizes the fundamental aspect that sets magnetism apart from electrostatics: the absence of isolated magnetic poles. Unlike electric charges, which can exist independently as positive or negative, all magnets have both a north and a south pole. When we speak of magnetic fields, we're dealing with magnetic dipoles (which have a north and south pole). Thus, they always pair up, ensuring that when we calculate the total magnetic flux through a closed surface, we get zero, as there are no starting or ending points for magnetic lines in isolation.
Examples & Analogies
Consider a bar magnet. If you were to cut it in half, you don't end up with a north pole and a south pole separately; instead, each half becomes a smaller magnet, still having both a north and south pole. It's a continuous cycle, much like breaking a chocolate bar where the individual pieces still retain a top and bottom.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Gauss's Law for Magnetism: The net magnetic flux through any closed surface is zero.
-
Magnetic Field Lines: Magnetic field lines form continuous loops, without beginning or end.
-
Gaussian Surface: A closed surface used in the application of the laws of physics.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
An example of using Gauss's law is in determining the magnetic field around a solenoid, where the magnetic fields outside the cylinder are negligible compared to the inside.
-
In laboratory setups, physicists create Gaussian surfaces to visualize and calculate the effects of surrounding magnetic fields.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
In magnetism's closed-loop play, flux is zero every day.
📖 Fascinating Stories
-
Imagine a magical forest; everywhere you go, the wind blows in circles. This is like magnetic fields - always connected, never alone, just like Gauss’s law says – flux is balanced.
🧠 Other Memory Gems
-
Remember: 'Zero flux' for Gauss means 'Absolutely No Monopoles'!
🎯 Super Acronyms
MELT - Magnetic Envelopes Look Troubling - That's why we visualize them with Gaussian surfaces!
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Gauss's Law for Magnetism
Definition:
States that the net magnetic flux through any closed surface is zero.
-
Term: Magnetic Flux
Definition:
The measure of the amount of magnetic field passing through a given area.
-
Term: Magnetic Monopoles
Definition:
Hypothetical particles that would be magnetic charges, not yet observed in nature.
-
Term: Gaussian Surface
Definition:
An imaginary closed surface used to apply Gauss's law.