Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skillsβperfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
The Significance of Block Diagrams
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Today, we're concluding our discussion on block diagrams. To start, can anyone tell me why block diagrams are important in control systems?
They help simplify complex systems!
Exactly! They allow us to break down complex systems into manageable parts. This helps in analyzing the time and frequency responses effectively. Can someone explain how they assist in time domain analysis?
They let us visualize how the system reacts over time to different inputs.
Right! By using block diagrams, we're able to track the output response as we apply different inputs, making it easier to manage and predict performance.
Frequency Domain Insights
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now, how do block diagrams help us understand frequency domain analysis?
They help determine the system's stability and response over different frequencies.
Exactly! By plotting the frequency response, we can visualize how oscillations affect system stability. What kind of plots can you use for this purpose?
Bode and Nyquist plots!
That's correct! Each plot provides crucial information about gain and phase, helping us assess system behavior.
System Design Implications
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Lastly, how do block diagrams facilitate system design?
They provide a clear structure for understanding system behavior and performance measures.
Absolutely! Engineers can identify critical components and potential weaknesses in the system design through this clear visualization. Why is it crucial to have a good design in control systems?
To ensure stability and optimal performance!
Exactly! A well-designed system minimizes errors and enhances performance.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
This section emphasizes the importance of block diagrams in simplifying the representation of control systems, aiding in both time and frequency domain analyses. It highlights how these diagrams help engineers understand and design systems effectively.
Detailed
Conclusion
Block diagrams are powerful tools for representing and analyzing control systems in both the time and frequency domains. In the time domain, they help visualize the system's response to various inputs, while in the frequency domain, they provide insights into system stability, bandwidth, and resonance. By reducing complex systems into manageable blocks, engineers can better understand and design systems with desired performance characteristics.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
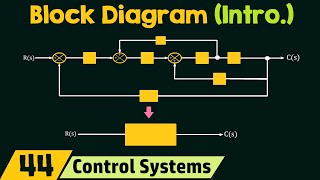
Power of Block Diagrams
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Block diagrams are powerful tools for representing and analyzing control systems in both the time and frequency domains.
Detailed Explanation
Block diagrams serve as a crucial visualization tool in control systems engineering. They simplify the representation of complex systems, making it easier to understand the relationships between different components and how they interact over time and frequency. By breaking down a system into blocks, engineers can focus on individual components without losing sight of the overall functionality.
Examples & Analogies
Think of block diagrams like a city map. Just as a city map shows various neighborhoods, roads, and connections, a block diagram illustrates the different parts of a control system and how they connect. This allows anyone looking at the map to visualize where each part is located and how they all interact, making navigation easier.
Time Domain Insights
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
In the time domain, they help visualize the system's response to various inputs.
Detailed Explanation
When analyzing systems in the time domain using block diagrams, engineers can assess how the system reacts to input signals over time. This helps in identifying the transient behavior of the system, including how quickly it reaches a steady state after a disturbance and how it responds to changing inputs. By visualizing these responses, engineers can make adjustments to improve performance.
Examples & Analogies
Consider a car's acceleration: when you press the gas pedal (the input), the car's speed increases (the output) over time. An engineer uses block diagrams to study how fast the car accelerates after pressing the pedal and how smooth the acceleration is. This analysis helps improve car performance to ensure a better driving experience.
Frequency Domain Insights
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
In the frequency domain, they provide insights into system stability, bandwidth, and resonance.
Detailed Explanation
Block diagrams can also represent how systems behave in the frequency domain. This allows engineers to analyze characteristics such as stability (how a system reacts to frequency inputs), bandwidth (the range of frequencies a system can effectively process), and resonance (the tendency of a system to oscillate at certain frequencies). Understanding these factors is crucial for designing systems that operate reliably across various conditions.
Examples & Analogies
Imagine tuning a musical instrument like a guitar. Each string vibrates at a specific frequency, and if you pluck one, it resonates with a particular sound. Engineers use block diagrams to ensure that electronic systems react correctly to various frequencies, just like ensuring that all strings on a guitar produce the right notes when played.
Reduction of Complexity
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
By reducing complex systems into manageable blocks, engineers can better understand and design systems with desired performance characteristics.
Detailed Explanation
Complex control systems can often be simplified by breaking them down into smaller, manageable blocks. This reduction process helps in focusing on specific interactions and relationships within the system. By analyzing these simpler components, engineers can ensure that the overall system meets desired performance requirements more easily and effectively.
Examples & Analogies
Consider a jigsaw puzzle: instead of trying to assemble the entire puzzle at once, itβs easier to group pieces by color or pattern first. Once you have smaller sections completed, you can work on connecting those groups to finish the whole picture. Similarly, by reducing a complex control system into simple blocks, engineers can piece together the components to achieve the desired functionality.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Block Diagrams: Important tools for visualizing control systems.
-
System Stability: A crucial aspect evaluated in both time and frequency domains.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
A block diagram can represent a feedback system, helping visualize how the output is connected back to the input.
-
Using Bode plots, engineers can evaluate how the gain and phase shift varies across frequencies.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
π΅ Rhymes Time
-
In a block diagramβs perfect frame, every component plays a crucial game.
π Fascinating Stories
-
Imagine all the parts of a machine, each represented in a block scene, working together to achieve the design team's dream.
π§ Other Memory Gems
-
Remember 'SPLAT' for key components: Signals, Plant, Loops, Analysis, Time.
π― Super Acronyms
BASICS - Block diagram Analysis for System Interconnections and Control Stability.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Block Diagram
Definition:
A visual representation of a system showing its components and the relationships between them.
-
Term: System Stability
Definition:
The ability of a system to maintain performance without oscillating or diverging.