Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take mock test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Hierarchical Clustering
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Today we will learn about hierarchical clustering, which is a fantastic way to group similar data points. Does anyone have an idea what clustering is?
I think clustering is putting similar data together, right?
Exactly! In hierarchical clustering, we create a tree structure called a dendrogram to visualize how data points are connected and grouped. This method can work in two ways: agglomerative and divisive.
What do those terms mean exactly?
Good question! Agglomerative means we start with individual data points and merge them into clusters, while divisive means we start with one big cluster and split it apart. Can anyone summarize what we've learned about the two types?
Agglomerative builds up clusters, and divisive breaks down a cluster!
Perfect summary! Let's remember this by using the acronym ‘A’ for Agglomerative and ‘D’ for Divisive. A for Assemble, D for Divide.
Linkage Criteria
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now, let’s talk about the different ways to define how we combine clusters using linkage criteria!
What is linkage exactly?
Linkage is the way we measure the distance between clusters. We have single linkage, complete linkage, and average linkage. What do you think single linkage does?
Maybe it measures the shortest distance between points?
That's right! Single linkage checks minimum distances, while complete linkage looks for the maximum distances. Average linkage? That averages the distances between points in clusters.
So, can we choose which one to use based on our data?
Exactly, depending on the dataset, one method might give us better insights. Remember: 'Small, Big, Average' for Single, Complete, and Average linkage!
Pros and Cons of Hierarchical Clustering
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Let’s evaluate the strengths and weaknesses of hierarchical clustering. What do you think is a benefit of using this method?
We don’t need to define the number of clusters beforehand?
Yes! That's a significant advantage because it allows us to explore the data structure without making assumptions about the number of clusters. What could be a disadvantage?
I’ve heard it can be very slow for large datasets?
Absolutely. Its computational intensity can make it impractical for large datasets. Always keep this in mind: 'Quick for small, Slow for Large!'
Practical Applications
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now, let's discuss where hierarchical clustering can be applied in the real world! Any thoughts?
How about in biological taxonomy? Classifying species?
Great example! It's used to group similar species based on traits. Can anyone think of another application?
Maybe in customer segmentation for marketing?
Excellent! Businesses can understand customer types and tailor strategies. ‘Clusters connect us!’ is a good way to remember these applications.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
Hierarchical clustering builds a hierarchy of clusters through either agglomerative or divisive methods. It uses different linkage criteria to measure distances between clusters, facilitating insights into data structure without pre-specifying the number of clusters.
Detailed
Hierarchical Clustering
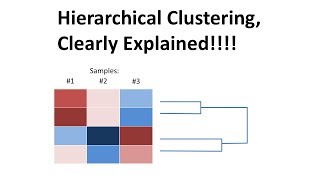
Hierarchical clustering is a powerful clustering technique that creates a tree-like structure called a dendrogram, which represents the relationships among data points or clusters. There are two primary approaches in hierarchical clustering: agglomerative (bottom-up) and divisive (top-down).
- Agglomerative Clustering starts with each data point as its own cluster and iteratively merges the closest pair of clusters until all points are contained within one single cluster. This approach is intuitive and commonly used, leading to a full hierarchy of clusters that can be explored at various levels of granularity.
- Divisive Clustering, on the other hand, begins with all data points in one cluster and recursively divides it into smaller clusters. This method is less commonly used due to its computational complexity.
In hierarchical clustering, linkages such as single linkage (minimum distance), complete linkage (maximum distance), and average linkage (average distance between points) determine how clusters merge. Proponents of hierarchical clustering favor it for its ability to produce a dendrogram that visually represents the data's hierarchical structure, aiding in understanding relationships within the data without prior knowledge of the optimal number of clusters. However, it is also computationally intense, making it less effective with large datasets.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Overview of Hierarchical Clustering
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
• Builds a tree (dendrogram) of clusters.
• Two approaches:
o Agglomerative (bottom-up): Each point starts as its own cluster, and pairs are merged.
o Divisive (top-down): Start with one cluster and recursively split it.
Detailed Explanation
Hierarchical clustering is a method that organizes data into a tree-like structure known as a dendrogram. There are two main approaches to this: Agglomerative and Divisive. In Agglomerative clustering, each data point begins as its own individual cluster. As the process continues, pairs of clusters are merged based on similarity, ultimately forming a single cluster that contains all points. On the other hand, Divisive clustering starts with one large cluster and progressively splits it into smaller and smaller clusters. This method allows for a detailed examination of the data's structure.
Examples & Analogies
Imagine a family tree, where the oldest ancestors are at the top, and their descendants branch out below. Each branch represents a small family group, just like how clusters branch out from the main cluster in hierarchical clustering.
Linkage Criteria
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Linkage Criteria:
• Single linkage: Minimum distance between points.
• Complete linkage: Maximum distance.
• Average linkage: Average pairwise distance.
Detailed Explanation
When performing hierarchical clustering, the way we define how clusters are formed and how distances are calculated is called 'linkage criteria'. There are three main types: Single linkage looks at the minimum distance between any two points in different clusters. Complete linkage considers the maximum distance between points in each cluster, ensuring that the clusters are more compact. Average linkage computes the average distance between all pairs of points in the clusters, balancing the approach between single and complete linkage. Each method can lead to different arrangements of the clusters.
Examples & Analogies
Think of a group of friends planning a reunion. If they decide the meeting point based on the nearest friend's home (single linkage), it might mean everyone has to travel a long distance from their homes. If they choose the furthest friend's home (complete linkage), it might create a venue that's very distant for most. Average linkage seeks to find a middle ground for everyone's convenience.
Pros and Cons of Hierarchical Clustering
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Pros:
• No need to specify number of clusters in advance.
• Good for hierarchical relationships.
Cons:
• Computationally intensive (O(n²) or more).
• Not suitable for very large datasets.
Detailed Explanation
One of the advantages of hierarchical clustering is that you don't need to decide the number of clusters beforehand; the data naturally suggests its clustering structure. This makes it particularly suitable for situations where you expect a hierarchical organization of data, such as family lineage or organizational structures. However, the method can be computationally expensive due to the need to calculate distances between all points, resulting in a complexity that can rise significantly with larger datasets. For very large datasets, this approach may take too long or require too much memory.
Examples & Analogies
Imagine you're organizing a conference with many speakers. Hierarchical clustering lets you discover how to group them by topics, without needing to pre-define how many panels to create. However, if you have hundreds of speakers, calculating all the possible groupings might become overwhelming, making the task impractical.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Agglomerative Clustering: Bottom-up method where each point starts as its own cluster.
-
Divisive Clustering: Top-down method that recursively divides one cluster into smaller ones.
-
Dendrogram: Visual representation of the clustering hierarchy.
-
Single Linkage: Merges clusters based on the minimum distance between points.
-
Complete Linkage: Merges clusters based on the maximum distance between points.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
In customer market research, hierarchical clustering identifies distinct customer segments based on purchasing behavior.
-
In biology, hierarchical clustering aids in categorizing species with similar genetic traits.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Agglomerate the small ones, split and divide, hierarchical clustering's your guide.
📖 Fascinating Stories
-
Imagine a librarian who starts with each book on its own shelf. Then they decide to group them by genre and create a library layout, forming clusters, without ever needing to count how many there would be in the end.
🧠 Other Memory Gems
-
Remember 'A for Assemble, D for Divide' to recall Agglomerative and Divisive Clustering.
🎯 Super Acronyms
For linkage methods
- 'S' for Single
- 'C' for Complete
- 'A' for Average. SCA.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Agglomerative Clustering
Definition:
A bottom-up approach to clustering that starts with each data point as its own cluster and merges them based on similarity.
-
Term: Divisive Clustering
Definition:
A top-down approach that starts with one cluster and recursively splits it into smaller clusters.
-
Term: Dendrogram
Definition:
A tree-like diagram that illustrates the arrangement of clusters based on their similarity.
-
Term: Linkage
Definition:
The method used to determine the distance between clusters in hierarchical clustering.
-
Term: Single Linkage
Definition:
A clustering method that considers the minimum distance between points in different clusters.
-
Term: Complete Linkage
Definition:
A clustering method that uses the maximum distance between points in different clusters.
-
Term: Average Linkage
Definition:
A clustering method that considers the average distance between points in different clusters.