Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to the Equation of Motion
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Today, we're going to explore the equation of motion for a single degree of freedom system. Can anyone tell me what the basic components of this equation are?
Is it mass, damping, and stiffness?
Correct! We have mass 'm', damping coefficient 'c', and stiffness 'k'. When we express this mathematically, we say, mx¨(t) + cx˙(t) + kx(t) = F(t). Does anyone know what F(t) represents?
It represents the external force acting on the system, right?
Exactly! Now, when we look at unit impulse input, that means F(t) can be represented as δ(t). Can anyone recall what δ(t) is?
Isn't it the Dirac delta function?
That's right! The Dirac delta function models an impulse as a force of very large magnitude acting over a very short period of time.
Understanding the System Response
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Next, let's look at how we can determine the system's response when we apply a unit impulse. When we substitute F(t) with δ(t), we get the equation mx¨(t) + cx˙(t) + kx(t) = δ(t). Why is this equation significant?
It shows how the system reacts immediately to the impulse!
Exactly! This equation reveals the system's core characteristics. If we solve it, we can derive what we call the impulse response function. Can anyone explain what an impulse response function signifies?
It describes how the system would respond over time to the immediate application of the impulse.
Spot on! The impulse response function is a fundamental concept in dynamic analysis, particularly in earthquake engineering.
Key Variables in SDOF Systems
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now let’s discuss the variables in our equation in more detail. Starting with mass 'm', why is mass an important factor in this context?
Mass affects how much the system will accelerate under an applied force?
Correct! Next, we have the damping coefficient 'c'. What role does damping play in our system?
It helps to reduce the oscillations and brings the system back to rest more quickly, right?
Right again! Damping is crucial for understanding how energy is dissipated in the system. Finally, what about stiffness 'k'?
Stiffness determines how resistant the system is to deformation!
Exactly! All these variables together help us characterize the system's response to any applied input.
Implications in Earthquake Engineering
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
In what ways can the equation of motion for SDOF systems be useful in earthquake engineering?
It helps predict how buildings will behave when seismic forces act upon them.
Correct! Understanding the impulse response helps in designing structures that can withstand sudden excitations. What else can we derive from the impulse response function?
We can evaluate the performance of structural control systems based on how they respond to impulsive forces.
Exactly! Hence, mastering the application of these equations is vital for engineers involved in structural design.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The equation of motion for a linear SDOF system is discussed in relation to how the system responds to an applied force, particularly highlighting the form when subjected to a unit impulse. The section outlines mass, damping, stiffness, displacement, and external force variables, ultimately guiding towards deriving the impulse response function.
Detailed
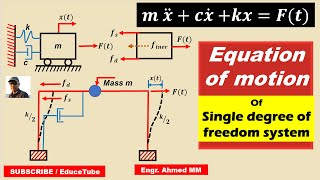
In this section, we focus on the equation of motion for a single degree of freedom (SDOF) system, described mathematically by the equation: mx¨(t) + cx˙(t) + kx(t) = F(t). Here, 'm' denotes the mass, 'c' represents the damping coefficient, 'k' indicates stiffness, 'x(t)' stands for the displacement, and 'F(t)' is the external force applied. When this external force is a unit impulse represented by F(t) = δ(t), the equation simplifies to mx¨(t) + cx˙(t) + kx(t) = δ(t). Solving this equation allows us to derive the impulse response function of the system, an essential tool in dynamic analysis and structural response predictions, particularly in fields such as earthquake engineering.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Basic Equation of Motion
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
For a linear SDOF system subjected to a force F(t), the equation of motion is:
mx¨(t) + cx˙(t) + kx(t) = F(t)
Where:
• m: Mass
• c: Damping coefficient
• k: Stiffness
• x(t): Displacement
• F(t): External force (here, impulse)
Detailed Explanation
In this equation, we describe how a single degree of freedom system behaves when a force is applied. The left side of the equation consists of three terms that represent: the inertia (mx¨(t)), damping (cx˙(t)), and stiffness (kx(t)). The right side shows the external force that is acting on the system, which can vary over time. Essentially, this equation serves as a balance between the forces acting on the mass and the forces exerted by the system due to its characteristics.
Examples & Analogies
Imagine a swing (which lets us think of a mass hanging by a rope) as our SDOF system. When you push the swing (applying an external force), it starts moving (displacement). The swing also has resistance to motion due to air and friction at the pivot (damping) and will want to return to its resting position if displaced (stiffness), which can be thought of like a spring pulling back.
Special Case of Unit Impulse
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
For unit impulse input: F(t) = δ(t) So, the governing equation becomes: mx¨(t) + cx˙(t) + kx(t) = δ(t)
Detailed Explanation
Here, we introduce the concept of a unit impulse, represented by δ(t). This is a mathematical construct useful for analyzing responses of systems. When we substitute this impulse into our equation, it transforms our system’s behavior into one that can reveal essential dynamic characteristics. The idea here is that a unit impulse suddenly applies a force to the system, and the response we observe helps us understand how the system reacts to rapid applications of force.
Examples & Analogies
Think about hitting a punching bag lightly. That sudden force is like our unit impulse. The bag suddenly compresses (the force is applied), and then it swings back due to its structure and materials (the system's reaction). By studying how far and fast it moves, we understand the dynamics of the punching bag — which parallels how engineers study other systems under impulsive forces.
Impulse Response Function
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Solving this equation gives the impulse response function of the system.
Detailed Explanation
The impulse response function is a critical aspect of this analysis. It essentially tells us how the system will respond over time to the initial impulse. After applying the mathematical methods to solve the governing equation with the unit impulse, we can gain insights into how the system behaves in the short and long term. This response gives engineers vital information for ensuring safety and performance in real structures.
Examples & Analogies
Consider how a pebble thrown into a pond creates ripples. The first ripple represents the initial impact (the impulse), while the subsequent ripples show how the water (our system) responds to that single input. The pattern of those ripples—including how quickly they fade—can tell us everything about the pond's shape and depth, much like how the impulse response function informs engineers about the structural behavior.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Equation of Motion: mx¨(t) + cx˙(t) + kx(t) = F(t). Describes the relationship between mass, damping, stiffness, and external force.
-
Unit Impulse: F(t) = δ(t). Represents the application of a momentary force in the analysis.
-
Impulse Response Function: Derives from the equation of motion and reflects the system's response to an impulse.
-
Damping: Influences how quickly the oscillations reduce over time.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
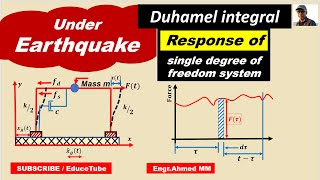
An SDOF building responding to an earthquake can be modeled as an SDOF system where the equation of motion reflects the forces due to inertia, damping, and stiffness.
-
In earthquake-resistant design, impulse response functions help predict how a building structure will react to seismic impulses.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
M is for mass and C is for calm, K for stiffness holds the system's palm.
📖 Fascinating Stories
-
Imagine a tall building swaying gently like a tree in the wind; the m (mass) grounds it while c (damping) ensures it doesn't sway too wildly.
🧠 Other Memory Gems
-
To remember the variables m, c, k: 'My Cool Kinetic system'.
🎯 Super Acronyms
Use MCD for Mass, C for Damping, and K for Stiffness.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Impulse
Definition:
A force of very large magnitude acting over a very short period of time, typically modeled by the Dirac delta function.
-
Term: Dirac Delta Function
Definition:
A mathematical representation of an impulse used in signal processing and physics, denoted as δ(t).
-
Term: Single Degree of Freedom (SDOF)
Definition:
A system that has only one independent motion or vibration mode.
-
Term: Impulse Response Function
Definition:
The output of a system when subjected to a unit impulse input; a crucial concept in dynamic analysis.
-
Term: Damping Coefficient
Definition:
A parameter that quantifies the damping effect in a system, indicating how quickly oscillations decay.
-
Term: Stiffness
Definition:
A measure of a structure's resistance to deformation when subjected to an applied force.