Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Green’s Function
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Today, we will discuss the impulse response function, commonly known as Green's function. This function is crucial in understanding how systems react to applied forces.
What do we mean by a unit impulse input?
A unit impulse input, represented by δ(t), is a mathematical function that models an instantaneous force applied at a single point in time, allowing us to analyze the system's immediate response. Can anyone describe the impact of such an impulse on a structure?
I think it would cause an immediate reaction that can be tracked over time.
Exactly! And understanding this immediate reaction helps us predict future behavior under various inputs.
Does this mean we can observe the entire system behavior just from one impulse?
Yes, precisely! This is the essence of using convolution in response analysis.
So if we know h(t), we can find out how the system reacts to any force F(t)?
Correct! That's why h(t), the impulse response, is fundamental.
In summary, Green's function gives us a powerful way to analyze and predict system behavior, which is essential in fields like earthquake engineering.
Mathematical Representation of Impulse Response
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
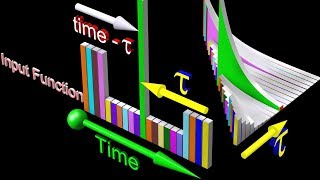
Let’s look at the mathematical representation of the impulse response function. We define the system response as follows: \[ x(t) = \int_{0}^{t} h(t - \tau) F(\tau) d\tau \].
Can you explain what the variables mean in this equation?
Sure! In this formula, x(t) is the total response at time t, h(t - τ) is the impulse response function, and F(τ) represents the external force applied at time τ. This integral sums up all effects over time.
What happens if F(t) is another impulse function?
Good question! If F(t) is another impulse function, the total response will reflect the combined effects, allowing us to analyze more complex excitations.
Is it true that knowing h(t) simplifies our calculations?
Absolutely! It allows us to compute responses with various external forces efficiently. Remember, if we understand the initial condition from an impulse, we can analyze the entire system.
In summary, the impulse response function is a powerful tool that enables us to predict future behavior using past responses.
Applications of Impulse Response in Engineering
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now that we understand the theory, let's discuss some practical applications of impulse response functions in engineering.
Can you give an example of where this is particularly useful?
Certainly! In earthquake engineering, ground motions can be approximated as sequences of impulses. By understanding how structures respond to these impulses, we can design better buildings that withstand seismic activities.
That sounds important! What about system identification?
Great point! Impulse response functions help determine system parameters from real measured response data. This is essential for creating accurate models.
Are there applications in monitoring structural health?
Indeed! By measuring how structures respond to impulse tests, we can assess their condition and performance over time.
In summary, understanding the impulse response is vital for designing and assessing structures in earthquake engineering and beyond.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section explains how the impulse response function can be used to analyze the response of linear time-invariant systems to any external force through convolution. Understanding this function is crucial in various engineering applications, especially in earthquake engineering where impulse-like forces are common.
Detailed
Detailed Summary
The impulse response function, often referred to as Green’s function, is a fundamental concept in dynamic systems analysis, particularly within the context of linear time-invariant (LTI) systems. It defines the reaction of such systems to a unit impulse input, mathematically denoted as δ(t). In operational terms, once the impulse response function h(t) of a system is established, it can be utilized to predict the system's response to any arbitrary input force F(t) through the convolution integral:
\[ x(t) = \int_{0}^{t} h(t - \tau) F(\tau) d\tau \]
This equation indicates that the total response x(t) at time t can be perceived as the accumulation of responses to infinitesimally small impulses applied at earlier times. This characterizes the richness of dynamic responses resulting from varying external forces, crucial in applications like earthquake engineering, where ground motions are treated as sequences of impulsive forces. By mastering the impulse response function, engineers can effectively anticipate how structures react under sudden excitations.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Definition of Impulse Response Function
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The impulse response function, also called Green’s function h(t), is defined as the response of a system to a unit impulse input δ(t).
Detailed Explanation
The impulse response function, commonly referred to as Green's function, represents how a dynamic system reacts when subjected to a direct, instantaneous force known as a unit impulse. In mathematical terms, a unit impulse can be represented by the Dirac delta function, denoted as δ(t). When we apply this impulse to a system, the output we observe over time is captured by the impulse response function, h(t). This is foundational in understanding how systems behave under sudden inputs.
Examples & Analogies
Imagine striking a bell with a hammer. The sound it produces is the system’s impulse response to the sharp, short impact (the impulse). Just as different bells resonate uniquely based on their shape and material, different systems will have their own impulse response functions, which describe how they respond to forces applied suddenly.
Convolution with a General Input
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
For a linear time-invariant system, the total response to any arbitrary force F(t) can be obtained using convolution:
\[ x(t)= \int_{0}^{t} h(t-\tau)F(\tau)d\tau \]
Detailed Explanation
In linear time-invariant (LTI) systems, if we know how the system responds to a unit impulse (h(t)), we can predict its behavior in response to any arbitrary external force F(t) using a mathematical operation called convolution. The convolution integral sums the effects of all past inputs (forces) on the current system output at time t. It effectively combines the history of the force inputs with the system’s impulse response, resulting in the total output of the system over time.
Examples & Analogies
Think of a sponge soaked in water. If you press the sponge (the impulse) to squeeze out some water, the response of the sponge reflects how much water is released from it in reaction to your force (the output). Now consider if you had a melted ice cube (the force applied over time) instead of a single squeeze; how much liquid you get out will depend on both the sponge's characteristics and how hard and how long you press on it – this is similar to how convolution works in determining the total response based on various inputs.
Importance of Knowing h(t)
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Thus, knowing h(t) allows us to determine system response to any general input.
Detailed Explanation
Understanding the function h(t) is crucial because it serves as a key that unlocks the behavior of the system under various loading conditions. Once we have this function, we can easily calculate how the system will respond not just to a single impulse but to any complex, time-varying loads by applying convolution. This is particularly valuable in engineering applications where structures must be designed to withstand dynamic forces, such as earthquakes.
Examples & Analogies
Think of h(t) as a recipe for baking a cake. If you know the recipe (the impulse response), you can adjust your ingredients (the input forces) and cooking times to achieve different flavors or textures (the system response) in the final cake. Just as having the right recipe lets you create various cakes, knowing the impulse response enables engineers to predict how structures will behave under different real-world conditions.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Impulse Response Function: A mathematical representation of how a system responds to a unit impulse input.
-
Convolution: A technique used to find the output of a system given an input signal and the system's impulse response.
-
Applications in Earthquake Engineering: Understanding impulse response helps in designing structures that can resist repetitive seismic forces.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
In earthquake engineering, the ground's accelerations can be modeled as a series of unit impulses, allowing engineers to apply the impulse response function to determine structural behavior during seismic events.
-
When analyzing a structure's dynamic response, engineers can use impulse testing to measure its impulse response function experimentally, assisting in system identification and performance evaluation.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
When structures feel a quick attack, Green's function shows how they bounce back.
📖 Fascinating Stories
-
Imagine an engineer watching a wave spread from where a pebble dropped in water. Each ripple shows the response to that small, sudden force, just like how Green's function helps us visualize systems reacting to impulses.
🧠 Other Memory Gems
-
Remember 'CIRCUIT' for Convolution: Combine Inputs Responsively, Calculate Unit Response In Time.
🎯 Super Acronyms
H.E.L.P. - Hammer for Impulse, Evaluate Linear Parameters.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Impulse Response Function (Green's Function)
Definition:
A mathematical function that describes the output or response of a linear time-invariant system when presented with a unit impulse input.
-
Term: Convolution
Definition:
A mathematical operation used to express the total response of a system to an arbitrary input as the integral of the product of the input function and the impulse response function.
-
Term: Unit Impulse
Definition:
A fundamental concept in systems theory where a force is applied instantaneously at a specific point in time, modeled as the Dirac delta function.
-
Term: Linear TimeInvariant (LTI) System
Definition:
A type of system where the governing equations are linear and the system's parameters do not change over time.