Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Impulse Forces
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Today, we're going to explore impulse forces, which are defined as forces of very large magnitude acting over a very short period. Can anyone explain what this means?
Does it mean that impulse forces are very powerful but brief?
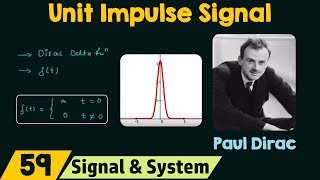
Exactly! And mathematically, we use the Dirac delta function, denoted as δ(t), to represent this idea. This function is crucial for analyzing responses due to such forces.
What's special about the Dirac delta function?
Great question! The Dirac delta function is 0 for all values except t = 0, where it takes on a theoretically infinite value. When integrated over time, it equals one, which is key in finding system responses.
So, it helps us understand how a system behaves instantly when impacted?
Precisely! This sifting property allows us to test dynamic behaviors at an instant. Let’s summarize: Impulse forces are strong but concise, mathematically represented by δ(t), crucial for defining system responses.
Equations of Motion
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now let's move on to how we formulate the equations of motion for an SDOF system when subjected to an impulse. Can anyone recall the general form of Newton's second law?
Is it F = ma?
That's right! We can express the equation of motion as mx¨(t) + cx˙(t) + kx(t) = F(t). For a unit impulse, we set F(t) to δ(t). Thus, our specific equation becomes mx¨(t) + cx˙(t) + kx(t) = δ(t).
Why do we use 'm', 'c', and 'k' in the equation?
Good question! Here, 'm' represents mass, 'c' is the damping coefficient, and 'k' is the stiffness of the system. These parameters significantly affect how the system will respond to impulses.
So, the solution to this equation tells us how the structure reacts over time?
Exactly! The solution gives us the impulse response function crucial for predicting the system’s dynamic behavior.
Free Vibration Response
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Let’s dive into how an undamped SDOF system behaves when an impulse is applied. Who can remind me what happens in this scenario?
The system oscillates without any damping effect, right?
Yes! The governing equation simplifies to mx¨(t) + kx(t) = δ(t). For our undamped free vibration response, we derive x(t) = sin(ωnt), where ωn is the natural frequency. Can someone tell me why this is important?
It shows us how the system’s natural properties affect its response to impulses!
Exactly! And when we include damping, we introduce decay into the oscillation. The response becomes x(t) = e^(-ζωnt)sin(ωdt). What does this damping tell us about real-world applications?
It helps reduce oscillations over time, which is crucial in structure design!
Well put! Damping is vital in earthquake engineering to ensure structures absorb shocks effectively.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section introduces impulse forces defined by the Dirac delta function, and explains the equations of motion for single degree of freedom (SDOF) systems under unit impulse. It discusses both damped and undamped systems, emphasizing the significance of the impulse response function in structural analysis and earthquake engineering.
Detailed
Impulse and Response to Unit Impulse
This section addresses the characteristics of impulse forces and their mathematical representation using the Dirac delta function. An impulse is defined as a high-magnitude force acting over an infinitesimally short time, leading to a sharp response in dynamic systems. The mathematical representation is framed within the context of linear time-invariant (LTI) systems, with key equations defining the system's motion under impulsive loads. It delves into:
9.1 Impulse Force and its Mathematical Representation
The impulse is mathematically represented by integrating the force over time, emphasizing the sifting property of the Dirac delta function, which allows analysis of system responses at an instant.
9.2 Equation of Motion for SDOF System
The governing equation for a linear SDOF system under an impulse input is presented, showing how to derive the impulse response, vital for predicting dynamic behavior under seismic events.
9.3 Free Vibration Response of Undamped SDOF System
This subtopic looks at the response of an undamped SDOF system, showcasing the integral of motion under a unit impulse and introducing natural frequencies defined by system parameters.
9.4 Response of Damped SDOF System
It emphasizes the effects of damping in response functions, analyzing how decay in oscillations occurs in underdamped systems.
9.5 Unit Impulse Response Function
This important concept explains how the impulse response function allows prediction of a system's response to any force applied via convolution principles.
9.6 Physical Interpretation in Earthquake Engineering
The significance of these concepts in earthquake engineering is underscored, especially how they help in constructing response histories and designing resilient structures.
9.7 Numerical Example
A practical example illustrates the calculation of impulse response parameters for a given system.
9.12 Importance in Seismic Design and Analysis
The chapter concludes with applications of impulse response analysis in time-history simulation and seismic design evaluations.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Understanding Impulse Force
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
An impulse is defined as a force of very large magnitude acting over a very short period of time. Theoretically, this is modeled by the Dirac delta function, denoted as δ(t). The mathematical impulse I applied over a time interval t to t1 is:
\[ I = \int_{t_1}^{t_2} F(t) dt \]
For a unit impulse, this simplifies to:
\[ \int_{-\infty}^{\infty} δ(t) dt = 1 \]
Detailed Explanation
An impulse is a force applied suddenly and briefly. In mathematics, we often represent this using the Dirac delta function, which is a way to express an infinitely large force over an infinitesimally small duration. The integral of the Dirac delta function over its entire range equals one, which signifies that the total effect of impulse is captured, even though the force acts only momentarily.
Examples & Analogies
Think of an impulse as a quick jab. It’s like tapping a friend on the shoulder really hard for just a moment. Even though the tap is quick, it gets your friend's attention immediately, similar to how an impulse force can cause instant reactions in structures.
Equations of Motion for SDOF Systems
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
For a linear SDOF system subjected to a force F(t), the equation of motion is:
\[ mx¨(t) + cx˙(t) + kx(t) = F(t) \]
For unit impulse input: F(t) = δ(t)
So, the governing equation becomes:
\[ mx¨(t) + cx˙(t) + kx(t) = δ(t) \]
Detailed Explanation
The motion of a single degree of freedom (SDOF) system can be described by a second-order differential equation that considers mass, damping, and stiffness. When we apply a unit impulse as the external force, we adjust the equation to reflect this specific force input, allowing us to derive the system's response to the impulse.
Examples & Analogies
Imagine a swing (the SDOF system). If you push it lightly and then suddenly give it a strong push (the impulse), you can analyze how far and how fast it swings based on the swing's weight (mass), how much it wants to swing back and forth (stiffness), and how much it slows down (damping).
Response of Undamped SDOF System
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
When damping c=0, the equation simplifies to:
\[ mx¨(t) + kx(t) = δ(t) \]
Let ω = \sqrt{\frac{k}{m}} be the natural frequency.
Initial conditions just before impulse:
• x(0−)=0
• x˙(0−)=0
Integrating the equation over a small interval around t=0:
\[ \int_{0^-}^{0^+} mx¨(t) dt + \int_{0^-}^{0^+} kx(t) dt = \int_{0^-}^{0^+} δ(t) dt \]
Then, the free vibration response for t>0:
\[ x(t) = \frac{1}{mω_n} sin(ω_n t) \]
Detailed Explanation
In an undamped system, we focus simply on the mass and stiffness without considering any damping effects. The resulting response can be modeled as a sine wave that reflects how the system will oscillate in response to the impulse force. The natural frequency determines the speed of oscillation and the amplitude is influenced by the magnitude of the impulse.
Examples & Analogies
Think of a child on a swing. If you give them a push (an impulse) with no one holding them back (no damping), they'll swing back and forth indefinitely until fatigue from air resistance slows them down. Their motion can be described as a smooth back-and-forth swinging motion, akin to the sine wave response.
Response of Damped SDOF System to Unit Impulse
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
For a damped system, the equation of motion is:
\[ mx¨(t) + cx˙(t) + kx(t) = δ(t) \]
Let:
• ζ = \sqrt{\frac{c}{2 km}} be the damping ratio
• ω_n = \sqrt{\frac{k}{m}} be the natural frequency
• ω_d = ω_n \sqrt{1−ζ^2}, the damped natural frequency.
Assuming initial conditions:
• x(0−)=0, x˙(0−)=0
• x˙(0+)= \frac{1}{m}
Then for ζ <1 (underdamped case):
\[ x(t) = \frac{1}{mω_d} e^{-ζω_nt}sin(ω_d t), \ t>0 \]
Detailed Explanation
In systems with damping, the response not only oscillates but also decreases in amplitude over time due to energy loss from effects like friction or air resistance. This equation captures the response of a damped system to an impulse by introducing a decay term that reflects the damping influence. The damped frequency shows how the system's motion slows down more than an undamped system would.
Examples & Analogies
Consider a vibrating guitar string. When plucked (an impulse), it vibrates rapidly but dampens down (loses energy) over time. Each time the string vibrates, it produces sound, but as the energy dissipates through air (like the damping in our equation), the sound fades instead of ringing indefinitely.
Green’s Function and System Response
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
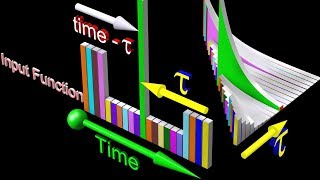
The impulse response function, also called Green’s function h(t), is defined as the response of a system to a unit impulse input δ(t).
For a linear time-invariant system, the total response to any arbitrary force F(t) can be obtained using convolution:
\[ x(t) = \int_{0}^{t} h(t−τ) F(τ) dτ \]
Detailed Explanation
Green's function acts as a tool in system analysis, revealing how a system reacts to impulsive forces. Using convolution, we can take the impulse response function and apply it to any force by integrating over time, merging the system's response to many small impulses into one complete response. This principle allows engineers to predict how structures react to more complex loading conditions beyond just simple impulses.
Examples & Analogies
Think of making a smoothie (the response) where you add various ingredients (the forces) one at a time. The final taste is influenced by all the ingredients combined, just like the total response of a system depends on the individual impulses applied over time.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Impulse Forces: Sudden forces of short duration modeled by the Dirac delta function, essential for analyzing dynamic systems.
-
Impulse Response Function: Describes how systems respond to a unit impulse, crucial for predicting behaviors under seismic loads.
-
Free Vibration: The response characteristics of a system when allowed to oscillate freely after an impulse, noting the effects of damping.
-
Damping: The process of energy dissipation in oscillating systems, leading to a reduction in amplitude over time.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
A bridge subjected to an impulsive force due to a sudden earthquake can be modeled using impulse equations to predict its reaction.
-
An undamped pendulum impacted by a quick force can be analyzed through its natural frequency to determine the future oscillations.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
An impulse spike is quick and bright, causing systems to respond in flight.
📖 Fascinating Stories
-
Imagine a soldier throwing a grenade (impulse). When it explodes, the blast hits the wall quickly (Dirac delta function) and the wall shakes (system response).
🧠 Other Memory Gems
-
Remember SDOF as 'Single Dynamic Order of Freedom' to capture its essence in dynamics.
🎯 Super Acronyms
NATURE - Natural frequency, Amplitude, dUmping ratio, Tranquil response, when External forces act.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Impulse
Definition:
A force of very large magnitude acting over a very short period of time, mathematically modeled by the Dirac delta function.
-
Term: Dirac Delta Function (δ(t))
Definition:
A mathematical function that represents an impulse, defined as being zero everywhere except at one point, where it integrates to one.
-
Term: Single Degree of Freedom (SDOF)
Definition:
A dynamic system that can be described by a single coordinate, often used in structural analysis.
-
Term: Natural Frequency (ωn)
Definition:
The frequency at which a system oscillates when not subjected to external forces nor damping.
-
Term: Damping Ratio (ζ)
Definition:
A dimensionless measure describing how oscillations in a system decay after a disturbance.