Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Mode Shape Computation
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Welcome, everyone! Today, we are going to dive into the computation of mode shapes. Can any of you explain what a mode shape is?
Isn't it the shape a structure takes during vibration?
Exactly! A mode shape describes how a structure deforms at specific natural frequencies. Now, why do you think it's important to compute mode shapes?
It helps in understanding how buildings respond to earthquakes, right?
Correct! By understanding mode shapes, we can design better structures that can withstand seismic forces. Let’s get into how we compute these shapes.
Methods for Computation
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
There are several methods to compute mode shapes. Who can name a few?
I remember you mentioning analytical methods for small systems.
And numerical methods for larger systems!
Great! Analytical methods are indeed suitable for systems with fewer degrees of freedom. For larger structures, we often use numerical methods like the subspace iteration and the Lanczos algorithm. Can anyone tell me what the Rayleigh-Ritz method is?
Is it used to approximate the mode shapes?
Yes! It helps in simplifying complex problems. Also, when dealing with intricate structures, we often use software tools, such as SAP2000 or ANSYS, which makes the task much easier.
Importance of Software in Computation
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Why do you think software is crucial for computing mode shapes in high-rise buildings?
Because they can handle complex calculations faster?
Exactly! Software like ETABS can analyze complex systems much quicker than manual calculations. It factors in various loads and conditions that influence mode shapes. Can you think of an example of a structure where this could be essential?
Maybe a skyscraper during an earthquake?
Absolutely! Computational tools are vital in ensuring these structures are safe during seismic events. Let’s summarize today’s discussions.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The computation of mode shapes is crucial in structural dynamics, involving analytical methods for simpler systems and numerical techniques like subspace iteration for larger structures. The use of software tools for computations is emphasized for high-rise buildings.
Detailed
In the study of mode shapes, particularly within the context of structural dynamics and earthquake engineering, this section focuses on techniques for their computation. Mode shapes are integral to understanding how structures will react under dynamic conditions.
- Methods of Computation: Mode shapes can be derived using variations in approaches:
- Analytical Methods: These are suitable for small systems, particularly those with 2 or 3 degrees of freedom (DOF).
- Numerical Methods: For larger and more complex systems, numerical approaches are essential. Important algorithms include:
- Subspace Iteration
- Lanczos Algorithm
- Rayleigh-Ritz Method
- For intricate structures, using software such as SAP2000, ETABS, or ANSYS is recommended to facilitate accurate calculations.
- Importance in Engineering: Understanding how to compute mode shapes is vital for engineers involved in designing earthquake-resistant structures, ensuring resonance and amplified motions do not lead to structural failure.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Methods for Computing Mode Shapes
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Mode shapes can be computed by solving the eigenvalue problem using:
- Analytical methods for small systems (e.g., 2-DOF, 3-DOF)
- Numerical methods for large systems using:
- Subspace iteration
- Lanczos algorithm
- Rayleigh-Ritz method
For high-rise or complex structures, software like SAP2000, ETABS, or ANSYS is commonly used.
Detailed Explanation
To compute mode shapes, engineers can use either analytical methods or numerical methods. Analytical methods work best for smaller systems, such as those with two or three degrees of freedom (2-DOF, 3-DOF). For larger, more complex systems, numerical methods, which include subspace iteration, the Lanczos algorithm, and the Rayleigh-Ritz method, become necessary. Furthermore, when dealing with very large structures like high-rise buildings, specialized software such as SAP2000, ETABS, or ANSYS provides tools to carry out these calculations efficiently.
Examples & Analogies
Think of calculating mode shapes like solving different types of puzzles. For small, simple puzzles like those with just a few pieces, you might solve them by hand. However, for intricate puzzles with many pieces, like a complex 1000-piece jigsaw, you would likely use special software that can aid in piecing it together quickly, just like engineers use software to compute mode shapes for large structures.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Analytical Methods: Techniques suitable for smaller systems to compute mode shapes.
-
Numerical Methods: Algorithms like subspace iteration and Lanczos algorithm used for larger systems.
-
Software Tools: Applications like SAP2000 and ANSYS greatly assist in the computation of complex mode shapes.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
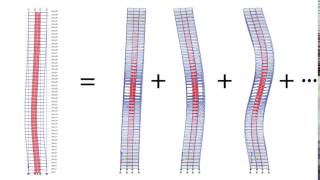
For a 3-DOF shear building, three distinct mode shapes will exist, each representing a different displacement profile across the floors.
-
In a cantilever beam, the first mode shape exhibits a single curvature while the second mode shows a double curvature.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Mode shape patterns sway and dance, during vibrations they take a chance.
📖 Fascinating Stories
-
Imagine a tree in the wind, swaying back and forth - that deformation pattern is like a mode shape, showing how it moves at different 'frequencies' of the wind.
🧠 Other Memory Gems
-
AN = Analyze Numerically to remember Analytical and Numerical methods for mode shapes.
🎯 Super Acronyms
MATH = Mode shapes, Analytical methods, Techniques, Harmonics.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Mode Shape
Definition:
The deformation pattern a structure exhibits at a specific natural frequency during free vibration.
-
Term: Natural Frequency
Definition:
The frequency at which a system tends to oscillate in the absence of external forces.
-
Term: Degrees of Freedom (DOF)
Definition:
The number of independent movements a system can undergo.
-
Term: Eigenvalue Problem
Definition:
A mathematical formulation used to determine the natural frequencies and mode shapes of a system.