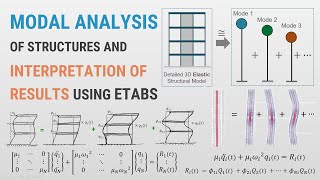
Mode Shapes
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Mode Shapes
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Welcome everyone! Today we will begin our exploration of mode shapes. Can anyone tell me what a mode shape represents in structural dynamics?

Is it the shape that a structure takes when it vibrates?

Exactly! A mode shape is indeed the deformation pattern of a structure at a specific natural frequency during free vibration. How does free vibration differ from forced vibration?

Free vibration occurs without external force after an initial disturbance, while forced vibration happens with continued external inputs.

Well said! Now, why do you think understanding these mode shapes is important for engineers?

It helps in designing structures that can withstand earthquakes and avoid resonance!

Correct! Resonance can lead to catastrophic failures, so we must analyze these mode shapes carefully during the design process.

I find it interesting that you mentioned that resonance can cause failure. Does that mean different buildings can have different mode shapes?

Absolutely! Each structure has its unique modes of vibration based on its design, material, and geometry. Let's keep that in mind as we delve deeper into this topic.
Mathematical Formulation of Mode Shapes
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Moving on, let's talk about the mathematical formulation of mode shapes. We use matrices to describe these systems. Can anyone explain the relationship between mass and stiffness in a harmonic motion system?

I think we use the mass and stiffness matrices to describe how the system vibrates.

Exactly! This leads to the eigenvalue problem. If we consider the equation [M]{u¨} + [K]{u} = {0}, we can find mode shapes by substituting a harmonic solution. Who can recall what we get when we rewrite this equation?

I remember that it becomes ([K] − ω²[M]){ϕ} = {0}.

Well done! And from this, what do {ϕ} and ω represent?

{ϕ} is the mode shape, and ω is the natural frequency.

That's correct! Understanding this formulation allows us to calculate the natural frequencies and corresponding mode shapes necessary for assessing structure response.
Properties of Mode Shapes
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now, let's discuss some properties of mode shapes, particularly orthogonality. Can anyone tell me what orthogonality means in this context?

Is it about the mode shapes being independent of each other?

Great insight! Mode shapes are orthogonal with respect to both the mass and stiffness matrices. Can anyone recall the equations for mass and stiffness orthogonality?

For mass orthogonality, it's {ϕ}^T[M]{ϕ} = 0 for i≠j, and for stiffness, {ϕ}^T[K]{ϕ} = 0 for i≠j!

Exact! Orthogonality is crucial for modal superposition. Now why might we want to normalize these mode shapes?

It simplifies analysis by making calculations easier and ensures they are consistent.

Yes! Normalization methods help in clarity during analysis, especially during response spectrum and time history evaluations.
Computation and Interpretation of Mode Shapes
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Let's look at the computation of mode shapes now. What methods can we use to solve the eigenvalue problem for larger systems?

We can use numerical methods like subspace iteration, Lanczos algorithm, and Rayleigh-Ritz method.

Correct! And for practical applications, what software do we typically utilize?

SAP2000, ETABS, and ANSYS are commonly used for complex structures.

Exactly! Understanding these tools helps us compute mode shapes efficiently. Now, how can we interpret the first mode shape compared to higher mode shapes?

The first mode shape generally represents global movement, while higher modes show localized or complex behaviors.

Perfect! Each mode shape plays a significant role in evaluating the dynamic response of structures.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
Understanding mode shapes is fundamental in earthquake engineering as they depict how structures deform at specific natural frequencies during free vibration. This section discusses the derivation, properties such as orthogonality and normalization, computational techniques, and their crucial roles in modal analysis and seismic design.
Detailed
Mode Shapes in Earthquake Engineering
In the context of earthquake engineering and structural dynamics, mode shapes are the characteristic deformation patterns that structures exhibit at specific natural frequencies during free vibration. These shapes are essential for understanding how structures respond dynamically to external forces, particularly seismic activities. In this chapter, we cover:
- Free Vibration: The dynamics of multi-degree-of-freedom systems showcasing various mode shapes corresponding to unique natural frequencies.
- Mathematical Formulation: The derivation of mode shapes through equations governing mass and stiffness, leading to the eigenvalue problem.
- Properties: Discussing orthogonality concerning mass and stiffness matrices, and normalization techniques for analytical convenience.
- Computation: Methods for calculating mode shapes, from analytical approaches for simpler systems to numerical methods for large structures using advanced algorithms and software.
- Interpretation and Application: Examining how different mode shapes behave in various structures, their significance in seismic design, and their role in optimizing structural integrity through modal participation factors and response analysis.
Each of these components underlines the crucial role that mode shapes play in the field of structural engineering, particularly in designing safer buildings against seismic threats.
Youtube Videos






Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Mode Shapes
Chapter 1 of 8
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
In the context of earthquake engineering and structural dynamics, mode shapes represent the characteristic deformation patterns that structures undergo at specific natural frequencies during free vibration. These shapes provide vital insights into how structures respond dynamically and are central to modal analysis — a core concept in evaluating seismic behavior. Understanding mode shapes is crucial for designing earthquake-resistant structures and ensuring that resonance or amplified motions do not result in catastrophic failure.
Detailed Explanation
Mode shapes are defined as the specific patterns of deformation that structures exhibit when they vibrate freely at their natural frequencies. These patterns help engineers understand how structures behave during events like earthquakes which can severely impact their stability. By analyzing mode shapes, engineers can design structures that withstand seismic forces and avoid potential failures.
Examples & Analogies
Think of a swing. When you push it gently, it moves back and forth in a certain way that depends on its shape and the force applied. Similarly, when buildings experience natural forces like earthquakes, they have characteristic patterns, or mode shapes, that dictate how they move and react.
Free Vibration and Mode Shapes
Chapter 2 of 8
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
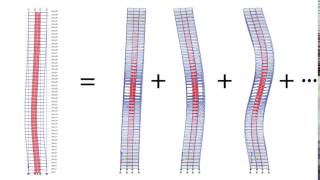
Free vibration refers to the vibration of a system without any external force, after an initial disturbance. In multi-degree-of-freedom (MDOF) systems, the vibration response is a combination of several independent modes of vibration, each with a unique natural frequency and mode shape.
• Definition: A mode shape is the deformation pattern of a structure at a specific natural frequency during free vibration.
• Each mode shape corresponds to one natural frequency.
• The number of possible mode shapes is equal to the number of degrees of freedom (DOFs) in the system.
Example: For a 3-DOF shear building, three distinct mode shapes will exist, each representing a different vertical displacement profile across the floors.
Detailed Explanation
Free vibration occurs when a system vibrates solely from an initial push or disturbance, without any further external forces acting on it. In buildings with multiple degrees of freedom (like many engineering structures), the total vibration response is made up of several modes. Each mode shape represents how the structure deforms at a specific natural frequency, and the count of these mode shapes equals the count of degrees of freedom the structure has.
Examples & Analogies
Imagine a guitar string. When plucked, it vibrates in multiple ways depending on where it was plucked and its structure, creating different musical notes. In a similar way, buildings vibrate in specific patterns (mode shapes) when they are disturbed.
Mathematical Formulation of Mode Shapes
Chapter 3 of 8
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Consider an undamped linear MDOF system governed by:
[M]{u¨}+[K]{u}={0}
Where:
• [M] = Mass matrix
• [K] = Stiffness matrix
• {u} = Displacement vector
Assuming a harmonic solution of the form:
{u(t)}={ϕ}sin(ωt)
Substituting and simplifying leads to the eigenvalue problem:
([K]−ω²[M]){ϕ}={0}
• ω = natural frequency
• {ϕ} = mode shape (eigenvector)
This formulation yields eigenvalues (natural frequencies squared) and eigenvectors (mode shapes).
Detailed Explanation
In mathematical terms, the behavior of a dynamic system under free vibration can be expressed using matrices that represent mass and stiffness. By assuming a specific form of vibration (harmonic), we can derive an eigenvalue problem that helps us find the natural frequencies and the corresponding mode shapes of the structure. The eigenvalues tell us the frequencies at which the system naturally vibrates, while the eigenvectors give us the associated mode shapes.
Examples & Analogies
Think of tuning forks. Each fork vibrates at its own frequency when struck. By analyzing the vibrations (like we analyze the eigenvalues) of a fork, you can identify its unique musical note (or mode shape). This is similar to how structures can vibrate and how we can predict their response during an earthquake.
Properties of Mode Shapes - Orthogonality and Normalization
Chapter 4 of 8
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Mode shapes are orthogonal with respect to both the mass and stiffness matrices:
• Mass orthogonality:
{ϕ}^T[M]{ϕ}=0 for i≠j
• Stiffness orthogonality:
{ϕ}^T[K]{ϕ}=0 for i≠j
Orthogonality is key in modal superposition and decoupling the equations of motion.
Mode shapes are not unique in magnitude. They can be normalized for analytical convenience:
• Mass normalization:
{ϕ}^T[M]{ϕ}=1
• Stiffness normalization:
{ϕ}^T[K]{ϕ}=ω²
Detailed Explanation
Orthogonality in mode shapes means that the mode shapes do not interfere with each other in the analysis of vibrations; they are independent. This independence is crucial when using modal analysis to simplify complex systems into manageable equations. Normalization is a technique used to adjust the mode shapes to a standard size, making calculations easier and more consistent.
Examples & Analogies
Consider a music band where each instrument plays its tune without overlapping with others. Each player (mode shape) knows their part so well that it doesn't affect the others (orthogonality). If every instrument plays in unison at the same volume (normalization), it creates a harmonious sound that is easy to understand and enjoy.
Computation of Mode Shapes
Chapter 5 of 8
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Mode shapes can be computed by solving the eigenvalue problem using:
• Analytical methods for small systems (e.g., 2-DOF, 3-DOF)
• Numerical methods for large systems using:
– Subspace iteration
– Lanczos algorithm
– Rayleigh-Ritz method
For high-rise or complex structures, software like SAP2000, ETABS, or ANSYS is commonly used.
Detailed Explanation
To calculate mode shapes, engineers can use various mathematical approaches. Small systems can often be handled with simpler analytical methods, while larger, more complex systems require numerical techniques to find solutions effectively. Specialized software tools have been developed to assist in these computations, which can handle the complexity of high-rise structures.
Examples & Analogies
Imagine solving a jigsaw puzzle. For smaller puzzles, you might be able to do it by hand easily, but for larger ones, you need to take a more systematic approach—maybe sorting pieces by color or shape. Similarly, engineers use simplified techniques or powerful software based on the size of the system they are working with.
Interpretation of Mode Shapes in Structural Dynamics
Chapter 6 of 8
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
15.5.1 First Mode Shape
• Usually involves global movement of the entire structure.
• Dominant in seismic analysis due to its lower frequency and higher participation.
15.5.2 Higher Mode Shapes
• Represent localized or complex motion.
• Become significant in irregular or tall structures.
• Often show curvatures, torsions, or out-of-phase displacements between different parts.
Detailed Explanation
The first mode shape generally describes how a structure behaves in its entirety during vibration. It has the lowest frequency, making it a crucial factor during seismic events. Higher mode shapes describe more complex motions and become important for structures that are not uniformly shaped or that sway in more than one way. Understanding how these modes work helps engineers assess a structure's stability and resilience.
Examples & Analogies
Think of a large balloon. When you shake it gently, the whole balloon moves together (first mode). If you shake it harder or at different points, various parts of the balloon might move in different ways, displaying more complex vibrations (higher modes). Understanding these movements helps ensure the balloon does not pop under too much pressure!
Significance in Earthquake Engineering
Chapter 7 of 8
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
• Seismic Response: Structures tend to vibrate in their natural modes during seismic excitation.
• Design Optimization: Identifying mode shapes helps in modifying geometry or stiffness to improve performance.
• Modal Participation Factor: Indicates how much each mode contributes to the overall response.
• Time History and Response Spectrum Analysis: Use mode shapes to determine maximum displacements and internal forces.
• Mode Combination Rules: Use of SRSS (Square Root of Sum of Squares) or CQC (Complete Quadratic Combination) for combining modal responses.
Detailed Explanation
Understanding the significance of mode shapes in earthquake engineering allows engineers to predict how a structure will behave during quakes. This knowledge can be used to refine designs to prevent failure. Various analytical methods are also employed to measure how much each mode influences the overall response of the structure under seismic loads, leading to more robust designs.
Examples & Analogies
Consider how a flexible tree sways in the wind. By understanding how it moves (mode shapes), you can strengthen its trunk or branches where needed (design optimization) to ensure it doesn't break. Just like that tree, we can optimize buildings based on their expected reactions to earthquakes.
Use in Structural Control and Retrofitting
Chapter 8 of 8
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
• Mode shapes help identify weak stories, soft floors, and critical joints.
• Used in design of tuned mass dampers (TMDs), base isolation systems, and retrofit schemes.
• Changes in mode shapes before and after retrofitting provide insight into structural improvement.
Detailed Explanation
Mode shapes play a critical role in evaluating existing structures. Engineers can determine weaknesses in design and propose retrofitting solutions based on how a structure resonates during events like earthquakes. By analyzing the mode shapes before and after implementing these solutions, we can gauge the effectiveness of the changes made.
Examples & Analogies
Imagine a person with a weak ankle who struggles to run. By understanding their movement and identifying where they trip (mode shapes), we can suggest exercises or braces (retrofitting) to help them run smoothly again without losing balance. This process of analysis and improvement can greatly enhance stability.
Key Concepts
-
Free Vibration: Oscillation occurring without external forces post-disturbance.
-
Eigenvalue Problem: Mathematical approach to find natural frequencies and mode shapes.
-
Orthogonality: Independence of mode shapes facilitating simplified dynamic analysis.
-
Normalization: Standardizing mode shape definitions for analytical consistency.
Examples & Applications
A 3-DOF shear building has three distinct mode shapes corresponding to its unique vibrational profiles.
A cantilever beam exhibits different mode shapes where the first mode has a single curvature while the second mode presents double curvature.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
When structures sway and shake, mode shapes are what they make.
Stories
Imagine a dance floor where dancers follow different moves. Each dancer represents a mode shape, moving independently but in harmony with the music's rhythm, the music being the forces acting on the structure.
Memory Tools
To remember the properties: 'O-N-C' - Orthogonality, Normalization, Computation.
Acronyms
M.A.P. - Mass, Analysis, Participation; the core components of assessing modal behavior.
Flash Cards
Glossary
- Mode Shape
The deformation pattern of a structure at a specific natural frequency during free vibration.
- Free Vibration
The vibration of a system without any external force after an initial disturbance.
- Natural Frequency
The frequency at which a system tends to oscillate in the absence of any driving force.
- Orthogonality
A property of mode shapes indicating that they are independent of one another in terms of their effects on the dynamic response.
- Eigenvalue Problem
A mathematical problem that involves finding eigenvalues and their corresponding eigenvectors for systems represented by matrices.
- Normalization
The process of scaling mode shapes to a standard magnitude for easier analysis.
Reference links
Supplementary resources to enhance your learning experience.
